Lepkość, tarcie wewnętrzne, cecha płynów, pojawienie się siły tarcia pomiędzy warstwami cieczy lub gazu, poruszającymi się równolegle względem siebie z różnymi co do wartości prędkościami. Warstwa poruszająca się szybciej działa przyspieszająco na warstwę poruszającą się wolniej i odwrotnie. Pojawiające się wtedy siły tarcia wewnętrznego skierowane są stycznie do powierzchni styku tych warstw.
Siła potrzebna do podtrzymania ruchu dwóch płytek względem siebie równoległych jest wprost proporcjonalna do powierzchni i prędkości, oraz odwrotnie do odległości między nimi i wynosi:
F=η(Sv/d).
Zjawisko lepkości wykazują wszystkie ciecze i gazy. Jedynym szczególnym wyjątkiem jest ciekły hel, który w temperaturach bliskich zera bezwzględnego wykazuje zjawisko nadciekłości czyli zupełne zniknięcie lepkości. Lepkość zależy w dużym stopniu od temperatury: dla cieczy zmniejsza się znacznie ze wzrostem temperatury, natomiast dla gazów nieco rośnie wraz z temperaturą.
Przepływ laminarny, opływ uwarstwiony, w którym poszczególne warstwy elementarne gazu lub cieczy nie mieszają się z sobą.
Siła oporu ruchu działająca ze strony cieczy na poruszającą się w niej kulkę wyraża wzór Stokesa
![]()
F= 6pηrv - dla nie ograniczonej ilości cieczy
-dla ruchu kulki wzdłuż cylindra o promieniu R F=
Siły działające na kulkę:
ciężkości F = m . g
wyporu Archimedesa Fw = mw g = g . ρ . V
siła oporu (Stokesa) Fo = Kv gdzie K = 6 . . . r . (1 + 2,4 . r/R)
Zgodnie z II zasadą dynamiki równanie ruchu kulki ma więc postać: ma=F-Fw-Fo lub
Jeżeli w chwili początkowej t=0 prędkośćv=v0, to po scałkowaniu dostajemy
zależność od czasu w postaci
![]()
gdzie nazywamy stałą czasową.
Prędkość graniczna kulki:
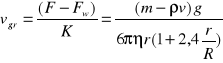
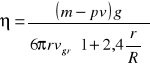
Wyznaczenie lepkości metodą Stokesa polega na bezpośrednim pomiarze wszystkich wielkości występujących po prawej stronie wzoru
![]()
![]()
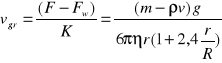
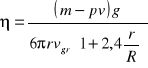
Wyszukiwarka
Podobne podstrony:
Konspekt na Fizykę, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 2 Wsp
Pomiar współczynnika lepkości2, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laborat
Lepkość2, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizyka
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[4]tabelka, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[8]konspekt new, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
FIZYK~47, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizyka
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
kospekt12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 Wyznaczanie
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
cw8 wyniki, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
mostek Wheatstone'a(1), Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, l
więcej podobnych podstron