Nr Ćwiczenia 2. |
Temat Ćwiczenia Współczynnik lepkości |
Ocena z Teorii |
|||
Nr Zespołu 2. |
Nazwisko i Imię Jarosław Radzik |
Ocena zaliczenia ćwiczenia |
|||
Data 04.03.13 |
Wydział EAIiIB |
Kierunek Elektrotechnika |
Rok 1 |
Grupa 5 |
Uwagi |
Konspekt do zajęć laboratoryjnych z Fizyki II
Cel ćwiczenia:
Zapoznanie się z własnościami cieczy lepkiej, wyznaczanie współczynnika lepkości metodą Stokesa.
Wprowadzenie:
Lepkość, tarcie wewnętrzne, wiskoza, cecha płynów, pojawienie się siły tarcia (tarcie) pomiędzy warstwami cieczy lub gazu, poruszającymi się równolegle względem siebie z różnymi co do wartości prędkościami. Warstwa poruszająca się szybciej działa przyspieszająco na warstwę poruszającą się wolniej i odwrotnie. Pojawiające się wtedy siły tarcia wewnętrznego skierowane są stycznie do powierzchni styku tych warstw.
Określana ilościowo współczynnikiem η równym wartości siły stycznej, która przyłożona do jednostki powierzchni spowoduje jednostajny, laminarny przepływ z jednostkową prędkością:
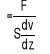
,
gdzie F/S - naprężenie ścinające, dv/dz - poprzeczny gradient prędkości.
Wzór powyższy podany już przez I. Newtona odnosi się do cieczy nieściśliwej.
W układzie CGS (Centymetr Gram Sekunda) jednostką lepkości jest puaz, w SI jest to niutonosekunda na metr kwadratowy [N⋅s/m2]. Współczynnik lepkości η wyznacza się wiskozymetrami. Oprócz powyżej określonej lepkości stosuje się pojęcia lepkości właściwej (stosunku lepkości danej cieczy do lepkości wody w temperaturze 0°C), lepkości względnej (lepkości danej cieczy względem lepkości wody w tej samej temperaturze).
Wielkość φ = 1/η nazywana jest płynnością. Dla polimerów i układów dyspersyjnych definiuje się pojęcie lepkości strukturalnej, opisującej powstawanie struktur w cieczy w zależności od prędkości przepływu.
Lepkość zależy w dużym stopniu od temperatury. Dla gazów rośnie proporcjonalnie do temperatury bezwzględnej. Dla cieczy zmniejsza się znacznie ze wzrostem temperatury. Bardzo silną zależność temperaturową obserwuje się dla cieczy o dużej lepkości jak np. dla gliceryny czy dla olejów silnikowych.
Jedynym wyjątkiem jest ciekły hel, w którym w temperaturze bliskiej 0K lepkość całkowicie zanika.
Przepływ laminarny, przepływ turbulentny, przepływ płynu (cieczy, gazu), w którym kolejne warstwy płynu nie ulegają mieszaniu (w odróżnieniu od przepływu turbulentnego, burzliwego).
Zachodzi, gdy liczba Reynoldsa nie przekracza tzw. wartości krytycznej. Przy przepływie laminarnym w rurze poprzeczny rozkład prędkości opisuje parabola.
Przepływ laminarny Przepływ turbulentny
Re<<1 (mała prędkość) Re>2000 (duża prędkość ciała)
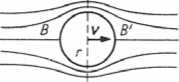
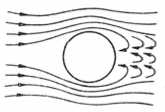
Ruch kulki w cieczy
Lepkość płynów (cieczy i gazów) jest odpowiedzialna za występowanie oporów ruchu ciała poruszającego się w płynie. Trajektorie cząstek cieczy wokół poruszającej się kulki są przykładem opływu laminarnego, występującego przy małych prędkościach, kiedy ciecz opływająca kulkę nie tworzy jeszcze żadnych wirów, czyli turbulencji. W analogii do wzoru na η siła oporu lepkiego działającego na dowolny przedmiot w zakresie opływu laminarnego jest proporcjonalna do współczynnika lepkości i prędkości kulki.
Prawo Stokesa, hydrodynamiczne prawo opisujące siłę oporu F towarzyszącą jednostajnemu ruchowi ciała zanurzonego w lepkim płynie, prawdziwe w przypadku małych liczb Reynoldsa charakteryzujących przepływ (Re<<1).
Zgodnie ze prawem Stokesa, siła ta, o zwrocie przeciwnym do zwrotu prędkości ciała, ma wartość określoną wzorem:
F = 6π·η·r·v,
gdzie: η - współczynnik lepkości dynamicznej cieczy (lepkość), r - promień ciała, u - prędkość ruchu ciała względem cieczy.
Jednostka współczynnika lepkości
Prawo Stokesa wykorzystuje się do określania prędkości sedymentacji cząstek i do wyznaczania lepkości cieczy (wiskozymetry).
Wzór ten jest słuszny, gdy kulka porusza się w nieograniczonej objętości cieczy. W przypadku, gdy ruch kulki odbywa się wzdłuż osi cylindra o promieniu R wzór ten przybiera postać:
![]()
Ruch kulki w cieczy:
Jeżeli kulka spada w cieczy pod wpływem grawitacji, działają na nią następujące trzy siły:
F = m·g - siła ciężkości,
Fw = mw·g = ρ·V·g - siła wyporu Archimedesa, gdzie ρ - gęstość cieczy, V - objętość kulki,
FO = K·v - stała oporu (siła Stokesa), gdzie K = 6π·η·r·v.
Zgodnie z II zasadą dynamiki równanie ruchu kulki ma postać:
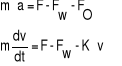
Jest to równanie różniczkowe pierwszego rzędu ze względu na prędkość v.
Jeżeli w chwili początkowej t = 0 prędkość v = v0 to po scałkowaniu dostajemy zależność prędkości od czasu w postaci:
![]()
gdzie wielkość τ = m/K nazywamy stałą czasową.
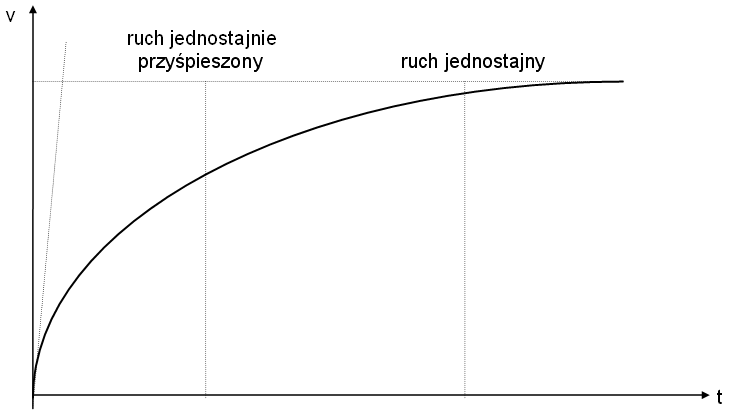
Drugi wyraz wzoru maleje ekspotencjalnie z czasem, więc dla dostatecznie dużego t jest on zaniedbywanie mały. Skutkiem tego ruchu kulki po czasie rzędu 3τ staje się jednostajny z prędkością graniczną równą:
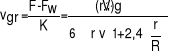
Pomiar prędkości spadania kulki w cieczy stanowi jedną z metod wyznaczania współczynnika lepkości cieczy. Droga jaką przebędzie kulka przed osiągnięciem prędkości granicznej wynosi około 3τvgr.
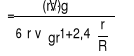
Wyznaczanie lepkości metodą Stokesa polega na bezpośrednim pomiarze wszystkich wielkości występujących po prawej stronie wzoru. Zamiast kul wykonanych z ciała stałego wykorzystać też można kuliste krople cieczy o większej gęstości, spadające w cieczy badanej.
Zakres stosowalności wzoru Stokesa
Wzór Stokesa jest słuszny tylko dla przepływów laminarnych. Parametrem, który decyduje o charakterze opływu cieczy wokół ciała jest liczba Reynoldsa, dana wzorem ogólnym:
![]()
,
gdzie ρ jest gęstością cieczy natomiast l oznacza wymiar liniowy poruszającego się ciała mierzony w kierunku prostopadłym do wektora v. W przypadku kulki przyjmujemy
l = 2r.
Liczba Reynoldsa wyraża stosunek sił bezwładności do sił lepkości. Stanowi kryterium przepływów laminarnych i turbulentnych, powyżej Re=2000 ruch laminarny płynu w przewodzie cylindrycznym przechodzi w ruch turbulentny.
Wyszukiwarka
Podobne podstrony:
moj projekt na kreski, Elektrotechnika AGH, Semestr II letni 2012-2013, Podstawy Mechaniki, Projekt
[8]konspekt new new, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
[8]konspekt new, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
konspekt nr8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fi
konspekt 8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizy
konspekt 9, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizy
konspekt Cw5, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 5,4 Badanie
[8]konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, lab
poziomy energetyczne konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laborato
konspekt3, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labor
[7]konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, lab
[6]konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, lab
konspekt 8 1str, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Konspekt07 forM.B, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labork
Konspekt05, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[9]konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, lab
przerwa energetyczna konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laborato
[4]konspekt, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, lab
więcej podobnych podstron