Imię i nazwisko:	Ćw. E6 Szeregowy rezonans elektryczny.
Kierunek i rok:	Ocena z kolokwium: ………………….. …………………... Data/podpis	Ocena ze sprawozdania: …………………... …………………... Data/podpis	Ocena końcowa: …………………... …………………... Data/podpis
Nazwisko prowadzącego zajęcia: .

Cel doświadczenia.

Zbadanie krzywych rezonansowych dla parametrów obwodu RLC.

Przebieg doświadczenia.

1. Poszukać wstępnie częstotliwości rezonansowej (ustawić na generatorze zakres 10 kHz) dla trzech różnych wartości pojemności i indukcyjności.

• dla pojemności w granicach od 0,01 do 0,05
  

• dla indukcyjności w granicach od 0,0 do 0,5 H.

2. Wyznaczyć przebieg krzywych rezonansowych badając zmiany zależności natężania prądu I w obwodzie w funkcji częstotliwości
   . Pomiary wykonać w zakresie od 20 do 50 Hz z krokiem co 2 Hz.

3. Wykonać czynności dokładanie jak w punkcie 2 obciążając obwód trzema różnymi oporami omowymi w zakresie od 0,5 do 4,0
   .

Teoria.

Opór omowy.

Prawo Ohma mówi, że stosunek napięcia do natężania prądu jest stały i zależy tylko od właściwości przewodnika. Mamy zatem
.

Reaktancja lub opór bierny to wielkość charakteryzująca obwód elektryczny zawierający kondensator (pojemność) lub cewkę (indukcyjność). Jednostką reaktancji jest
. Gdy przez cewkę lub kondensator płynie prąd przemienny, wtedy część energii magazynowana jest w polu, odpowiednio magnetycznym lub elektrycznym. Wywołuje to spadek napięcia wprost proporcjonalny do iloczynu prądu i reaktancji.

Reaktancja cewki (opór indukcyjny) ma znak dodatni i oblicza się ją ze wzoru:

X_L = jωL gdzie L to indukcyjność własna cewki, ω pulsacja, j - jednostka urojona.

Reaktancja kondensatora (opór pojemnościowy) ma znak ujemny i oblicza się ją ze wzoru:

C - pojemność kondensatora, ω - pulsacja, j - jednostka urojona.

Gdy operujemy wyłącznie na oporach biernych możemy pominąć jednostki urojone i podstawić w ich miejsce 1.

Indukcja elektromagnetyczna - zjawisko powstawania siły elektromotorycznej w przewodniku pod wpływem zmiennego pola magnetycznego lub ruchu przewodnika w polu magnetycznym.

Samoindukcja (indukcja własna) jest zjawiskiem elektromagnetycznym, szczególnym przypadkiem zjawiska indukcji elektromagnetycznej. Samoindukcja występuje, gdy siła elektromotoryczna wytwarzana jest w tym samym obwodzie, w którym płynie prąd powodujący indukcję. Następuje wówczas sprzężenie zwrotne. Samoindukcja powoduje zmniejszenie natężenia prądu zmiennego. Opór, który prąd napotyka na skutek działania samoindukcji określany jest potocznie mianem induktancji. Induktancja ta powoduje również przesunięcie fazowe płynącego prądu. Samoindukcja występuje przede wszystkim w cewkach.

Prądy.

• Przemienny- średnie natężanie prądu nie zmienia się czasie. Wartości chwilowe natężenia prądu przyjmują naprzemiennie wartości dodatnie i ujemne.

• Zmienny- natężanie ulega zmianie w czasie t.

• Przemienny + zmienny = zmienny- natężenia i napięcie zmieniają się w czasie. Zmiany te zależą sinusoidalnie od czasu zmieniając kierunek przepływu.

• Prąd stały. Jeżeli zarówno natężanie jak i jego kierunek nie ulegają zmianie z biegiem czasu, to taki prąd nazywamy prądem stałym.

Obwód drgający.

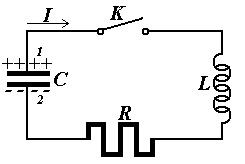
Dla odcinka 1LR2 obwodu mamy
gdzie I,
, E odpowiednio oznaczają wartości chwilowe. Natężenia prądu, różnicy potencjałów między okładkami 1 i 2 kondensatora oraz SEM.

W części 1LR2 działa jedynie SEM samoindukcji, wzbudzona w cewce w wyniku przepływu przez nią prądu zmiennego. Stąd
, a zatem można zapisać
Ładunek na okładce kondensatora to q zatem
oraz
. Różnica potencjałów na okładkach kondensatora
. Podstawiając do w wzoru
otrzymamy
W tym równaniu widać analogie do równania różniczkowego swobodnych drgań tłumionych ciężarka zawieszonego na sprężynie
Gdzie analogiem masy m jest indukcyjność L, współczynnik oporu

r to opór elektryczny R obwodu, a współczynnik sprężystości a jest odpowiednikiem odwrotności pojemności elektrycznej. Rozwiązaniem tego równania jest
gdzie
. Zastępując odpowiednio
,
,
(a= 1/C, m= L i r= R), otrzymamy
i jest to częstotliwość drgań własnych tego obwodu. Wynika stąd, że przy włączaniu naładowanego kondensatora w obwód składającego się z indukcyjności i oporu elektrycznego, połączonych szeregowo, ładunek q na okładkach kondensatora wykonuje drgania tłumione. Dlatego taki obwód nazywamy obwodem drgającym. Gdzie
jest tak zwanym współczynnikiem tłumienia.

Warunek rezonansu napięć.

W obwodzie w którym powstają drgania elektromagnetyczne, przy czym, jeśli obwód ten posiada opór będę to drgania tłumione. Drgania takie nie zasilane z zewnątrz będą stopniowo wygasały wskutek zużycia energii elektromagnetycznej na ciepło Joule'a. To taki obwód spełnia warunek rezonansu napięć który jest opisany wzorem




.

Zawada (impedancja lub opór pozorny)- stanowi wektorową sumę oporów. W tym oporu czynnego (omowego) R, indukcyjnego
, oraz pojemnościowego

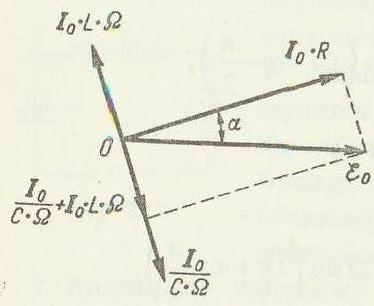
Jak widać z rysunku można wyznaczyć impedancje obwodu czyli opór całkowity obwodu.

oraz

Dobroć obwodu rezonansowego- jest to stosunek pulsacji rezonansowej
( równej
)

do podwójnego współczynnika tłumienia drgań elektromagnetycznych
obwodu nosi nazwę dobroci Q tego obwodu. Przejawia się wzorem
Gdzie
, a

Obliczenia.

1. Tabela przedstawiająca wyniki dotyczące punktu pierwszego przebiegu doświadczenia.

L.p.	L [Ω]	C [Ω]	I [mA]	ν [kHz]	R [Ω]
1	0,1	0,01	0,75	4100	1500
2	0,5	0,05	0,8	1000
3	0,9	0,09	0,6	510

2. Tabela przedstawiająca wyniki dotyczące punktu drugiego przebiegu doświadczenia.

L.p.
1	10,00	0,20
2	9,50	0,25
3	9,00	0,27
4	8,50	0,30
5	8,00	0,35
6	7,50	0,40
7	7,00	0,50
8	6,50	0,60
9	6,00	0,75
10	5,50	0,90
11	5,00	1,05
12	4,50	1,10
13	4,00	0,95
14	3,50	0,75
15	3,00	0,55
16	2,50	0,40
17	2,00	0,30
18	1,50	0,20
19	1,00	0,10

Wartości napięcia i oporu były stałe. Wynosiły odpowiednio:

3. Tabela przedstawiająca wyniki dotyczące punktu trzeciego przebiegu doświadczenia.

L.p.	ν [kHz]	I [mA]	R [Ω]		L.p.	ν [kHz]	I [mA]	R [Ω]
1	10,00	0,18	2500		1	10,00	0,18	3500
2	9,50	0,20				2	9,50		0,22
3	9,00	0,25				3	9,00		0,24
4	8,50	0,29				4	8,50		0,25
5	8,00	0,32				5	8,00		0,29
6	7,50	0,37				6	7,50		0,32
7	7,00	0,41				7	7,00		0,35
8	6,50	0,47				8	6,50		0,38
9	6,00	0,55				9	6,00		0,42
10	5,50	0,60				10	5,50		0,45
11	5,00	0,65				11	5,00		0,46
12	4,50	0,70				12	4,50		0,47
13	4,00	0,64				13	4,00		0,45
14	3,50	0,55				14	3,50		0,42
15	3,00	0,45				15	3,00		0,37
16	2,50	0,36				16	2,50		0,31
17	2,00	0,26				17	2,00		0,25
18	1,50	0,19				18	1,50		0,17
19	1,00	0,11				19	1,00		0,11

L.p.	ν [kHz]	I [mA]	R [Ω]
1	10,00	0,17	4500
2	9,50	0,19
3	9,00	0,21
4	8,50	0,25
5	8,00	0,28
6	7,50	0,28
7	7,00	0,30
8	6,50	0,32
9	6,00	0,34
10	5,50	0,35
11	5,00	0,36
12	4,50	0,37
13	4,00	0,36
14	3,50	0,35
15	3,00	0,32
16	2,50	0,27
17	2,00	0,22
18	1,50	0,17
19	1,00	0,11

Obliczam wartość dobroci obwodu rezonansowego dla poszczególnych wartości R.

Wartość tą obliczam z wzoru

Przy czym L oraz C są stałymi:

Dla
.

Dla
.

Dla
.

• Sporządzam dwa wykresy zależności
  w celu wykreślenia krzywych rezonansowych .Pierwszy wykres dotyczy punktu pierwszego (ogólny dla jednego typu pomiarów), a drugi punktu drugiego (dla trzech różnych oporów).

Wnioski.

Na podstawie dokonanych przeze mnie pomiarów i obliczeń sporządziłem wykres
dla trzech różnych oporów
,
,
. Na podstawie tych wykresów mogę stwierdzić że dla stałego napięcia
i przy stałych wartościach

L i C (

), maksymalna częstotliwość rezonansowa zawsze wynosi
i nie zmienia się pod wpływem oporu obciążającego obwód. Ponad to widać że wykresy zależności
są parabolami z ramionami skierowanymi ku dołowi. A wartości minimalne częstotliwości wszystkich trzech wykresów są takie same i wynoszą odpowiednio
i
.

W doświadczeniu miałem także wyznaczyć dobroć obwodu rezonansowego dla poszczególnych serii obliczeń. Otrzymałem następujące wyniki.

Dla
.

Dla
.

Dla
.

Dokonałem pomiaru dla trzech różnych oporów:

Przy czym wartości L oraz C są wartościami stałymi wynoszące odpowiednio:

Dla takich wartości będę obliczał wartość dobroci obwodu rezonansowego z wzoru

---