I Pracownia Zakładu Fizyki PL

Nazwisko i imię							Wydział ZiM 3,5 Grupa
Data 17,11,98 wyk. ćwicz		Numer ćwicz 3,1			Temat Wyznaczanie modułu Younga metodą jednostronnego rozciągania
Zaliczenie		Ocena	Data		Podpis

Zestawienie wyników w tabeli:

Lp	∆l [mm] zwiększanie	∆l [mm] zmniejszanie	P [N]
10	0,00	0,00	12,23
9	0,24	0,25	10,88
8	0,08	0,08	12,23
7	0,06	0,04	10,78
6	0,04	0,04	10,58
5	0,05	0,04	11,90
4	0,04	0,04	11,40
3	0,03	0,02	9,54
2	0,03	0,02	10,58
1	0,02	0,02	10,39

Lp	d [mm]
	2,07
	2,07
	2,06
	2,06
	2,06
	2,07
	2,06
	2,05
	2,06
	2,05
	2,06
	2,05
	2,05
	2,06
	2,04
śr	0,002058m

Podstawy teoretyczne:

Przy wyznaczaniu modułu Younga korzystamy z prawa Hooke`a wyrażającego się wzorem:

uwzględniając, że:

można zapisać:

σ = E*ε

Aby wyznaczyć moduł Younga dla danego materiału, należy więc dokonać pomiaru wartości odkształceń względnych ε i odpowiadających im naprężeń σ przy jednoosiowym rozciąganiu lub ściskaniu pręta.

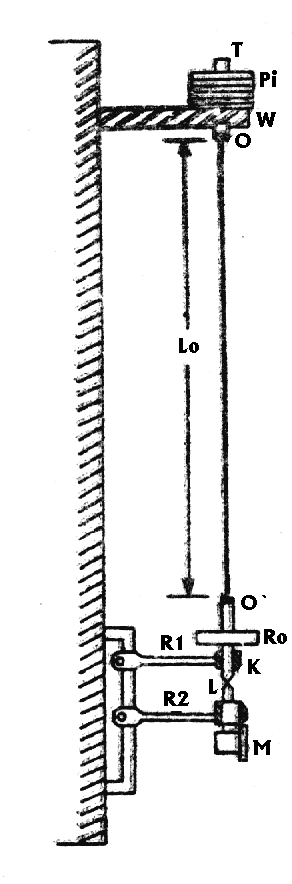
Do wykonania potrzebny jest przyrząd przedstawiony na rysunku. Badany pręt zamocowany jest jednym końcem w specjalnym uchwycie O, przytwierdzonym do sztywnego wspornika stalowego umocowanego w ścianie. Na jego dolnym końcu zamocowany jest element P_o, na który nakłada się ciężarki P_i i którego ciężar własny stanowi wstępne obciążenie usuwające różne rodzaje zgięć i zakrzywień pręta. Ramię R₁ służy do osiowego ustawiania elementu P_o i zabezpiecza pręt przed wychyleniem od pionu. Do ramienia R₂ zamocowany jest mikromierz M, służący do pomiaru wydłużenia ∆l. Na wsporniku W znajduje się trzpień T, na którym nałożone są obciążniki P_i.

Wykonanie ćwiczenia:

Po zamocowaniu drutu w uchwycie O i elemencie P_o mikromierz M ustawiamy tak, aby jego ruchomy trzpień L dotykał do końca K elementu P_o, następnie przymiarem liniowym dokonujemy pomiaru długości początkowej pręta l_o pomiędzy punktem O i O`. Po wyzerowaniu skali mikromierza, należy zdjąć pierwszy odważnik P₁ z trzpienia T i umieścić go na elemencie P_o. następnie należy dokonać odczytu wskazania mikromierza (tzn. określić wydłużenie ∆l). Z resztą odważników postępujemy tak samo. Następnie powtarza się czynności pomiarowe przy zdejmowaniu odważników. Po zakończeniu za pomocą śruby mikrometrycznej mierzymy średnicę pręta w kilku miejscach (15-200. Na podstawie tych wartości określa się średnią wartość średnicy pręta.

Opracowanie wyników:

Seria	Nr pomiaru	P [N]	∆l [m]*10^-3	Io [m]	S [m]*10^-6	σ [Pa]	εi 10^-3	E [N/m^2]	Ē [N/m^2]
Zwiększanie obciążenia	0	12,23	0,00	0,8	3,3264	3676647	0,000	-----------------	76735860590
		1	10,88			0,24				3270803	0,3	10902677569
		2	12,23			0,08				3676647	0,1	36766474266
		3	10,78			0,06				3240740	0,075	43209876543
		4	10,58			0,04				3180612	0,05	63612313612
		5	11,90			0,05				3577441	0,0625	57239057239
		6	11,40			0,04				3427128	0,05	68542568542
		7	9,54			0,03				2867965	0,0375	76479076479
		8	10,58			0,03				3180615	0,0375	84816418149
		9	10,39			0,02				3123496	0,025	124939874940
	Zmniejszanie obciążenia	0	12,23			0,00				3676647	0,000	-------------------
		1	10,88			0,25				3270803	0,3125	10466570466
		2	12,23			0,08				3676647	0,1	36766474266
		3	10,78			0,04				3240740	0,05	64814814814
		4	10,58			0,04				3180612	0,05	63612313612
		5	11,90			0,04				3577441	0,05	71548821548
		6	11,40			0,04				3427128	0,05	68542568542
		7	9,54			0,02				2867965	0,025	114718614719
		8	10,58			0,02				3180615	0,025	127224627225
		9	10,39			0,02				3123496	0,025	124939874940

Pomiary pierwsze przy zwiększaniu im zmniejszaniu obciążenia uznaję za błędy grube i nie uwzględniam ich przy dalszych obliczeniach.

Wielkość pola poprzecznego przekroju pręta obliczamy z zależności:

Naprężenie σ_i wyliczamy dla każdego pomiaru ze wzoru:

natomiast odkształcenie względne obliczamy wg jego definicji:

Na podstawie obliczonych wartości σ_i i ε_i wykonujemy wykres σ = f(ε), który zgodnie ze wzorem σ = E*ε (E = const) ma charakter liniowej zależności.

Praktyczna prosta najczęściej nie przebiega przez środek układu współrzędnych. tak więc rzeczywista prosta będzie miała postać

σ = b + E*ε

Wielkości b i E można wyznaczyć, biorąc pod uwagę dwie pary współczynników: na początku prostej, gdzie obciążenie ma wartość minimalną i na końcu prostej , gdzie obciążenie jest maksymalne.

po elementarnych przekształceniach otrzymujemy:

Opracowanie błędu metodą różniczkową:

Ostatecznie bezwzględny błąd maksymalny wynosi:

Wnioski:

Ćwiczenie jest łatwe do wykonania ale duży błąd wynika z jakości drutu użytego do ćwiczenia (duża grubość druta z wieloma załamaniami).

1

---