Fizyczne podstawy promieniowania rentgenowskiego i jego oddziaływanie z materią
Wiadomo, że promieniowanie elektromagnetyczne powstaje w wyniku niejednostajnego ruchu ładunku. Energia kwantu promieniowania wiąże się z długością fali oraz częstotliwością charakteryzującą kwant wzorem:
E = h · c ·
= h · c /
gdzie:
h - stała Plancka ( = 6.63 ·10-34 J· sec )
c - prędkość światła (= 3.0 · 10-8 m/sec)
częstotliwość promieniowania
- długość fali.
Promienie rentgenowskie (zwane także promieniami X) jest to promieniowanie elektromagnetyczne o długościach fali zawierających się w granicach od 0.0001 nm do 100 nm. Powstaje ono najczęściej w wyniku hamowania rozpędzonych w silnym polu elektrycznym elektronów.
Otrzymywanie promieniowania rentgenowskiego Typowe źródło promieniowania (lampa rentgenowska ) składa się z bańki próżniowej, wewnątrz której znajduje się katoda oraz anoda zwana również antykatodą (Rys.1). Rozżarzona katoda emituje elektrony. Pomiędzy katodą i anodą przykładane jest napięcie rzędu kilkudziesięciu tysięcy woltów.
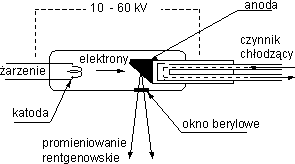
Rys.1. Otrzymywanie promieniowania rentgenowskiego.
Rozpędzone wysokim napięciem elektrony uderzając w materiał antykatody wytracają energię w dwojaki sposób:
W wyniku oddziaływania z jądrem atomu. Elektrony wiązki w różny sposób wytracają swoją energię, co prowadzi do powstania widma o różnych długościach fal. W ten sposób powstaje widmo ciągłe, zwane również promieniowaniem hamowania albo widmem białym. Maksymalna energia kwantu promieniowania odpowiada energii kinetycznej elektronu, ta zaś równa jest iloczynowi napięcia przyśpieszającego oraz ładunku elektronu:
Emax= e · U
Maksymalnej energii kwantu odpowiada fala o najmniejszej długości
min nazywana krótkofalową granicą promieniowania rentgenowskiego.
min = h·c / Emax = h · c / e · U = 1.239 / U
jeśli wyrazimy w [nm], zaś U w [kV].
W wyniku oddziaływania z elektronami atomów anody, przy odpowiednio dużej energii padającego elektronu, następuje wzbudzenie atomu, tj. przeniesienia elektronu atomu na wyższe poziomy energetyczne. W wyniku powrotu elektronu na niższy poziom energetyczny wytwarzane jest promieniowanie o ściśle określonej energii - powstaje widmo monochromatyczne. Długości fali tego promieniowania odpowiada iloczynowi stałej Plancka i prędkości światła podzielonej przez różnicę energii tych poziomów.
= h ·c / ( E2 - E1 )
Stwierdzono, że długości te jednoznacznie związane są z materiałem anody (odzwierciedlają strukturę powłoki elektronowej danego atomu), stąd widmo to nazywa się widmem charakterystycznym.
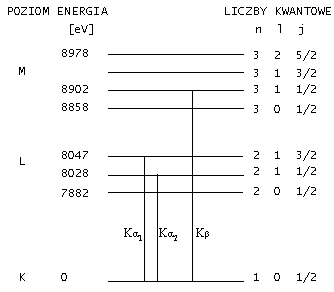
Poziomy energetyczne atomu przyjęto oznaczać literami alfabetu poczynając od litery K, którą oznaczono poziom najniższy. Również linie widma rentgenowskiego oznacza się zgodnie z nazwą poziomu, na który spada wzbudzony elektron, dodając wskaźniki zależne od poziomu z którego nastąpił przeskok. Jeśli przeskok następuje z powłoki sąsiedniej to dodaje się wskaźnik jeśli z następnej to dodaje się wskaźnik , itd. Dodatkowo wprowadza się oznaczenia liczbowe dla rozróżnienia podpoziomów związanych z różnymi liczbami kwantowymi j.
Na Rys. 2. przedstawiono układ poziomów energetycznych atomu miedzi oraz pokazano schemat powstawania linii widmowych serii K.
Rys.2. Schemat poziomów energetycznych elektronów w miedzi
(rysunek wykonano bez uwzględnienia skali)
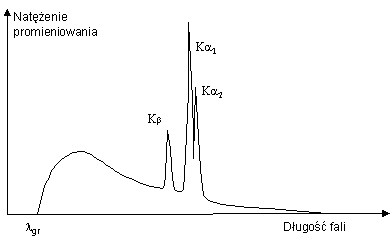
Typowe widmo promieniowania rentgenowskiego serii K przedstawione jest na Rys.3. Widoczne jest widmo ciągłe z krótkofalową granicą promieniowania min oraz widmo charakterystyczne K1, K 2, oraz K .
Rys.3. Przykładowe widmo promieniowania rentgenowskiego.
Elementy krystalografii
Krystalografia jest nauką o strukturze kryształów tj. ciał posiadających trójwymiarowe periodyczne uporządkowanie atomów, jonów lub molekuł, z których kryształ jest zbudowany. Ciała krystaliczne dzielą się na dwie grupy: 1) monokryształy, 2) polikryształy. Zwykle monokryształy kojarzą się jako ciała o dobrze wykształconych płaskich ścianach tworzących wielościany. Monokryształem może być również ciało nie mające widocznych, dobrze wykształconych ścian zewnętrznych. Jeżeli ciało składa się z drobnych elementów monokrystalicznych o nieregularnych kształtach zwanych ziarnami, które są ze sobą pozrastane, to wtedy mamy ciało polikrystaliczne. Monokryształy są ciałami jednorodnymi i anizotropowymi. Anizotropia oznacza, że własności fizyczne ciała zależą od określonego kierunku w krysztale, np. rozszerzalność termiczna kryształu w jednym kierunku różni się od rozszerzalności w kierunku doń prostopadłym. Polikryształy zwykle mają dowolną orientację ziaren i dlatego są ciałami izotropowymi. Jeżeli jednak w ciele polikrystalicznym ziarna mają jakiś wyróżniony kierunek (kierunki) to mówimy, że ciało polikrystaliczne ma teksturę i upodabnia się do monokryształu.
Sieć krystaliczna i sieć przestrzenna
Strukturę kryształu na rysunku można odwzorować w różny sposób, tutaj przedstawimy dwa. Można zrobić rysunek periodycznie powtarzających się elementów fizycznych (atomów, molekuł) kryształu i otrzymamy wtedy sieć krystaliczną. Taki rysunek jest jednak mało przejrzysty i dość uciążliwy do wykonania. Dla wygody każdy fizyczny element strukturalny zastępujemy umownym symbolem np. kropką. Otrzymujemy wtedy periodycznie powtarzający się zbiór punktów -węzłów tworzących sieć przestrzenną (rys.4).
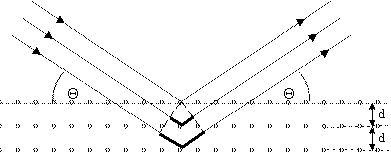
Dyfrakcja promieniowania rentgenowskiego Zgodnie z zasadą Huygensa każdy atom, do którego dociera promieniowanie staje się źródłem nowej fali. W pewnym przybliżeniu, układ atomów tworzących kryształ leżących w jednej dowolnej płaszczyźnie można potraktować jako płaszczyznę zwierciadlaną, od której odbija się wiązka promieniowania rentgenowskiego. Zgodnie z prawem odbicia, kąt odbicia równy jest kątowi padania - Q. Fale odbite od kolejnych, równoległych do siebie płaszczyzn sieciowych (zwanych rodziną płaszczyzn) interferują ze sobą dając w rezultacie wzmocnienie albo osłabienie wiązki. Wzmocnienie odbitego promieniowania wystąpi wówczas, kiedy różnica faz promieniowania odbitego od kolejnych płaszczyzn będzie wielokrotnością 2
. Ma to miejsce wówczas, kiedy różnica dróg przebytych przez kolejne fale (zaznaczona na rysunku linią pogrubioną) będzie równa wielokrotności długości fali padającego promieniowania -n
. Różnica ta wynosi 2d sin
(Rys. 5). Przyrównując obie wielkości otrzymujemy wzór wiążący długość fali, odległość między płaszczyznową oraz kąt, pod którym obserwujemy wzmocnienie:
n ·
= 2d sin
Wzór ten znany jest jako prawo Wulfa - Bragga, lub częściej jako prawo Bragga od nazwiska odkrywcy, który w roku 1913 jako pierwszy wykorzystał zjawisko dyfrakcji promieni Röntgena do badania struktury kryształów. G.W Bragg wraz z ojcem H.W. Braggiem za odkrycia te otrzymali w roku 1915 nagrodę Nobla.
Rys.5. Dyfrakcja promieni na układzie płaszczyzn sieciowych.
Wyszukiwarka
Podobne podstrony:
efekt comptona2, Akademia Morska Szczecin, SEMESTR II, Fizyka, sciaga fiza
w 06 promieniowanie - abso, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Czdosw1, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Pomiar siły elektromotorycznej ogniwa, Akademia Morska Szczecin, SEMESTR II, Fizyka, I semestr
Wyznaczanie temperatury Curie ferrytu [wnioski], Akademia Morska Szczecin, SEMESTR II, Fizyka, I sem
Fizyka-6, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
CZ DO WIADCZALN1, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Pomiar rezystancji metodą mostkową, Akademia Morska Szczecin, SEMESTR II, Fizyka, I semestr
w 02 Badanie rezonansu w o, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Cz do wiadczalna, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Wyznaczanie temperatury Curie ferrytu, Akademia Morska Szczecin, SEMESTR II, Fizyka, I semestr
DROGA I PRĘDKOŚĆ STATKU, Akademia Morska Szczecin, SEMESTR II, NAWIGACJA, wykłady II sem
POLE MAGNETYCZNE STATKU, Akademia Morska Szczecin, SEMESTR II, NAWIGACJA, wykłady II sem
Droga transportowa sciaga1, Akademia Morska Szczecin, SEMESTR II
więcej podobnych podstron