1. Sprawdź ortogonalność wektorów :
,

2. Co to jest gradient funkcji. Wykorzystując gradient funkcji, oblicz przyrost funkcji
po przesunięciu się z punktu
do punktu
.

3. Wyjaśnij pojęcia: Dywergencja i rotacja pola wektorowego oraz laplasjan pola skalarnego.

4. Co to jest pole potencjalne (pole o potencjale skalarnym)?

5. Co oznacza pojęcie „funkcje harmoniczne”? Czy potencjał grawitacyjny (uwzględniający siłę przyciągania i siłą odśrodkową) jest funkcją harmoniczną?

6. W punktach o współrzędnych

X1=0, X2=1000

Y1=0, Y2=1000

Z1=0, Z2=1000

Umieszczono masy punktowe
,
. Wyznacz potencjał grawitacyjny w punkcie P (Xp=5000, Yp=5000, Zp=5000) oraz wektor przyspieszenia.

.

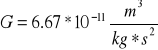
7. Co przedstawia równanie:

8. Wykazać, że wektor przyspieszenia g jest prostopadły do powierzchni ekwipotencjalnej W=const. W jaki sposób własność ta jest wykorzystywana w geodezji?

9. Omów równanie nr 1. Czym różni się ono od równania nr 2.

1.

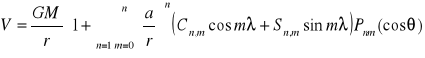
2.

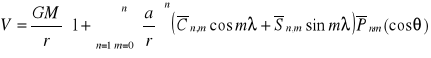
10. Wymień i krótko scharakteryzuj czynniki wywołujące zmiany pola grawitacyjnego Ziemi.

11. Co to jest potencjał zakłócający. Czy potencjał zakłócający jest funkcją harmoniczną?

12. Jaka jest różnica pomiędzy zakłóceniem grawimetrycznym a anomalią grawimetryczną. Przedstaw podstawowe równanie geodezji fizycznej.

13. W jaki sposób wyznaczamy anomalie Bouguera?

14. W jaki sposób można wyznaczyć wartość przyspieszenia pod powierzchnią terenu (np. na geoidzie), na podstawie przyspieszenia pomierzonego na powierzchni? Podaj przykład zastosowania takiej redukcji.

15. Omów ogólnie znane Ci hipotezy dotyczące zagadnienia izostazji.

16. Przedstaw zagadnienia brzegowe teorii potencjału oraz geodezyjne zagadnienia brzegowe.

17. Omów wzór:

Przy jakich założeniach wór ten jest ważny?

18. Omów różnice pomiędzy rozwiązaniem Stokesa i Mołodeńskiego.

19. Na czym polega technika usunięcia i odtworzenia w zagadnieniu wyznaczania geoidy i quasi-geoidy.

20. Na czym polegają względne i bezwzględne pomiary grawimetryczne. Przedstaw różnice pomiędzy grawimetrami statycznymi i dynamicznymi (podaj przykłady).

Pytania jakie były na egzaminie w I terminie

1. Znajć parametr k w wektorach
   ,
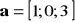
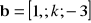
   które są ortomertyczne

2. a) Wyjaśnij pojęcia: Dywergencja i rotacja pola wektorowego oraz laplasjan pola skalarnego.

b) Co to jest pole potencjalne (pole o potencjale skalarnym)?

3. W punktach o współrzędnych

X1=0, X2=2000

Y1=0, Y2=2000

Z1=0, Z2=1000

Umieszczono masy punktowe
,
. Wyznacz potencjał grawitacyjny w punkcie P (Xp=1000, Yp=1000, Zp=2000) oraz wektor przyspieszenia.

.

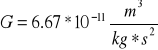
4. Omów równanie nr 1. Czym różni się ono od równania nr 2.

1.

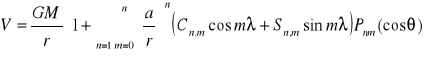
2.

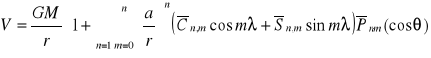
5. Co to jest potencjał zakłócający. Czy potencjał zakłócający jest funkcją harmoniczną?

6. Omów różnice pomiędzy rozwiązaniem Stokesa i Mołodeńskiego.

---