CAŁKI OZNACZONE:
WZÓR NEWTONA-LEIBNIZA:
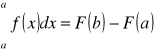
CAŁKOWANIE PRZEZ
CZĘŚCI: 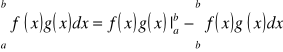
PODSTAWIANIE: 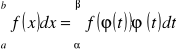
WŁASNOŚCI CAŁEK:
Jeśli f jest całkowalna na przedziale [a, b], a funkcja g różni się od funkcji f jedynie w skończonej liczbie punktów z przedziału [a, b], to g też jest całkowalna i
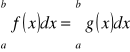
.Jeśli f jest całkowalna na [a, b], to:
Dla dowolnego
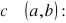
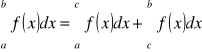
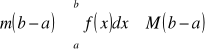
, gdzie m i M są dowolnymi liczbami, takimi że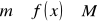
dla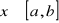
.
Jeżeli funkcje f i g są całkowalne na [a, b], to:
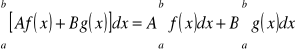
, dla dowolnych liczb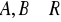
.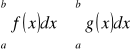
, gdy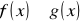
, dla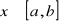
Pole figury:
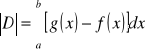
Wyszukiwarka
Podobne podstrony:
koło z matmy, Zarzadzanie Pwr, Semestr 1, Matematyka, Matematykaa, koło analiza 1 i 2. Porosiński 24
Calka oznaczoxna, Biotechnologia PWR, Semestr 2, Analiza Matematyczna 2, Notatki
CAŁKI OZNACZONE - wzory, Budo2 II, Matematyka
Matematyka-pochodne i zastosowanie, WSFiZ - Zarządzanie, II semestr, Matematyka, mgr Dorota Narojczy
dyskretna2, Studia, PWR, 2 semestr, Matematyka dyskretna
1 kolo - opracowaniej, Zarządzanie PWR, Semestr 6, Analiza finansowa wspomagana komputerem
dyskretna-przyklad-zadania-na-pierwsze-kolokwium, Studia, PWR, 2 semestr, Matematyka dyskretna, kolo
dyskretna-egzamin-zaoczne-szablon, Studia, PWR, 2 semestr, Matematyka dyskretna, kolokwium
dyskretna-egzamin-zaoczne, Studia, PWR, 2 semestr, Matematyka dyskretna, kolokwium
kolo 2-sc, Zarządzanie PWR, Semestr 6, Analiza finansowa wspomagana komputerem
kolo 2, Zarządzanie PWR, Semestr 6, Analiza finansowa wspomagana komputerem
plikus.pl zarzadzanie, PWR, semestr I, zarządzanie, zarządzanie ściągi
ćwiczenia-Rynkowa-ochrona-konsumentów-Tematy-do-kolokwium, Zarządzanie PWR, Semestr 4, ROK Rynkowa O
konkurencja doskonała i monopol, Zarządzanie PWr, I semestr, Mikroekonomia
więcej podobnych podstron