Zadanie 1

Zaprojektować fundament na palach pod ścianę budynku - warunki gruntowe jak na rys. 1

1. Założenia wstępne

Obciążenia charakterystyczne stałe i zmienne długotrwałe:

P_n = 340 kN/m

H_n = 10 kN/m

M_n = 10 kNm/m

Obciążenia obliczeniowe stałe, zmienne krótko- i długotrwałe oraz wyjątkowe:

P_r = 355 kN/m

H_r = 12 kN/m

M_r = 15 kNm/m

Przyjmuję do projektowania:

• beton ławy B 15 (γ_b⁽ⁿ⁾ = 24 kn/m³)

• stal A II, 18G2 (R_a = 310 MPa)

• pale prefabrykowane o średnicy 0,3 m.

2. Przyjęcie rozmieszczenia pali, wymiarów ławy, zestawienie obciążeń

Pale pod ławą rozmieszczono w dwóch rzędach (rys. 2). Osiowy rozstaw pali wynosi

r = 1,389 m. Rozstaw rzędów pali wynosi r₁ = 0,7 m, odstęp mierzony równolegle do długości ławy l₀ = 1,2 m. Wysokość ławy przyjęto h = 0,7 m.

Ponieważ na ławę działają stałe obciążenia planuje się przesunięcie środka ciężkości układu palowego względem osi ściany. Mimośród wypadkowej obciążeń obliczeniowych względem osi ściany w poziomie podstawy ławy wynosi:

e =
=0,066 m = 6,6 cm

Przyjmuję przesunięcie środka ciężkości układu palowego względem osi ściany o 6 cm.

Ciężar własny ławy (rys. 3):

- charakterystyczny

G_1n = 1,4⋅0,7⋅24,0 = 23,52 kN/m

- obliczeniowy

G_1r = 1,1⋅23,52 = 25,87 kN/m

Ciężar posadzki:

- charakterystyczny

G_2n = 0,495⋅0,15⋅24,0 = 1,78 kN/m

- obliczeniowy

G_2r = 1,3⋅1,78 = 2,32 kN/m

Ciężar gruntu nad odsadzką:

- charakterystyczny

G_3n = 0,395⋅0,8⋅1,7⋅9,81 = 5,27 kN/m

- obliczeniowy

G_3r = 1,2⋅5,27 = 6,32 kN/m

Mimośród wypadkowej obciążeń względem środka układu palowego:

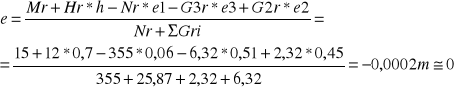
Ze względu na pomijalnie małą wartość mimośrodu zakładam, że wszystkie pale są jednakowo obciążone:

R_r = (N_r + G_1r + G_2r + G_3r)l₀ = (355 + 18,48 + 2,32 + 6,32)⋅1,2 = 458,54 kN

3. Przyjęcie długości i obliczenie nośności pala

Nośność pala powinna wynosić:

0,9*N_t ≥ R_r + G_rp + T_r (1)

, gdzie G_rp - ciężar własny pala.

Dla pali prefabrykowanych (tab. 5.7):

S_s = 1,1 dla piasków średnich, I_D = 0,49

S_s = 0,9 dla gliny pylastej zwięzłej, I_L = 0,4

S_s = 1,0 i S_p = 1,0 dla żwiru, I_D = 0,49

Pole podstawy pala (D = 0,3 m):

A_p = D²/4 = ⋅0,3²/4 = 0,071 m²

Ponieważ w podłożu występuje warstwa gruntu nienośnego, który będzie podlegał konsolidacji, trzeba uwzględnić możliwość pojawienia się tarcia ujemnego.

Przy wyznaczaniu współczynników t_i oraz q:

• dla warstwy I poziom 0,00 znajduje się w poziomie terenu,

• dla warstw III, IVa i IVb, na poziomie określonym przez h_z ponad stropem gliny:

Ps: γ' = 19,62/2 = 9,81 kN/m³

G_z: γ' = 18,64 - 9,81 = 8,83 kN/m³

h_z =
=2,34 m

Grubość obliczeniowych warstw h_i, przez które przechodzi pal oraz średnie głębokości zalegania, sąnastępujące:

Warstwa I: grubość 1,5 m, śr. głębokość zalegania 2,25 m

Warstwa II: grubość 0,8 m

Warstwa III: grubość 1,1 m, śr. głębokość zalegania 2,89 m

Warstwa IVa: grubość 1,56 m, śr. głębokość zalegania 4,22 m

Warstwa IVb: zalega poniżej głębokości 5 m.

3.1 Obliczenie współczynników t_i dla średnich głębokości zalegania warstw

Warstwa I, piaski średnie: I_D = 0,49 regresja tab. 5,6 => t₅ = 59,7 kPa,

dla średniej głębokości zalegania: t_I = t_2,25 = 59,7⋅2,25/5,0 = 26,87 kPa

Warstwa II, torf nieskonsolidowany tab. 5.3 => t_II = 10 kPa

Warstwa III, Glina pylasta zwięzła: I_L = 0,4 => t₅ = 30 kPa,

dla średniej głębokości zalegania: t_III = t_2,89 = 30⋅2,89/5,0 = 17,34 kPa

Warstwa IV, Żwir: I_D = 0,49 => t₅ = 90,95 kPa

IVa: t_IVa = t_4,22 = 90,94⋅4,22/5,0 = 76,75 kPa

IVb: t_IVb = t₅ = 90,94 kPa

3.2 Obliczenie współczynnika q

Średnica pala D = 0,3 m, więc

h_c =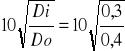
=8,66 m

Wstępnie zakładam, że podstawa pala będzie się znajdować w żwirach na głębokości mniejszej niż 8,66 m poniżej poziomu zastępczego.

I_D = 0,49 regresja tab. 5.5 => q₁₀ = 3988,24 kPa

Dla poziomu podstawy pala, oznaczając przez x zagłębienie pala w żwirach poniżej poziomu -5 m, mierzonego od poziomu zastępczego:

q_x = (5+x)q₁₀/10 = (5+x)⋅3988,24/10 = 398,824x + 1994,12

Powierzchnie boczne pala w obrębie poszczególnych warstw:

A_sI = ⋅D⋅h_I = ⋅0,3⋅1,5 = 1,414 m²

A_sII = ⋅0,3⋅0,8 = 0,754 m²

A_sIVa = ⋅0,3⋅1,56 = 1,47 m²

A_sIVb = 0,942x m²

3.3 Obliczenie wartości jednostkowych wytrzymałości q^(r) i t_i^(r)

• pod podstawą:

q^(r) = 0,89q_x = 354,95x + 1774,77

• na pobocznicy:

t_I^(r) = 1,16⋅26,87 = 34,29 kPa

t_II^(r) = 10 kPa

t_III^(r) = 0,84⋅17,34 = 14,57 kPa

t_IVa^(r) = 0,89⋅76,75 = 68,31 kPa

t_IVb^(r) = 0,89⋅90,94 = 80,94 kPa

3.4 Wyznaczenie długości pala (p. rys. 4)

l_p = 6,46 + x - 1,5 = 4,96 + x

Ciężar obliczeniowy pala:

G_rp = D²/4 ⋅γ_f⋅l_p⋅γ_b = ⋅0,3²/4 ⋅1,1⋅(4,96+x)⋅24,0 = 1,866x+9,256

Wypadkowa ujemnego tarcia gruntu

T_r = S_sI⋅A_sI⋅t_I^(r) + A_sII⋅t_II^(r) = 1,1⋅1,414⋅34,29 + 0,754⋅10 = 60,87 kPa

Z równania (1) otrzymuję wartość x (zał.: m₁ = 1):

0,9⋅(S_p⋅q^(r)⋅A_p + m₁⋅S_si⋅t_i^(r)⋅A_si) ≥ R_r + G_rp + T_r

0,9[1,0⋅(354,95x+1774,77)⋅0,071 + 1,0⋅(0,9⋅14,57⋅1,037 + 1,0⋅68,31⋅1,47 + 1,0⋅80,94⋅0,942x)] = 458,54 + 1,866x + 9,256 + 60,87 => x = 3,496 m

Obliczona długość pala: l_p = 6,46 + 3,5 - 1,5 = 8,46 m, przyjęto l_p = 8,50 m

3.5 Sprawdzenie nośności pala w grupie

Promień podstawy strefy naprężeń:

R = D/2 + h_i⋅tg _i = 0,3/2 + 1,1⋅0,07 + (3,5 + 1,56)⋅0,105 = 0,758 m

Osiowy rozstaw pali: r = 1,389 m

r/R = 1,389/0,758 = 1,83 tab. 5.4 => m₁ = 1

Strefy naprężeń na siebie nie zachodzą, nośność pala jest więc równa nośności pala pojedynczego. Przyjęta długość pala jest zatem wystarczająca.

4. Wymiarowanie ławy

4.1 Zbrojenie poprzeczne ławy (p. rys. 5)

₂ > ₁ = 33,69° > 30° => ława wysoka.

Obliczeniowa siła rozciągająca zbrojenie, wynikająca z oddziaływania pala na ławę:

Z =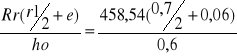
313,34 kN

Potrzebna ilość zbrojenia:

F_a = Z/R_a = 313,34/310e3 = 0,001m² = 10 cm²

Przyjmuję 5  16, F_a = 10,05 cm². Pręty należy rozmieścić w paśmie nad palem o szerokości 2D = 2⋅0,3 = 0,6 m, a więc co 15 cm.

4.2. Zbrojenie podłużne ławy

Ciężar własny ławy, gruntu nad odsadzką i posadzki:

G_r = G_1r + G_2r + G_3r = 25,87 + 2,32 + 6,32 = 34,51 kN/m

Ciężar pryzmy trójkątnej muru:

P_r = γ_f⋅l₀⋅tg 60°⋅a⋅γ^(n_muru = 1,1⋅1,2⋅1,73⋅0,51⋅18,0 = 20,96 kN/m

P_r + G_r = 20,96 + 34,51 = 55,47 kN/m

l = 2l₀ = 2⋅1,2 = 2,4 m

M₁ = 55,47⋅2,4²/9 = 35,5 kNm

M₂ = 55,47⋅2,4²/14 = 22,82 kNm

M₃ = 55,47⋅2,4²/11 = 29,05 kNm

Dla wyznaczonych momentów, przekroju ławy, klasy betonu i stali wyznacza się potrzebny przekrój zbrojenia.

A₀ =
=0,0081 =>  = 0,995,  = 0,01, r₀ = 10,0

F_a =
= 0,000192 m² = 1,92 cm² < F_{a min}

, przyjmuję więc: F_{a min} = b⋅h⋅_min = 140⋅70⋅0,0015 = 14,7 cm²

Przyjęto zbrojenie górą i dołem po 6  18 prętów (F_a = 15,27 cm²) 18G2 rozmieszczone równomiernie na całej szerokości ławy.

5. Osiadanie pala pojedynczego (P_n = 340 kN/m)

Charakterystyczne obciążenie przekazywane z fundamentu na pal:

Q_nF = (340 + 23,52 + 1,78 + 5,27)⋅1,2 = 444,68 kN

Charakterystyczny ciężar własny jednego pala:

G_4n = 8,8⋅⋅0,3²⋅0,25⋅24,0 = 14,42 kN

Charakterystyczny ciężar pala w obrębie piasków:

G'_4n = 1,5⋅⋅0,3²⋅0,25⋅24,0 = 2,54 kN

Charakterystyczne obciążenie pala T⁽ⁿ⁾ od tarcia ujemnego:

tab. 5.3 => t^(r) = 10 kPa, T⁽ⁿ⁾ = ⋅D⋅h_I⋅t^(r)/γ_m = ⋅0,3⋅1,5⋅10/1,16 = 12,85 kN

Moduł odkształcenia gruntu dla gruntów uwarstwionych można przyjąć jako średnią ważoną modułów odkształcenia wzdłuż trzonu pala, przyjmując jako wagę miąższość poszczególnych warstw.

Warstwa II torf nieskonsolidowany, przyjmuję E_0II = 5000 kPa

Warstwa III glina pylasta zwięzła, E_0III = 18000 kPa, 18000⋅0,9 = 15120 kPa

Warstwa IV żwir, E_0III = 138000, 138000⋅0,9 = 122820 kPa

Średni moduł dla podłoża gruntowego otaczającego pal:

E₀ =
=92431 kPa

Moduł E_b poniżej podstawy:

E_b = 138000⋅1,0 = 138000

W rozpatrywanym przypadku osiadanie pala należy obliczać jako sumę osiadania pala w gruncie nośnym, tj. poniżej stropu torfu z uwzględnieniem pali sąsiednich i skrócenia pala na odcinku, gdzie występuje tarcie ujemne. Przyjmuję obciążenie Q_n = Q_nF + G_4n + T⁽ⁿ⁾. Skrócenie pala na odcinku warstwy I oblicza się jak dla pręta ściskanego obciążonego siłą przekazywaną z fundamentu i połową (T⁽ⁿ⁾ + G'_4n)⋅G'_4n - ciężar pala w obrębie warstwy I.

Osiadanie pala od obciążenia Q_n:

s =
, I_w = I_OK⋅R_b

h = 0,8 + 1,1 + 5,1 = 7,0 m

=7/0,3 ≈ 25

=138000/92431 = 1,33

R_a = 1,0, K_A =
⋅R_A = 27e6/92431⋅1 = 292

tab. 6.3 => R_b = 0,9, tab. 6.1 => I_OK. = 3,3,

I_W = 3,3⋅0,9 = 2,97

Osiadania pojedynczego pala w przyjętych do obliczeń warunkach gruntowych dla jednostkowej siły Q_n:

s₁ = 1⋅2,97/(7⋅92431) = 4,59⋅10^-6 m

Osiadanie pala od siły Q_n:

s = 4,59e-6⋅471,95 = 0,22 cm

Osiadanie dowolnego pala i pod ławą:

s_i = s_1i⋅Q_ni + s_ij⋅Q_nj⋅_ij⁰, dla i ≠ j

_ij⁰ = ⁰_F - F_E(⁰_F - ⁰_E)

Obliczenie osiadania pala nr 1 z uwzględnieniem pali 2 ÷ 7 (p. rys. 6):

Numer pala	r [m]	r/D (D/r)	KA	h/D	^0F	^0E	FE	^0ij
2	2,4	0,125	292	23,33333	0,3	0,07	0,04	0,2908
3	2,4	0,125	292	23,33333	0,3	0,07	0,04	0,2908
4	1,389	4,63	292	23,33333	0,33	0,09	0,04	0,3204
5	1,389	4,63	292	23,33333	0,33	0,09	0,04	0,3204
6	3,667	0,081811	292	23,33333	0,17	0,01	0,04	0,1636
7	3,667	0,081811	292	23,33333	0,17	0,01	0,04	0,1636

Osiadanie pala nr 1 w gruncie nośnym wynosi:

s₁ = 0,00217 + 0,00217(2⋅0,2908 + 2⋅0,3204 + 2⋅0,1636) = 0,55 cm

Skrócenie pala w obrębie gruntów nienośnych:

_s =
=0,036 cm

Całkowite osiadanie pala:

s_c = s + _s = 0,00553263 + 0,000356 = 0,005888 m ≈ 0,59 cm