Państwowa Wyższa Szkoła Zawodowa w Krośnie Instytut Politechniczny
Laboratorium Mechaniki Płynów
Prowadzący:		Data wyk. ćw.
	Nr indeksu:	Ocena	Ocena
		Specjalność:	Grupa

Protokół z ćwiczenia nr 4

1. Temat ćwiczenia: Wyznaczanie współczynników strat lokalnych energii ζ przy przepływie cieczy w układzie hydraulicznym.

2. Cel ćwiczenia

Celem ćwiczenia jest doświadczalne wyznaczenie współczynników strat lokalnych ζ dla kolanka i załamania przewodu, gwałtownego zwężenia i rozszerzenia.

3. Podstawy teoretyczne

Miejscowe (lokalne) opory przepływu w przewodzie powodowane są przez innego rodzaju przeszkody (kolanka, załamania, gwałtowne zmiany przekroju przewodu, dyfuzory i konfuzory, zasuwy, przepustnice, zawory itp.), znajdujące się na drodze przepływającego strumienia. Opory te powstają wskutek zmian prędkości oraz występowanie obszarów wirowych. Na pokonanie lokalnych oporów przepływu tracona jest pewna część energii mechanicznej strumienia, która nosi nazwę lokalnych strat energii.

Do wyznaczania praktycznego strat lokalnych energii stosowane są większości równania empiryczne lub tablice i wykresy. Przyjmuje się, że straty lokalne są proporcjonalne do wysokości prędkości przepływu w przewodzie. W tych przypadkach, kiedy prędkości strumienia przed przeszkodą i za nią są różne, to straty energii mogą być wyznaczone przez wysokość obu tych prędkości.

Wysokość strat miejscowych h_m możemy więc wyrazić wzorem:

gdzie:

v₁ - średnia prędkość przepływu w przekroju przed przeszkodą,

v₂ - za przeszkodą,

ζ′ i ζ - współczynniki strat lokalnych w odniesieniu do odpowiednich prędkości.

Praktycznie współczynnik strat lokalnych najczęściej określamy w stosunku do prędkości poza przeszkodą.

Wielkości ζ zależą od rodzaju miejscowej przeszkody, liczby Reynoldsa Re i w pewnym stopniu od chropowatości ścian, a dla urządzeń dławiących jak przepustnice, zawory i inne - od stopnia ich otwarcia. Ze względu na bardzo złożony charakter zjawisk zachodzących przy przepływie przez miejscowe przeszkody, tylko w nielicznych przypadkach współczynnik ζ może być określony teoretycznie. W większości przypadków określa go się na drodze doświadczalnej. W świetle badań okazuje się, że współczynnik ζ najmocniej zależy od Re dla przepływów laminarnych. I tak np. dla Re < 10, jest on odwrotnie proporcjonalny do Re, zaś dla większych liczb Re zależność ζ = ζ (Re) można wyrazić w postaci
. Współczynnik n jest mniejszy od jedności, a dla górnych wartości Re przepływu laminarnego może być przyjmowane n = 0,285.

Dla przepływów turbulentnych wpływ liczby Reynoldsa Re na wartości ζ jest nieznaczny. Przy obliczeniach praktycznych przyjmujemy, że nie zależy on od Re a zależy jedynie od rodzaju miejscowej przeszkody - podstawowych parametrów określających ją.

4. Schemat i opis stanowiska

Schemat stanowiska pomiarowego przedstawiono na rysunku 1. Składa się ono z przewodu wzdłuż którego rozmieszczone są miejscowe przeszkody. Przewód jednym końcem połączony jest ze zbiornikiem ciśnieniowym, drugim końcem doprowadzamy ciecz do przelewu mierniczego. Do pomiaru ciśnień zastosowano manometr rtęciowy „U” - 1 oraz cztery układy piezometrów do pomiaru strat energii na załamaniach - I, na kolankach - II, przy gwałtownym zwężeniu przewodu - III oraz przy gwałtownym rozszerzeniu przewodu i zaworze - IV.

Rys. 1. Schemat stanowiska pomiarowego: a - od zbiornika ciśnieniowego, b - do przelewu mierniczego, c - pozioma płaszczyzna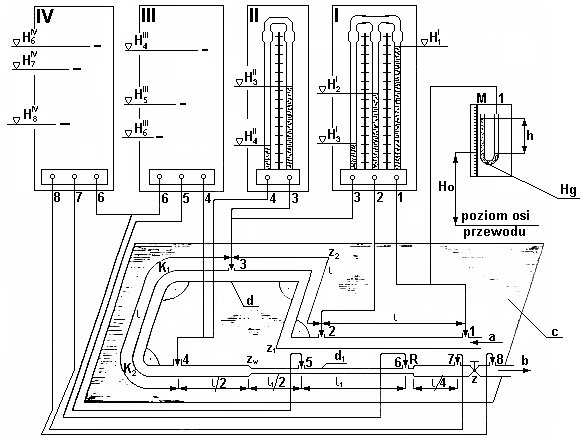

Układy piezometrów III i IV są identyczne jak I. Na rysunku, dla układów III i IV naniesiono tylko wysokości zwierciadeł cieczy w rurkach piezometrycznych - nie przedstawiając samych rurek. Piezometry połączone są w ten sposób, że pozwalają mierzyć straty ciśnienia na określonych odcinkach przewodu bez przeszkód miejscowych i z przeszkodami.

5. Wyniki

T = 30º C ⇒ 303 K

p_ot = 98400 Pa

ρ_p=
=
= 1,13

Wyniki pomiarów:

Pomiar I
Manometr	h1		h2		h3		h4		h5
Wysokość hn	h7	h8	h12	h13	h14	h15	h18	h19	h20	h21
		5	4	54	59	57	62	62	65	65	89
Różnica hn	1		5		5		4		24
hv = |h11-h10|	|62 - 2| = 60
Pomiar II
Manometr	h1		h2		h3		h4		h5
Wysokość hn	h7	h8	h12	h13	h14	h15	h18	h19	h20	h21
		-5	-5	23	25	25	28	28	30	30	45
Różnica hn	10		2		3		2		15
hv = |h11-h10|	|-6 - 29 | = 35

6. Obliczenia

Wielkość Nr pomiaru	Wydatek Q	Prędkość		Liczba Re			Różnica
				v3	v1	Re1	Re2	Re3
		10^-3 m^3/s	m/s		-			m
1		14	9,35				31,4	-9,5
2		10,4	7,13				17,8	-5,95
Wyznaczenie współczynnika ζ
Lokalne straty energii 10^-3[m]				h1	h2	h3	h4	h5
Pomiar 1				1	5	5	4	24
Pomiar 2				0	1	3	2	15
Współczynnik strat lokalnych ζ				ζRoz	ζK	ζK	ζRoz	ζZw
Pomiar 1				0,05	0,25	0,25	0,2	1,22
Pomiar 2				0,08	0,17	0,26	0,17	1,3
ζśr. średnie z pomiaru 1 i 2				0,065	0,21	0,255	0,185	1,26
ζt z literatury
Różnica względna

γ_p= ρ_p · g = 1,13 · 9.81 = 11

γ_m = 8270

obliczenia dla pierwszego pomiaru:

a- prędkości:

b- współczynniki strat lokalnych:

obliczenia dla drugiego pomiaru:

a- prędkości:

b- współczynniki strat lokalnych:

---