Imię i nazwisko: Bartosz Ślęzak	Ćwiczenie nr E8 Sprawdzenie praw Kirhoffa.
Kierunek i rok: Fizyka II rok	Ocena z kolokwium: Data: Podpis:	Ocena ze sprawozdania: Data: Podpis:	Ocena końcowa: Data: Podpis:
Nazwisko prowadzącego zajęcia: dr A. Domagała

1. CZĘŚĆ TEORETYCZNA

Siła elektromotoryczna (SEM) jest liczbowo równa pracy, jaka siły obce wykonują przy przemieszczaniu w przewodniku jednostkowego ładunku dodatniego, praca jest wykonywana kosztem zużywania w źródle energii. Dlatego właśnie wielkość ta nazywana jest siłą elektromotoryczną źródła energii elektrycznej.

Napięciem nazywamy wielkość fizyczną, która jest liczbowo równa pracy, wykonanej przez wypadkowe pola sił kulombowskich i obcych przy przemieszczaniu jednostkowego ładunku dodatniego wzdłuż obwodu.

Siła elektromotoryczna rozkłada się na dwa spadki napięć: U_R=RI na oporze zewnętrznym oraz U_r=rIn a oporze wewnętrznym źródła.

Siłę elektromotoryczną zmierzyć możemy bezpośrednio za pomocą miernika magnetoelektrycznego.

Przepływem prądu stałego rządzą prawa Ohma i Kirchoffa.

Prawo Ohma:

I=f(U)

I [A]

U [V]

Natężenie prądu jest wprost proporcjonalne do napięcia między końcami przewodnika.

U/I=const.

Oporem elektrycznym danego przewodnika nazywamy stosunek napięcia przyłożonego do jego końców do natężenia prądu, który płynie przez przewodnik pod wpływem tego napięcia.

R- opór elektryczny danego przewodnika. /1/

Pierwsze prawo Kirchoffa (prawo węzłów):

Suma algebraicznych natężeń prądów schodzących się w węźle równa jest zeru,

gdzie n jest liczbą schodzących się w węźle przewodników, I_i- natężeniem prądu w węźle. Przyjmujemy, że prądy przychodzące do węzła są dodatnie, a prądy wychodzące z węzła są ujemne.

Drugie prawo Kirchoffa : w każdym obwodzie zamkniętym ,dowolnie wybranym z rozgałęzionej sieci elektrycznej, suma algebraiczna iloczynów natężeń prądu I_i oporów R_i odpowiednich odcinków tego obwodu równa jest sumie algebraicznej SEM w obwodzie:

gdzie n₁ jest liczbą odcinków, na jakie obwód jest podzielony przez węzły. Przy korzystaniu z drugiego prawa Kirchoffa wybieramy określony kierunek obiegu oczka sieci (zgodnie z ruchem wskazówek zegara lub przeciwnie). Prądy których kierunki pokrywają się z kierunkiem obiegu prądu w obwodzie przyjmujemy za dodatnie. Z kolei SEM źródeł prądu uważamy za dodatnie, gdy powodują one przepływ prądu o kierunku zgodnym z kierunkiem obiegu obwodu.

CZĘŚĆ PRAKTYCZNA

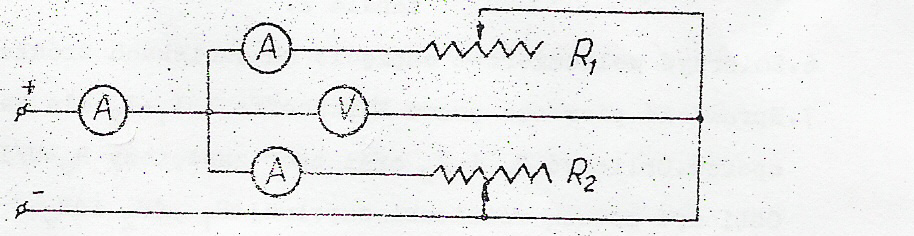
Dla pierwszego obwodu.

Lp.	U[V]	I[A]	I1[A]	I2[A]	I1+I2[A]	R1[Ω]	R2[Ω]	Rw[Ω]
1.	6,8	0,63	0,36	0,29	0,65	18,9	23,4	10,8
2.	6,8	0,42	0,15	0,29	0,44	45,3	23,4	16,2
3.	6,8	0,35	0,08	0,29	0,37	85	23,4	19,4
4.	6,8	0,31	0,04	0,29	0,33	170	23,4	21,9
5.	6,8	0,3	0,03	0,29	0,32	226,7	23,4	22,7
6.	6,8	0,14	0,03	0,13	0,16	226,7	52,3	48,6
7.	6,8	0,08	0,03	0,07	0,1	226,7	97,1	85
8.	6,8	0,06	0,03	0,05	0,08	226,7	136	113,3
9.	6,8	0,05	0,03	0,04	0,07	226,7	170	136
10.	6,8	0,03	0, 03	0,02	0,05	226,7	340	226,6

Dla drugiego obwodu.

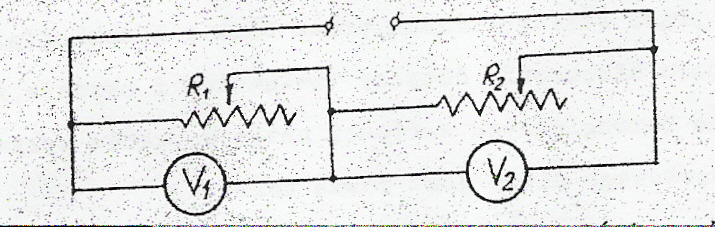
Lp.	U1[V]	U2[V]	U1+U2[V]	ε[V]
1.	3,2	3,6	6,8	6,8
2.	3,9	2,9	6,8	6,8
3.	4,7	2,1	6,8	6,8
4.	5,5	1,3	6,8	6,8
5.	5,9	0,9	6,8	6,8
6.	5,1	1,7	6,8	6,8
7.	4,4	2,4	6,8	6,8
8.	4,0	2,8	6,8	6,8
9.	3,6	3,2	6,8	6,8
10.	3,1	3,7	6,8	6,8

amperomierz: klasa 0,5; zakres 0,75

woltomierz: klasa 0,5; zakres 7,5

Sprawdzam pierwsze prawo Kirchoffa I=I₁+I₂

1. I=I₁+I₂ =0,65A

2. I=I₁+I₂ =0,44A

3. I=I₁+I₂ =0,37A

4. I=I₁+I₂ =0,33A

5. I=I₁+I₂ =0,32A

6. I=I₁+I₂ =0,16A

7. I=I₁+I₂ =0,1A

8. I=I₁+I₂ =0,08A

9. I=I₁+I₂ =0,07A

10.I=I₁+I₂ =0,05A

Obliczam R₁ i R₂ oraz opór zastępczy R_w

1. R₁=18,9 Ω R₂=23,4 Ω R_W=10,8 Ω

2. R₁=45,3 Ω R₂=23,4 Ω R_W=16,2 Ω

3. R₁=85 Ω R₂=23,4 Ω R_W=19,4 Ω

4. R₁=170 Ω R₂=23,4 Ω R_W=21,9 Ω

5. R₁=226,7 Ω R₂=23,4 Ω R_W=22,7 Ω

6. R₁=226,7 Ω R₂=52,3 Ω R_W=48,6 Ω

7. R₁=226,7 Ω R₂=97,1 Ω R_W=85 Ω

8. R₁=226,7 Ω R₂=136 Ω R_W=113,3 Ω

9. R₁=226,7 Ω R₂=170 Ω R_W=136 Ω

10. R₁=226,7 Ω R₂=340 Ω R_W=226,7 Ω

Metodą różniczki zupełnej obliczam niepewności oporów R₁, R₂ i R_W :

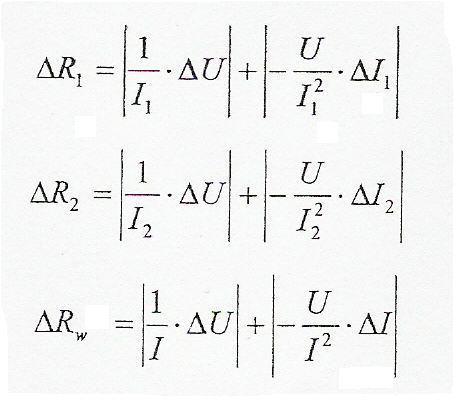
ΔU=0,1[V] ΔI=0,01[A]

Lp.	ΔR1	ΔR2	ΔRw
1.	0,6	1,1	0,33
2.	3,7	1,1	0,63
3.	10,6	1,1	0,85
4.	45	1,1	1,03
5.	78,8	1,1	1,09
6.	78,8	4,8	4,18
7.	78,8	15,3	11,87
8.	78,8	29,2	20,56
9.	78,8	45	29,2
10.	78,8	175	78,89

Sprawdzam czy R_w dla każdego przypadku jest równa

1. R_w=10,56 Ω

2. R_w=15,43 Ω

3. R_w=23,46 Ω

4. R_w=20,57 Ω

5. R_w=21,21 Ω

6. R_w=42,5 Ω

7. R_w=68 Ω

8. R_w=85 Ω

9. R_w=97,15 Ω

10. R_w=136,01 Ω

Sprawdzam drugie prawo Kirchoffa ε=U₁+U₂

1. ε=U₁+U₂=6,8 V

2. ε=U₁+U₂=6,8 V

3. ε=U₁+U₂=6,8 V

4. ε=U₁+U₂=6,8 V

5. ε=U₁+U₂=6,8 V

6. ε=U₁+U₂=6,8 V

7. ε=U₁+U₂=6,8 V

8. ε=U₁+U₂=6,8 V

9. ε=U₁+U₂=6,8 V

10. ε=U₁+U₂=6,8 V

WNIOSKI:

Celem ćwiczenia było sprawdzenie praw Kirchoffa. Z powyższych obliczeń wynika ze spełnione są I i II prawo Kirchoffa, jednak podczas wykonywania ćwiczenia nie uniknąłem błędów które mogły wynikać z niedokładności przyrządów pomiarowych oraz niedoskonałości zmysłów człowieka.

węzłem nazywamy taki punkt rozgałęzionego obwodu, w którym schodzą się więcej niż dwa przewodniki:

---