2.2. Prąd elektryczny w przewodnikach

2.2.1. Prawo Ohma. Rezystancja i przewodność przewodnika

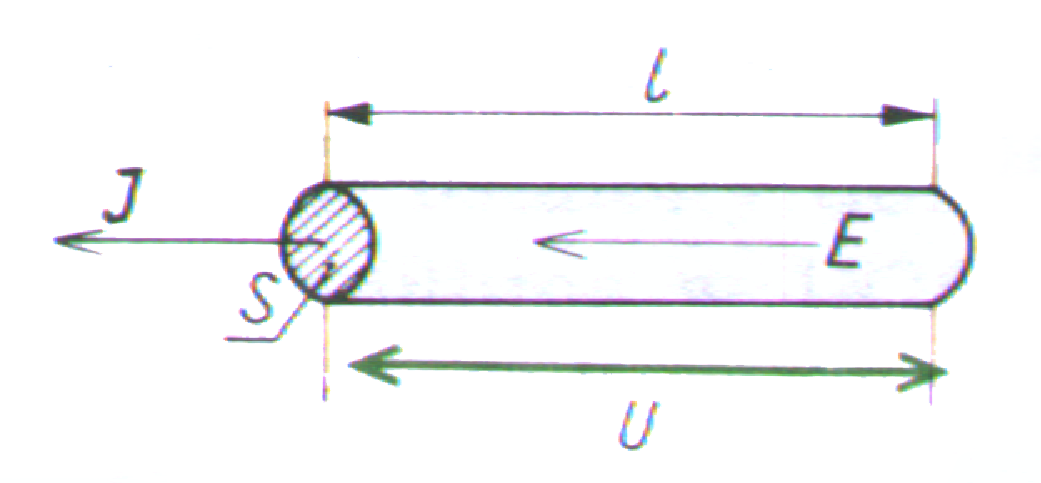
Rozpatrzmy element przewodzący o dłu­gości I i przekroju S wykonany z prze­wodnika pierwszego rodzaju (patrz p. 1.5.), np. metalu (rys. 2.2). Element ten stanowi odcinek przewodu dołączonego do źródła energii elektrycznej, np. do ogniwa.

Rys. 2.2. Element przewodzący

W przewodzie płynie prąd elektryczny 1. Zgodnie ze wzorem (2.3) możemy obli­czyć gęstość tego prądu J. Napięcie na odcinku o długości l oznaczymy przez U. Przepływ prądu w przewodzie wywołuje wewnątrz przewodu pole elektryczne, którego natężenie oznaczymy przez E. Zwrot wektora natężenia pola elektry­cznego E wewnątrz przewodu jest zgod­ny ze zwrotem wektora gęstości prądu J Wektory E' i J są ze sobą ściśle związane. Doświadczalnie stwierdzono bowiem,

że im większa jest wartość natężenia po­la E w przewodzie, tym większa jest gę­stość prądu J, gdyż ruch ładunków w prze­wodzie jest związany z wartością natęże­nia pola elektrycznego działającego na te ładunki. Zatem

J = γ·E (2.4)

przy czym y oznacza współczynnik proporcjonal­ności, zwany konduktywnością materiału, z które­go jest wykonany przewód.

Konduktywność jest zatem wielkością określającą własności przewodzące prze­wodnika. Na podstawie równania (2.4) dla wielkości, napiszemy równanie dla jednostek tych wielkości i stąd określi­my jednostkę konduktywności

[J] A·m S 1

[γ] = = = =

[E] m²·V m Ω·m

m S

W praktyce konduktywność wyrażamy w =10⁶

Ω·mm2 m

Odwrotność konduktywności oznacza­my przez o i nazywamy rezystywnością materiału przewodzącego

1

p = (2.5)

γ

Jednostką rezystywności jest odwrot­ność jednostki konduktywności, czyli 1 omometr

[ρ] = 1Ω·m

Ω·mm2

W praktyce rezystywność wyrażamy w =10^-6 Ω·m

m

Materiały stosowane w elektrotechnice jako przewodniki mają dużą kondukty­wność. Najlepsze zdolności przewodze­nia w temperaturze normalnej wykazują metale czyste. Spośród metali najwięk­szą konduktywność ma srebro. Jednak­

że srebro ze względu na małą wytrzyma­łość mechaniczną i wysoki koszt, jest stosowane tylko do specjalnych celów. Najbardziej rozpowszechnionym mate­riałem przewodzącym jest miedź. Z mie­dzi wykonuje się uzwojenia maszyn ele­ktrycznych, aparatów, przyrządów po­miarowych, przewody linii przesyło­wych, styki itp. Drugim szeroko rozpo­wszechnionym materiałem przewodzą­cym jest aluminium. Stal ma dużo mniej­szą konduktywność od wymienionych materiałów. Wszelkiego rodzaju dodat­ki stopowe zmniejszają konduktywność materiału. W elektrotechnice znajdują też zastosowanie materiały o małej kon­duktywności, czyli dużej rezystywności. Są to tzw. stopy rezystancyjne, wykony­wane jako stopy żelaza, miedzi, manga­nu, niklu, chromu, srebra. Materiały te, w zależności od rodzaju stopu, noszą nazwy: manganin, konstantan, chromo­nikielina, kanthal, megapyr itp. Stopy te stosowane są w przyrządach pomiaro­wych, w urządzeniach grzejnych i in­nych.

W tab. 2.1 zestawiono rezystywności i konduktywności najczęściej stosowa­nych materiałów przewodzących.

W elektrotechnice znajdują zastosowa­nie również materiały o bardzo małej konduktywności (bardzo dużej rezysty­wności) należące do grupy nieprzewo­dników (izolatorów).

Wróćmy raz jeszcze do przedstawione­go na rys. 2.2 elementu przewodnika. Z zależności wiążącej napięcie z natęże­niem pola elektrycznego wynika, że dla elementu z rys. 2.2

U = E·l (2.6)

a na podstawie wzoru (2.3) napiszemy

I=J·S

stąd po uwzględnieniu wzoru (2.4)

I = γ·E·S (2.8)

Stosunek napięcia U określonego zale­żnością (2.6) do prądu 1, określonego zależnością (2.8) nazywamy rezystancji przewodnika i oznaczamy przez R, zatem

U E·l l δ·l

R = = = = (2.9)

I γ·E·S γ·S S

Rezystancja rezystora jest wielkością stałą i wyraża się stosunkiem napięcia na rezystorze do wartości przepływają­cego prądu

U

R=

I

Jednostką rezystancji jest 1 om (1 SZ). Przewodnik ma zatem rezystancję jed­nego oma, jeżeli pod działaniem napię­cia 1 wolta w przewodniku płynie prąd równy 1 amperowi.

Odwrotność rezystancji nazywamy kon­duktancją i oznaczamy przez G, zatem

1

G = (2.10)

R

Jednostką konduktancji jest 1 simens (1 S), będący odwrotnością oma. Ze wzoru (2.9) wynika, że rezystancja prze­wodnika zależy od własności materiału

przewodzącego, którą określa rezystyw­ność lub konduktywność, oraz od dłu­gości przewodnika i jego przekroju. Element przewodzący o rozpatrywa­nych własnościach nazywamy rezysto­rem. Symbol graficzny rezystora przed­stawiono na rys. 2.3.

R I

U

Rys. 2.3. Symbol graficzny rezystora

Związek między napięciem, prądem i re­zystancją został ustalony doświadczal­nie przez G. S. Ohma w 1826 r. i nosi nazwę prawa Ohma.

Napięcie U mierzone na końcach prze­wodnika o rezystancji R podczas prze­pływu prądu I jest równe iloczynowi re­zystaocji i prądu.

Prawo Ohma zapisujemy w dwóch rów­noważnych postaciach

U = RI (2.11)

I = G U (2.12)

Zależność (2.4) ujęta w zapisie wektoro­wym

J = yE (2.13)

nazywana jest prawem Ohma w postaci wektorowej.

---