Szkoła Główna Służby Pożarniczej w Warszawie

Praca zaliczeniowa

Przedmiot:

Podstawy budownictwa

Temat:

Wykonanie projektu obliczeniowego

Wykonał: Konsultował:

mł.asp. Hodorowicz Piotr st. kpt. mgr inż. Ryszard Adamski

mł.asp. Kramarz Rafał

Warszawa 2004r.

Przykład obliczeniowy

Słup wykonany z drewna litego klasy GL 36h o przekroju poprzecznym b x h = 0,26 x 0,40 m i wysokości 4,5m jest usytuowany przy ścianie zewnętrznej pomieszczenia biurowego. Słup jest podparty przegubowo na obu końcach i poddany działaniu osiowych sił ściskających: stałej F_g = 100 kN i zmiennej F_p = 200 kN, jak również ciągłego, równomiernie rozłożonego obciążenia wiatrem w = 1,5 kN/m. Sprawdź stan graniczny słupa w temperaturze pokojowej.

Dane tabelaryczne:

f_m,k = 36

f_c,0,k = 31

k_mod = 0,60

γ_M = 1,3

E_0,mean = 14,7 · 10³ N/mm²

E_0,05 = 11,9 · 10³ N/mm²

G_mean = 0,91· 10³ N/mm²

β_o = 0,65

k_m = 0,8

L = 4,5 m

w = 1,5 m

γ_G = 1,35

γ_Q = 1,5

F_g = 100 kN

F_p = 200 kN

Ψ₀ = 0,7

Ψ₁ = 0,5

Ψ₂ = 0,3

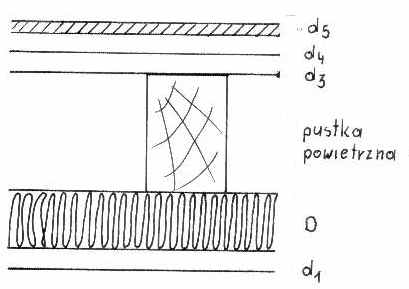
Oznaczenia

• d₁ - płyta nośna

• D - mata izolacyjna z wełny szklanej

• d₂ - sklejka drewniana

• d₄ - płyta twarda z wełny szklanej

• d₅ - sklejka dębowa

Obciążenie technologiczne

• płyta nośna 6 kN/m³

• mata izolacyjna 1,3 kN/m²

• sklejka drewniana 7,5 kN/m³

• płyta twarda z wełny szklanej 2,5kN/m³

• klepka dębowa, deszczułki 0,23kN/m³

Obliczenia

2. A = b · h
   A = 260 · 400
   A = 104000 [mm²]
   

3. W_y = (b · h²)/6
   W_y = (260 · 400²)/6
   W_y = 6933333 [mm³]
   

4. N_d1 = (γ_G · F_g) + (γ_Q,1 · F_p)
   N_d1 = 1,35 · 100 + 1,5 · 200
   N_d1 = 435 [kN]
   

5. q_d1 = γ_Q,2 · Ψ_0,2 · w
   q_{d1 =} 1,5 · 0,7 ·1,5
   q_d1 = 2,1[N/m]
   

6. M_d1 = (q_d1 · L²)/8
   M_d1 = (2,1 · 4,5²)/8
   M_d1 = 5,3 · 10⁶ [N·mm]
   

7. σ_c,0,d1 = N_d1/A
   σ_c,0,d1 = (435 · 10³) /104000
   σ_c,0,d1 = 4,1 [MN/m²]
   

8. σ_m,y,d1 = M_d1/W_y
   σ_m,y,d1 = 5,3 · 10⁶ /6933333
   σ_m,y,d1 = 0,76 [MN/m²]
   

9. N_d2 = (γ_G · F_g) + (Ψ_0,2 · F_p)
   N_d2 = 1,35 · 100 + 1,5 · 200 · 0,5
   N_d2 = 285 [kN]
   

10. q_d2 = γ_Q,1 · w
    q_d2 = 1,5 · 1,5
    q_d2 = 2,25 [kN/m]
    

11. M_d2 = (q_d2 · L²)/8
    M_d2 = (2,25 · 4,5²)/8
    M_d2 = 5,6 [MN/m²]
    

12. σ_c,0,d2 = N_d2/A
    σ_c,0,d2 = 285 · 10³/104000
    σ_c,0,d2 = 2,74 [MN/m²]
    

13. σ_m,y,d2 = M_d2/W_y
    σ_m,y,d2 = 5,6 · 10⁶/6933333
    σ_m,y,d2 = 0,80 [MN/m²]
    

14. f_m,d = (k_mod · f_m,k)/ γ_M
    f_m,d = 0,60 · 36/1,3
    f_m,d = 16,6 [NM/m²]
    

15. f_c,0,d = (k_mod · f_c,0,k)/ γ_M
    f_c,0,d = (0,60 · 31)/1,3
    f_c,0,d = 14,3 [NM/m²]
    

16. i_y = h/12^0,5
    i_y = 400/3,46
    i_y = 115 [mm]
    

17. i_z = b/12^0,5
    i_z = 260/3,46
    i_z = 75 [mm]
    

18. λ_y = L/ i_y
    λ_y = 4500/115
    λ_y = 39
    

19. λ_z = L/ i_z
    λ_z = 4500/75
    λ_z = 60
    

20. σ_c,crit,y = π² · E_0,05/ λ_y²
    σ_c,crit,y = 9,85 · 11900/1521
    σ_c,crit,y = 77 [N/mm²]
    

21. σ_c,crit,z = π² · E_0,05/ λ_z²
    σ_c,crit,z = 9,85 · 11900/3600
    σ_c,crit,z = 32,5 [N/mm²]
    

22. λ_rel,y = (f_c,0,k/σ_c,crit,y)^0,5
    λ_rel,y = (31/77)^0,5
    λ_rel,y = 0,63
    

23. λ_rel,z = (f_c,0,k/σ_c,crit,z)^0,5
    λ_rel,z = (31/39)^0,5
    λ_rel,z = 0,89
    

24. k_y = 0,5[1 + β_o(λ_rel,y - 0,5) + λ_rel,y²]
    k_y = 0,5[1 + 0,65(0,63 - 0,5) + 0,3964]
    k_y = 0,74
    

25. k_z = 0,5[1 + β_o(λ_rel,z - 0,5) + λ_rel,z²]
    k_z = 0,5[1 + 0,65(0,89 - 0,5) + 0,7921
    k_z = 1,02
    




27. k_c,y = [k_y + (k_y² - λ_rel,y²)^0,5] ^-1
    k_c,y = [1,02 + (1,0404 - 0,7921)^0,5] ^-1
    k_c,y = 0,89
    

28. k_c,z = [k_z + (k_z² - λ_rel,z²)^0,5] ^-1
    k_c,z = [0,74(0,5476 - 0,3969)^0,5] ^-1
    k_c,z = 0,55
    

29. σ_m,crit = [π · (b²) · E_0,05 · (G_mean^0,5)]/[L_ef · h · (E_0,mean^0,5)]
    σ_m,crit = [3,14 · (260²⁾ · 11,9 · 10³ · (0,91 · 10³)^0,5]/[4500 · 400 · (14,7 · 10³)^0,5]
    σ_m,crit = 348 [N/mm²]
    

30. λ_rel,m = (f_m,k/ σ_m,crit)^0,5
    λ_rel,m = (36/348)^0,5
    λ_rel,m = 0,32
    

Określenie wartości k_crit

λ_rel,m = 0,32 ≤ 0,75 → k_crit = 1,0

Kombinacja I

[σ_c,0,d1/(k_c,y · f_c,0,d)] + [σ_m,y,d1/( k_crit · f_m,d)
[4,1/(0,89 · 14,3)] + [0,76/(1,0 · 16,6)]
0,32 + 0,045 = 0,35

[σ_m,y,d1/( k_c,z · f_c,0,d)] + [(k_m · σ_m,y,d1)/( k_crit · f_m,d)]
[4,1/(0,55 · 14,3)] + [(0,7 · 0.76)/(1,0 · 16,6)]
0,52 + 0,032 = 0,55

Kombinacja II

[σ_c,0,d2 /(k_c,y · f_c,0,d2)] + [σ_m,y,d2/(k_crit · f_m,d2)]

[2,74 /(0,89 · 14,3)] + [0,80/(1,0 · 16,6)]

0,21 + 0,048 = 0,25

[σ_c,0,d2/(k_c,z · f_c,0,d2)] + [(k_m · σ_m,y,d2)/(k_crit · f_m,d2)]

[2,74/(0,55 · 14,3)] + [(0,7 · 0,80)/( 1,00 · 16,6)]

0,34 + 0,03 = 0,37

Dane tabelaryczne:

fm,k =36 MN/m^2	fc,0,k =31 MN/m^2	E0,mean =14,7·10^3N/m^2	E0,05 =11,9·10^3N/m^2	Gmean=0,91·10^3N/m^2	γM = 1,3
Czas działania obciążenia:		Klasa użytkowania: 3		kmod = 0,60	km = 0,7

β_c = 0,2 (dla drewna litego) β_c = 0,1 (dla drewna klejonego warstwowo)

L.p

Wielkość

Wzór

Wartości liczbowe

Wynik

Jednostka

1

A

b ⋅ h

260 · 400

104000

mm^2

2

W

(b ⋅ h^2) / 6

(260 · 400^2)/6

6933333

mm^3

3

Nd1

γG ⋅Fg + γQ,1 ⋅ Fp

1,35 · 100 + 1,5 · 200

435

kN

4

qd1

γQ,2 ⋅ ψ0,2 ⋅ w

1,5 · 0,7 ·1,5

2,1

N/mm

5

Md1

(qd1 ⋅L^2) / 8

(2,1 · 4,5^2)/8

5,3· 10^6

Nmm

6

σc,0,d1

Nd1/A

(435 · 10^3) /104000

4,1

MN/m^2

7

σm,y,d1

Md1/Wy

5,3 · 10^6 /6933333

0,76

MN/m^2

8

Nd2

γG ⋅Fg + γQ,2 ⋅ ψ0,2 ⋅ Fp

1,35 · 100 + 1,5 · 200 · 0,5

285

kN

9

qd2

γQ,1 ⋅ w

1,5 · 1,5

2,25

kN/m

10

Md2

(qd2 ⋅L^2) / 8

(2,25 · 4,5^2)/8

5,6

MNm^2

11

σc,0,d2

Nd2A

285 · 10^3/104000

2,74

MN/m^2

12

σm,y,d2

Md2/Wy

5,6 · 10^6/6933333

0,80

MN/m^2

13

fm,d

kmod ⋅ fm,k /γM

0,60 · 36/1,3

16,6

MN/m^2

14

fc,0,d

kmod fc,0,k /γM

(0,60 · 31)/1,3

14,3

MN/m^2

15

iy

12^-0,5 ⋅ h

400/3,46

115

mm

16

iz

12^-0,5 ⋅ b

260/3,46

75

mm

17

λy

L / iy

4500/115

39

[-]

18

λz

L / iz

4500/75

60

[-]

19

σc,crit,y

π^2 ⋅ E0,05 /λy^2

9,85 · 11900/1521

77

N/mm^2

20

σc,crit,z

π^2 ⋅ E0,05 /λz^2

9,85 · 11900/3600

32,5

N/mm^2

21

λrel,y

(fc,0,k /σc,crit,y)^0,5

(31/77)^0,5

0,63

[-]

22

λrel,z

(fc,0,k /σc,crit,z)^0,5

(31/39)^0,5

0,89

[-]

23

ky

0,5 [1 + βc (λrel,y - 0,5) + λrel,y^2]

0,5[1 + 0,65(0,63 - 0,5) + 0,3964]

0,74

[-]

24

kz

0,5 [1 + βc (λrel,z - 0,5) + λrel,z^2]

0,5[1 + 0,65(0,89 - 0,5) + 0,7921

1,02

[-]

25

kc,y

[ky + (ky^2 - λrel,y^2)^0,5]^-1

[1,02 + (1,0404 - 0,7921)^0,5] ^-1

0,89

[-]

26

kc,z

[kz + (kz^2 - λrel,z^2)^0,5]^-1

[0,74(0,5476 - 0,3969)^0,5] ^-1

0,55

[-]

27

σm,crit

π⋅b^2⋅E0,05 ⋅Gmean^0,5 Lef ⋅ h ⋅ E0,mean^0,5

[3,14 · (260^2) · 11,9 · 10^3 · (0,91 · 10^3)^0,5]/[4500 · 400 · (14,7 · 10^3)^0,5]

348

N/mm^2

28

λrel,m

(fm,k / σm,crit)^0,5

(36/348)^0,5

0,32

[-]

Określenie wartości kcrit

Dla λrel,m:

kcrit wynosi:

≤ 0,75

1,0

0,75 < λrel,m ≤1,4

1,56 - 0,75 λrel,m

1,56 - 0,75 · 0,32

1,32

[-]

> 1,4

(λrel,m)^-2

1/(0,32^2)

9,7

[-]

Sprawdzenie stanów granicznych nośności:

Kombi-nacja 1

σc,0,d1 /(kc,y⋅fc,0,d1)+σm,y,d1/(kcrit⋅fm,d1)

[4,1/(0,89 · 14,3)] + [0,76/(1,0 · 16,6)]

0,35

≤ 1,0

σc,0,d1 /(kc,z⋅fc,0,d1)+(km⋅σm,y,d1)/(kcrit⋅fm,d1)

[4,1/(0,55 · 14,3)] + [(0,7 · 0.76)/(1,0 · 16,6)]

0,55

Kombi-nacja 2

σc,0,d2 /(kc,y⋅fc,0,d2)+σm,y,d2/(kcrit⋅fm,d2)

[2,74 /(0,89 · 14,3)] + [0,80/(1,0 · 16,6)]

0,25

≤ 1,0

σc,0,d2/(kc,z⋅fc,0,d2)+(km⋅σm,y,d2)/(kcrit⋅fm,d2)

[2,74/(0,55 · 14,3)] + [(0,7 · 0,80)/( 1,00 · 16,6)]

0,37

Przykład obliczeniowy

Zaprojektować belkę podstropową z drewna klejonego warstwowo klasy 3 o długości 4,5 m i przekroju poprzecznym b x h = 0,26 x 0,40 m, swobodnie podpartą na dwóch słupach drewnianych. Belki o rozstawie a = 1,5 m podpierają strop lekki w pomieszczeniu biurowym. Sprawdzić stany graniczne nośności i użytkowalności belki dla następujących danych:

Dane tabelaryczne:

f_m,k = 36

E_0,mean =14,7·10³N/m²

E_0,05 =11,9·10³N/m²

G_mean=0,91·10³N/m²

q_p = 5,33 [kN/m²]

γ_M = 1,3

p_w = 420 · 10^-2

1. Q_k1 = p_k1 · h_p,1 · 10^-2
   Q_k1 = 6 · 0,025
   Q_k1 = 0,15
   

2. Q_k2 = p_insD · h_insD · 10^-2
   Q_k2 = 1,3 · 0,065
   Q_k2 = 0,084 [kN/m²]
   

3. Q_k3 = p_k3 · h_p,3 · 10^-2
   Q_k3 = 7,5 · 0,02
   Q_k3 = 0,15 [kN/m²]
   

4. Q_k4 = p_k4 · h_p,4 · 10^-2
   Q_k4 = 2,5 · 0,03
   Q_k4 = 0,075 [kN/m²]
   

5. Q_k5 = p_k5 · h_p,5 · 10^-2
   Q_k5 = 0,23 · 0,003
   Q_k5 = 0,006 [kN/m²]
   

6. Q_k = Q_k1 + Q_k2 + Q_k3 + Q_k4 + Q_k5
   Q_k = 0,15 + 0,084 + 0,15 + 0,075 + 0,006
   Q_k = 0,44 [kN/m²]
   

7. A = b · h
   A = 0,26 · 0,40
   A = 0,104 [m²]
   

8. W = (b · h²)/6
   W = (0,26 · 0,40²)/6
   W = 0,006
   

9. J = (b · h³)/12
   J = (0,26 · 0,40³)/12
   J = 0,13 [m⁴]

10. q_g = a · Q_k + A · p_w · 10^-2
    q_g = 1,50 · 0,46 + 0,104 · 420 · 10^-2
    q_g = 5,058 [kN/m]
    

11. q_d = q_g · γ_G + a · q_p · γ_Q
    q_d = 5,058 · 1,35 + 1,50 · 5,33 · 1,5
    q_d = 10,82 [kN/m]
    

12. M_d,max = (q_d · L²)/8
    M_d,max = (10,82 · 19,36)/8
    M_d,max = 26,19 [MNm]
    

13. σ_m,d = M_d,max/W
    σ_m,d = 26,19/0,006
    σ_m,d = 1366,3 [MNm²]
    

14. f_m,d = (k_mod · f_m,k)/ γ_M
    f_m,d = (18,46 · 40)/1,3
    f_m,d = 568 [MNm²]
    

15. E_d,05 = (k_mod · E_0,05)/ γ_M
    E_d,05 = (0,60 · 9,4)/1,3
    E_d,05 = 4,33 [GNm²]
    

16. σ_m,crit = [π·b²·E_0,05· _mean^0,5]/[L_ef ·h·E₀,_mean]
    σ_m,crit = [3,14·0,26²·9400·880^0,5]/[4,4·0,40·14000^0,5]
    σ_m,crit = 283 [MNm²]
    

17. λ_rel,m = (f_m,k/ σ_m,crit)^0,5
    λ_rel,m = (40/283)^0,5
    λ_rel,m = 0,37
    

Określenie wartości k_crit

λ_rel,m = 0,32 ≤ 0,75 → k_crit = 1,0

1,56 - 0,75 λ_rel,m

1,56 - 0,75 · 0,37 = 0,29

(λ_rel,m)^-2

(0,37)^-2 = 7,35

Sprawdzenie warunków nośności:

σ_m,d/(kcrit · fm,d) ≤ 1

1366,3/(1 · 568) ≤ 1

2,40 ≤ 1

Sprawdzenie stanów granicznych używalności:

U_net,fin = L/250

U_net,fin = 4,4/250

U_net,fin = 0,0176 [m]

U_net,fin = L/300

U_net,fin = 4,4/300
U_net,fin = 0,014 [m]

U_{M dla l/h ≤ 20} = [5 · q · L⁴]/[384 · E_o,mean^0,5 · J]
U_{M dla l/h ≤ 20} = [5 · 5,33 · 4,4⁴]/[384 · 14 · 0,13]
U_{M dla l/h ≤ 20} = 14,29 [m]

U_M + U_{v dla L/h > 20} = U_M · [1 + 19,2 · (h/L)²]

U_M + U_{v dla L/h > 20} = [1 + 19,2 · (0,40/4,4)²]
U_M + U_{v dla L/h > 20} = 1,15 [m]

Dane tabelaryczne:

fm,k =36 MN/m^2

E0,mean =14,7·10^3N/m^2

E0,05 =11,9·10^3N/m^2

Gmean=0,91·10^3N/m^2

^q^p^=^5,33^kN/m^2

γM = 1,3

Sprawdzenie stanów granicznych nośności:

Lp	Wielkość	Wzór		Wartości liczbowe	Wynik	Jednostka
1	Qk,1	ρk1 ⋅ hp,1		6 · 0,025	0,15	kN/m^2
2	Qk,2	ρinsD ⋅ hins,D		1,3 · 0,065	0,084	kN/m^2
3	Qk,3	ρk3 ⋅ hp,3 ⋅		7,5 · 0,02	0,15	kN/m^2
4	Qk,4	ρk4 ⋅ hins,4 ⋅		2,5 · 0,03	0,075	kN/m^2
5	Qk,5	ρk5 ⋅ hp,5 ⋅		0,23 · 0,003	0,006	kN/m^2
6	Qk	Qk,1+Qk,2+Qk,3+Qk,4+Qk,5		0,15 + 0,084 + 0,15 + 0,075 + 0,006	0,44	kN/m^2
7	A	b ⋅ h		0,26 · 0,40	0,104	m^2
8	W	(b ⋅ h^2) / 6		(0,26 · 0,40^2)/6	0,006	m^3
9	I	(b h^3) /12		(0,26 · 0,40^3)/12	0,13	m^4
10	qg	a ⋅ Qk + A ⋅ ρw ⋅ 10^-2		1,50 · 0,46 + 0,104 · 420 · 10^-2	5,058	kN/m
11	qd	qg ⋅ γG + a ⋅ qp ⋅ γQ		5,058 · 1,35 + 1,50 · 5,33 · 1,5	10,82	kN/m
12	Md,max	(qd ⋅L^2) / 8		(10,82 · 19,36)/8	26,19	MNm
13	σm,d	Md,max/W		26,19/0,006	1366,3	MN/m^2
14	fm,d	kmod ⋅ fm,k /γM		(18,46 · 40)/1,3	568	MN/m^2
15	Ed,05	kmod ⋅ E0,05 /γM		(0,60 · 9,4)/1,3	4,33	GN/m^2
16	σm,crit	π ⋅ b^2⋅ E0,05 ⋅ Gmean^0,5 Lef ⋅ h ⋅ E0,mean^0,5		[3,14·0,26^2·9400·880^0,5]/[4,4·0,40·14000^0,5]	283	MN/m^2
17	λrel,m	(fm,k / σm,crit)^0,5		(40/283)^0,5	0,37	[-]
Określenie wartości kcrit
Dla λrel,m:			kcrit wynosi:
0,75			1,0			[-]
0,75 < λrel,m ≤1,4			1,56 - 0,75 λrel,m	1,56 - 0,75 · 0,37	0,29	[-]
> 1,4			(λrel,m)^-2	(0,37)^-2	7,35	[-]
Sprawdzenie warunku nośności:
σm,d /(kcrit⋅fm,d) ≤ 1				1366,3/(1 · 568) ≤ 1	2,40

Sprawdzenie stanów granicznych używalności:

Lp	Wielkość	Wzór	Wartości liczbowe	Wynik	Jednostka
1	unet,fin nieotynkowana	L/250	4,4/250	0,0176	m
2	unet,fin otynkowana	L/300	4,4/300	0,014	m
3	uM dla L/h ≤ 20	5 ⋅ q ⋅ L^4­­­___ 384 ⋅ E0,mean ⋅ I	[5 · 5,33 · 4,4^4]/[384 · 14 · 0,13]	14,29	m
4	uM + uv dla L/h > 20	uM [1+19,2 (h/L)^2]	[1 + 19,2 · (0,40/4,4)^2]	1,15	m

---