4. Miary zróżnicowania.

Ważnym problemem jest pomiar i liczbowe określenie wielkości zróżnicowania wartości badanej cechy. Miary dotyczące tego zagadnienia nazywamy miarami zróżnicowania (zmienności, rozproszenia, dyspersji).

Do najczęściej używanych miar zróżnicowania należą:

• rozstęp,

• odchylenie standardowe,

• wariancja,

• odchylenie ćwiartkowe,

• rozstęp kwartylny,

• przedział zmienności (klasyczny i pozycyjny),

• współczynnik zmienności (klasyczny i pozycyjny).

4.1 Rozstęp.

Najprostszą miarą zróżnicowania jest rozstęp, czyli empiryczny obszar zmienności. Miarę tę dla cechy
definiuje się wzorem

,

gdzie
i
są odpowiednio największą i najmniejszą wartością cechy.

W rozważanym przez nas przykładzie dla cech
- staż pracy w latach i
- dzienna wydajność w sztukach, miarę tę można obliczyć odczytując z danych indywidualnych (rozkładu empirycznego) najmniejszą i największą wartość cechy.

Korzystając z modułu Statystyki opisowe w pakiecie STATISTICA 6.0 otrzymujemy wydruk:

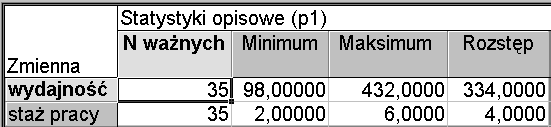
Miara ta, mimo oczywistych zalet (prostota obliczeń, jasny sens logiczny), jest używana tylko przy wstępnej analizie, gdyż opierając się na dwóch skrajnych wartościach, nie mierzy rzeczywistego rozproszenia między jednostkami (elementami) zbiorowości. Wielkość rozstępu będzie wysoka wtedy, gdy rozproszenie jest duże, ale również wtedy, gdy wartość jednej, przypadkowej jednostki odbiega od pozostałych, mało zróżnicowanych między sobą. Dobra miara zróżnicowania musi zatem uwzględniać cały rozkład badanej cechy.

4.2 Odchylenie standardowe.

Największe zastosowanie do badania zróżnicowania wartości badanej cechy ma klasyczna miara zmienności zwana odchyleniem standardowym, oznaczana literą
.

Odchylenie standardowe wyznaczamy według wzorów:

• dane indywidualne cechy skokowej:
  

,

• dane indywidualne cechy ciągłej:
  

.

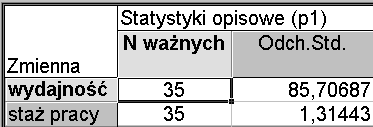
Obliczanie odchylenia standardowego według tych wzorów jest uciążliwe, szczególnie w przypadku prób o dużych liczebnościach. Korzystając z modułu Statystyki opisowe w pakiecie STATISTICA 6.0 otrzymujemy wydruk:

• szereg rozdzielczy cechy skokowej:
  

.

Aby obliczyć odchylenie standardowe według tego wzoru zbudujemy tabelę roboczą

2	9	-1,49	2,2201	19,9809
3	12	-0,49	0,2401	2,8812
4	6	0,51	0,2601	1,5606
5	4	1,51	2,2801	9,1204
6	4	2,51	6,3001	25,2004
	35	xxx	xxx	58,7435

Skąd

.

Otrzymany wynik można skomentować, że staż pracy poszczególnych pracowników różnił się od średniego stażu pracy, wynoszącego
, przeciętnie o
.

• szereg rozdzielczy cechy ciągłej:
  

.

Aby obliczyć odchylenie standardowe według tego wzoru zbudujemy tabelę roboczą

90 - 160	125	11	-88	7744	85184
160 - 230	195	13	-18	324	4212
230 - 300	265	4	52	2704	10816
300 - 370	335	5	122	14884	74420
370 - 440	405	2	192	36864	73728
	xxx	35	xxx	xxx	248360

.

Oznacza to, że dzienna wydajność poszczególnych pracowników różniła się od średniej dziennej wydajności, wynoszącej
sztuk, przeciętnie o
sztuki.

4.3 Wariancja.

Klasyczną miarą zmienności (zróżnicowania, dyspersji) jest również wariancja, oznaczana literą
. Wariancję wyznaczamy według wzoru:

niezależnie od tego, czy cecha jest zadana w postaci danych indywidualnych (rozkładu empirycznego), czy też w postaci szeregu rozdzielczego.

Wariancja jest przede wszystkim używana do celów wnioskowania statystycznego.

4.4 Odchylenie ćwiartkowe.

Pozycyjną miarą zmienności jest również odchylenie ćwiartkowe, oznaczane literą
. Odchylenie ćwiartkowe wyznaczamy według wzoru:

niezależnie od tego, czy cecha jest zadana w postaci danych indywidualnych (rozkładu empirycznego), czy też w postaci szeregu rozdzielczego.

Ponieważ kwartyl pierwszy oddziela czwartą część jednostek o najniższych wartościach, a kwartyl trzeci - czwartą część jednostek o najwyższych wartościach, więc odchylenie ćwiartkowe mierzy rozpiętość cechy połowy najbardziej typowych jednostek zbiorowości.

Odliczymy odchylenie ćwiartkowe w naszym przykładzie.

• dane indywidualne cechy skokowej:
  

.

Otrzymany wynik można skomentować, że staż pracy najbardziej typowych pracowników różnił się od środkowego stażu pracy, wynoszącego
, przeciętnie o
.

• szereg rozdzielczy cechy skokowej:
  

.

• dane indywidualne cechy ciągłej:
  

.

Oznacza to, że dzienna wydajność najbardziej typowych pracowników różniła się od środkowej dziennej wydajności, wynoszącej
sztuk, przeciętnie o
sztuki.

• szereg rozdzielczy cechy ciągłej:
  

.

4.5 Rozstęp kwartylny.

Pozycyjną miarą zmienności (zróżnicowania, dyspersji) jest również rozstęp kwartylny, oznaczany literą
. Rozstęp kwartylny wyznaczamy według wzoru:

,

stąd bezpośrednio wynika, że
.

Korzystając z modułu Statystyki opisowe w pakiecie STATISTICA 6.0 otrzymujemy wydruk:

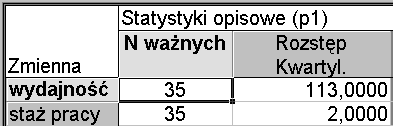
4.6 Przedział zmienności.

Korzystając z miar klasycznych (średniej i odchylenia standardowego) można zbudować klasyczny przedział zmienności postaci:

,

który z reguły zawiera od 50% do 80% wartości badanej cechy. Jeżeli mamy 50 ÷ 60% wartości w tym przedziale, to mówimy o silnym (dużym) zróżnicowaniu wartości cechy. Jeżeli do tego przedziału należy 70 ÷ 80% wartości, to mówimy o słabym (małym) zróżnicowaniu. Jeżeli otrzymamy wynik 60 ÷ 70%, to można mówić o zróżnicowaniu średnim (przeciętnym).

Na podstawie otrzymanych wyników dla cechy
- staż pracy:
,
, mamy

.

Analizując dane indywidualne lub szereg rozdzielczy tej cechy, możemy stwierdzić, że do tego przedziału należy 18 wartości, co stanowi 51% wartości, a zatem mamy w tym przypadku silne zróżnicowanie (dużą zmienność) wartości badanej cechy.

Z wydruków komputerowych można odczytać, że
,
, a więc przedział zmienności dla cechy
jest postaci:

,

nie różni się zatem zasadniczo od zbudowanego na podstawie parametrów obliczonych z szeregu rozdzielczego badanej cechy.

Dla cechy
- dzienna wydajność otrzymaliśmy następujące wartości parametrów:
,
, stąd

.

Analizując szereg rozdzielczy tej cechy, nie można stwierdzić ile wartości należy do tego przedziału. Z danych indywidualnych wynika, że do tego przedziału należy 24 wartości, co stanowi 69% wartości, a zatem mamy w tym przypadku średnie (przeciętne) zróżnicowanie wartości badanej cechy, chociaż można nawet powiedzieć, że zróżnicowanie jest dość słabe (dość mała zmienność).

Z wydruków komputerowych można odczytać, że
,
, a więc przedział zmienności dla cechy
jest postaci:

,

nie różni się zatem zasadniczo od zbudowanego na podstawie parametrów obliczonych z szeregu rozdzielczego badanej cechy.

Wnioski dotyczące zróżnicowania badanych cech wyciągnięte na podstawie zbudowanych klasycznych przedziałów zmienności należy uważać za wstępne. Lepszym kryterium badania zróżnicowania będzie podany dalej klasyczny współczynnik zmienności.

Korzystając z miar pozycyjnych (mediany i odchylenia ćwiartkowego) można zbudować pozycyjny przedział zmienności postaci:

,

który z reguły zawiera od 30% do 60% wartości badanej cechy. Jeżeli mamy 30 ÷ 40% wartości w tym przedziale, to mówimy o silnym (dużym) zróżnicowaniu wartości cechy. Jeżeli do tego przedziału należy 50 ÷ 60% wartości, to mówimy o słabym (małym) zróżnicowaniu. Jeżeli otrzymamy wynik 40 ÷ 50%, to można mówić o zróżnicowaniu średnim (przeciętnym).

Dla cechy skokowej
- stażu pracy, z ustawionych w ciągu niemalejącym danych indywidualnych otrzymaliśmy
,
,
oraz
, a więc

.

Analizując dane indywidualne tej cechy, możemy stwierdzić, że do tego przedziału należy 12 wartości, co stanowi 34% wartości, a zatem mamy w tym przypadku silne zróżnicowanie (dużą zmienność) wartości badanej cechy.

Analizując szereg rozdzielczy, otrzymaliśmy kolejno:
,
,
oraz
, a więc

.

Analogiczne wartości tych parametrów można odczytać z wydruku komputerowego, a więc otrzymamy taki sam pozycyjny przedział zmienności.

Analizując dane indywidualne tej cechy, możemy stwierdzić, że do tego przedziału należy 27 wartości, co stanowi 77% wartości, a zatem mamy w tym przypadku słabe, a nawet bardzo słabe zróżnicowanie (małą zmienność) wartości badanej cechy.

Która z ocen zróżnicowania jest bliższa prawdy przekonamy się później, analizując pozycyjny współczynnik zmienności.

Dla cechy ciągłej
- dziennej wydajności, z ustawionych w ciągu niemalejącym danych indywidualnych otrzymaliśmy
,
,
oraz
, a więc

.

Analizując dane indywidualne tej cechy, możemy stwierdzić, że do tego przedziału należy 21 wartości, co stanowi 60% wartości, a zatem mamy w tym przypadku słabe, a nawet bardzo słabe zróżnicowanie wartości badanej cechy.

Analizując szereg rozdzielczy, otrzymaliśmy kolejno:
,
,
oraz
, a więc

.

Analizując dane indywidualne tej cechy, możemy stwierdzić, że do tego przedziału należy 23 wartości, co stanowi 66% wartości, a więc potwierdza bardzo słabe zróżnicowanie wartości badanej cechy.

Z wydruków komputerowych mamy:
,
,
oraz
, a więc

.

Do tego przedziału należy 23 wartości, co stanowi 66% wartości, a więc to jeszcze raz potwierdza bardzo słabe zróżnicowanie wartości badanej cechy.

Wnioski dotyczące zróżnicowania badanych cech wyciągnięte na podstawie zbudowanych pozycyjnych przedziałów zmienności należy uważać za wstępne. Lepszym kryterium badania zróżnicowania będzie podany dalej pozycyjny współczynnik zmienności.

Warto jeszcze zauważyć, że klasyczny przedział zmienności jest podstawą do oceny stopnia rozproszenia (zróżnicowania, zmienności) wszystkich wartości cechy względem średniej wartości cechy, natomiast pozycyjny przedział zmienności mierzy stopień rozproszenia tylko połowy wartości cechy (zawartych między kwartylami) względem mediany.

4.7 Współczynnik zmienności.

Korzystając z miar klasycznych (średniej i odchylenia standardowego) można obliczyć klasyczny współczynnik zmienności, który wyraża się wzorem

,

przy czym zachodzi nierówność
. Mnożąc powyższy ułamek przez 100 można klasyczny współczynnik zmienności podać w ujęciu procentowym. Wtedy oczywiście
. Jeżeli
, to mówimy o bardzo słabym zróżnicowaniu (bardzo małej zmienności) wartości cechy. Jeżeli
, to mówimy o słabym zróżnicowaniu (małej zmienności) wartości cechy. Jeżeli
, to mówimy o zróżnicowaniu średnim, przeciętnym (średniej, przeciętnej zmienności) wartości cechy. Jeżeli
, to mówimy o silnym zróżnicowaniu (dużej zmienności) wartości cechy. Jeżeli
, to mówimy o bardzo silnym zróżnicowaniu (bardzo dużej zmienności) wartości cechy.

W naszym przykładzie dla cechy
- stażu pracy, korzystając z wartości parametrów obliczonych z szeregu rozdzielczego, mamy

,

co świadczy o słabym zróżnicowaniu (małej zmienności, słabym rozproszeniu, silnym skupieniu) wartości badanej cechy.

Na podstawie wydruków komputerowych mamy

,

co potwierdza poprzednią ocenę stopnia zróżnicowania wartości cechy.

Dla cechy
- dzienna wydajność, korzystając z wartości parametrów obliczonych z szeregu rozdzielczego, mamy

,

co świadczy o słabym zróżnicowaniu (małej zmienności, słabym rozproszeniu, silnym skupieniu) wartości badanej cechy.

Na podstawie wydruków komputerowych mamy

,

co praktycznie potwierdza poprzednią ocenę stopnia zróżnicowania wartości cechy.

Korzystając z miar pozycyjnych (mediany i odchylenia ćwiartkowego) można obliczyć pozycyjny współczynnik zmienności według wzoru:

,

przy czym zachodzi nierówność
. Mnożąc powyższy ułamek przez 100 można klasyczny współczynnik zmienności podać w ujęciu procentowym. Wtedy oczywiście
. Jeżeli
, to mówimy o bardzo słabym zróżnicowaniu (bardzo małej zmienności) wartości cechy. Jeżeli
, to mówimy o słabym zróżnicowaniu (małej zmienności) wartości cechy. Jeżeli
, to mówimy o zróżnicowaniu średnim, przeciętnym (średniej, przeciętnej zmienności) wartości cechy. Jeżeli
, to mówimy o silnym zróżnicowaniu (dużej zmienności) wartości cechy. Jeżeli
, to mówimy o bardzo silnym zróżnicowaniu (bardzo dużej zmienności) wartości cechy.

W naszym przykładzie mamy kolejno:

• dane indywidualne cechy skokowej:
  

,

• szereg rozdzielczy cechy skokowej:
  

,

• wydruki komputerowe

,

a więc we wszystkich przypadkach stwierdzamy słabe zróżnicowanie (małą zmienność, słabe rozproszenie, silne skupienie) wartości badanej cechy.

Analogicznie

• dane indywidualne cechy skokowej:
  

,

• szereg rozdzielczy cechy skokowej:
  

,

• wydruki komputerowe

,

a więc we wszystkich przypadkach stwierdzamy słabe zróżnicowanie (małą zmienność, słabe rozproszenie, silne skupienie) wartości badanej cechy.

Warto jeszcze zaznaczyć, że klasyczny współczynnik zmienności jest podstawą do oceny stopnia rozproszenia (zróżnicowania, zmienności) wszystkich wartości cechy względem średniej wartości cechy, natomiast pozycyjny współczynnik zmienności mierzy stopień rozproszenia tylko połowy wartości cechy (zawartych między kwartylami) względem mediany.

---