LABORATORIUM FIZYKI II					Ćwiczeni nr: 1
Wydział: WIM		Grupa: 2.3		Zespół: 7	Data: 30.11.1999
Nazwisko i imię: Radosław Skwira					Przygotowanie:
Temat ćwiczenia: Charakterystyka robocza i czas martwy licznika Geigera - Mullera					Zaliczenie:
Sprawozdanie przyjęto:	Podpis:		Prowadzący:		Data:

Cel ćwiczenia:

Ćwiczenie miało na celu:

- zapoznanie z działaniem i zastosowaniem licznika Geigera - Mullera,

- wyznaczenie charakterystyki licznika Geigera - Mullera,

- wyznaczenie jego czasu martwego.

Część teoretyczna:

Zastosowany przez nas licznik Geigera-Mullera jest detektorem używanym do wykrywania promieniowania wysyłanego przez izotopy radioaktywne. Zbudowany jest on z dwóch elektrod:

• cylindrycznej katody,

• umie­szczonej wzdłuż osi katody odizolowanej nici - anody.

Całość jest szczelnie zamknięta i wypełniona gazem pod zmniejszonym ciśnieniem.

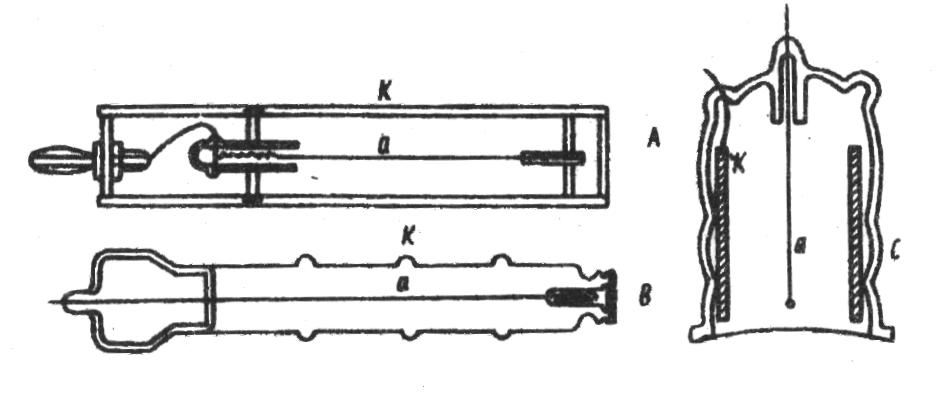
Do elektrod doprowadza się wysokie napięcie, przy czym nić - anoda otrzymuje potencjał dodatni. Poniższy rysunek (rys.1) przedstawia budowę licznika G - M na promieniowanie β kielichowego lub sztorcowego (rys.1c) oraz licznika na promie­niowanie γ cylindrycznego (rys. 1a, 1b).

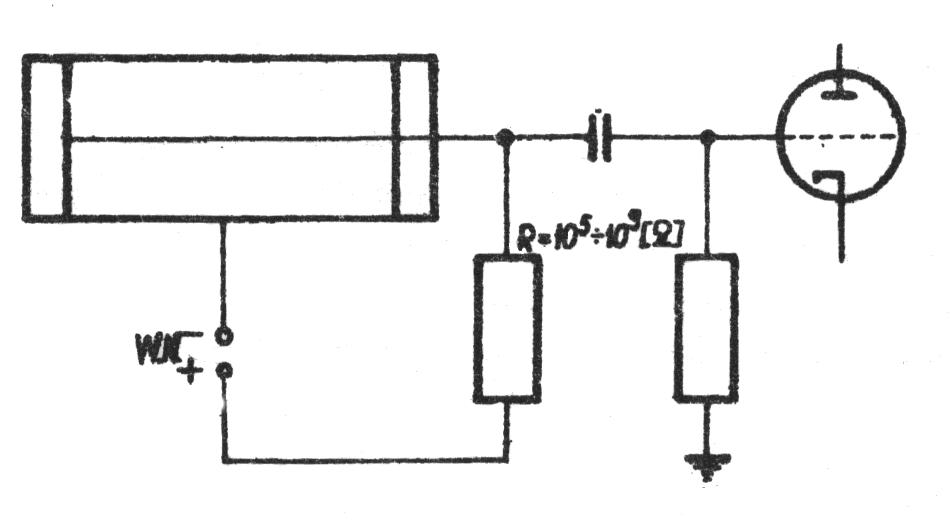
Rysunek 2 pokazuje spo­sób włączenia licznika do aparatury pomiarowej.

Liczniki okien­kowe na promieniowanie γ zbudo­wane są podobnie jak liczniki na promieniowanie β nie po­siadają jednak okienka mikowego względnie okienko to ma wię­kszą grubość. Mimo to liczniki na promieniowanie beta rejestrują promieniowanie gamma, jednak nie stosuje się ich do jego wykrywania ze względu na małą wydajność. Wynika to z faktu, że działanie licznika na promieniowanie gamma spowodowane jest powstawaniem wtórnych elektronów ( promieniowanie gamma nie jonizuje bezpośrednio ośrodka, przez które przechodzi w przeciwieństwie do beta). Należy zatem grubość ścianki dobrać tak, aby powstawało ich możliwie dużo.

Działanie licznika G - M. jest następujące:

Gdy przez komorę licznika przejdzie cząstka naładowana lub kwant gamma, gaz zawarty w liczniku zostaje zjonizowany ( bezpośrednio lub przez elektrony wtórne). Tak powstałe elektrony i jony poruszają się pod wpływem przyłożonego pola elektrycznego ku katodzie i anodzie. Gdy zostaną przyśpieszone (przez pole) do odpowiednio

dużych energii to mogą wzbudzać lub jonizować dalsze atomy gazu. Procesom tym towarzyszy emisja promieniowania ultrafioletowego, które poprzez proces fotojonizacji przyśpieszają proces rozprzestrzeniania się wyładowania elektrycznego na całą komorę. Na oporze R załączonym szeregowo do obwodu zasilania licznika powstaje impuls napięcia, który jest sygnałem na wyjściu. Aby licznik mógł zarejestrować przejście kolejnej cząstki lub też kwantu gamma wyładowanie lawinowe musi zostać zatrzymane w jak najkrótszym czasie. Osiąga się to, poprzez zastosowanie odpowiedniej aparatury elektronicznej lub przez wypełnienie komory licznika odpowiednią mieszaniną gazów (np. argon z dodatkiem ok. 10% par alkoholu).

Licznik G - M. nie daje możliwości rozróżnienia poszczególnych cząstek, uwarunkowane jest to, zakresem napięć, w którym licznik pracuje. W tym obszarze wszystkie impulsy mają tą samą wartość niezależnie od zdolności jonizacyjnej cząstek.

Przebieg ćwiczenia:

1. Próg pracy licznika (taką wartość napięcia poniżej której impulsy są tak małe, że urządzenie liczące ich nie rejestruje).

Nr Pomiaru	VP [V]
1	520

Tabela 1 Zmierzona wartość progowa.

2. Zdejmowanie charakterystyki roboczej badanego licznika. W tym celu napięcie ustawiliśmy na 720V a czas liczenia na 1 min., po dokonaniu pomiaru liczby zliczeń w zadanym czasie zmniejszaliśmy napięcie o 10V i powtarzaliśmy pomiar, aż do osiągnięcia napięcia progowego.

Wyniki przedstawia tabela 2.

U [V]	N [Imp]	I [Imp/min]
720	19337	19337	17,952
710	18056	18056	17,347
700	16296	16296	16,480
690	15189	15189	15,910
680	14250	14250	15,411
670	13801	13801	15,166
660	13089	13089	14,769
650	12821	12821	14,617
640	12529	12529	14,450
630	12307	12307	14,321
620	12105	12105	14,203
610	12235	12235	14,279
600	11685	11685	13,955
590	11723	11723	13,977
580	11667	11667	13,944
570	11438	11438	13,807
560	11154	11154	13,634
550	11317	11317	13,733
540	10883	10883	13,467
530	9821	9821	12,793
520	1	1	0,129

Na podstawie danych zawartych w powyższej tabeli wykreśliliśmy charakterystykę licznika (wykres nr 1).

Dysponując wykresem przystąpiłem do wyznaczenia:

1. napięcia pracy licznika:

stąd :

U Pracy = 608,5 [V]

2. długości plateau:

V₂ - V₁ = 685 -532 = 153 [V]

3. nachylenia plateau:

Nachylenie = 0,256

Na podstawie zebranych dotąd danych sporządziłem metryczkę licznika (tab. 3)

Napięcie progowe [V]	≈ 520
Napięcie pracy [V]	608,5
Długość plateau [V]	153
Nachylenie plateau	0,256

Tabela 3 Metryczka licznika.

Kolejny etap ćwiczenia polegał na wyznaczeniu czasu martwego licznika G - M. W tym celu pod licznikiem umieściliśmy preparat i dokonaliśmy pomiaru w ciągu 240 sekund. Następnie nie ruszając pierwszego preparatu umieściliśmy pod licznikiem drugi i ponownie zmierzyliśmy szybkość liczenia w ciągu 240 sekund. Potem usunęliśmy z komory licznika preparat pierwszy i przeprowadziliśmy pomiary aktywności preparatu drugiego. Na końcu z komory usunęliśmy wszystkie próbki i rozpoczęliśmy pomiar liczby zliczeń także w czasie 240 sekund (zdjęliśmy tzw. „tło licznika”). Otrzymane wartości zawiera tabela 4.

Nr Preparatu	t [min]	N [imp]	IN [imp/min]	I = IN - Itła
1	240	28352	7088	7077
1+2	240	63725	15931,25	15920,25
2	240	38981	9745,25	9734,25
0	240	44	11	-

Korzystając ze wzoru oraz uwzględniając tło:

wyliczyłem czas martwy licznika:

τ = 6,466 ∙ 10^-6 [min]

τ = 3,879 ∙ 10-4 [s]

błąd czasu martwego Δτ obliczyłem korzystając z metody różniczki zupełnej:

po podstawieniu i obliczeniu:

Δτ = 1,61 ∙ 10^-6 [min]

Δτ = 0,966 ∙ 10^-4 [s]

ostatecznie:

τ = (3,879 ± 0,966) ∙ 10^-4 [s]

wyliczony błąd Δτ stanowi 24,9 % τ

Kolejnym etapem tego ćwiczenia był pomiar aktywności próbki za pomocą okienkowego licznika G - M. Wyniki, które otrzymałem zawiera tabela 5. Dokładna ich analiza wskazuje na to, iż badany preparat wysyłał promieniowanie beta, gdyż promieniowanie to jonizuje bezpośrednio ośrodek i nie potrzebuje materii (która de facto osłabia je) w oddziaływaniu z którą powstałyby elektrony wtórne powodujące jonizację gazu w komorze licznika. Reasumując gdyby próbka wysyłała kwanty gamma to pomiar wykazałby większą jej aktywność po stronie bez okienek (czyli odwrotnie niż u nas).

Strona	Skala	Wartość [μGy/h]
Bez okienek	60	12
Z okienkami	2400	1400

Następnie przeanalizowałem rozpad promieniotwórczy jako zdarzenie statystyczne i zbadałem jego zgodność z rozkładem Poissona. Od dawna wiadomo, że proces rozpadu promieniotwórczego ma charakter losowy tzn. nie jesteśmy w stanie stwierdzić czy dane jądro ulegnie rozpadowi w danym przedziale czasu, a jedynie możemy podać prawdopodobieństwo zajścia tego zjawiska. Wynika to z faktu że prawa fizyki na poziomie mikroskopowym mają charakter statystyczny. Dlatego też, przy rozpatrywaniu zagadnień związanych z rozpadem jąder posługujemy się statystyką. W naszym przypadku wykorzystamy rozkład Poissona, który opisuje prawdopodobieństwo zajścia n - zdarzeń losowych w N - próbach, pod warunkiem że prawdopodobieństwo zajścia pojedynczego zdarzenia jest stałe i bardzo małe

gdzie:

N - liczba doświadczeń

n - liczba zdarzeń losowych

β - jest iloczynem N i p

Dokonałem pomiarów 300 rozpadów każdy trwający po 0,1 sekundy. Wynikiem jest histogram (wykres nr 2) wraz z obliczeniami wykonanymi przez komputer.

Histogram ten przedstawia zależność pomiędzy intensywnością promieniowania a powtarzalnością intensywności. Widoczna wyraźna choć niezupełna symetria.

# - teoretyczny rozkład Poissona,

* - rozkład zmierzony.

Doświadczalne wartości odbiegają nieco od teoretycznych co najprawdopodobniej spowodowane jest to małą ilością pomiarów, czasem martwym licznika i bezwładnością aparatury liczącej.

Jest to wykres dla czynnika β = 7,496667 wyliczonego według wzoru:

gdzie:

N - Intensywność promieniowania otrzymana w danym pomiarze.

KN - Ilość otrzymanych takich samych intensywności promieniowania.

Komputer wykorzystując rozkład Poissona obliczył prawdopodobieństwo:

Zebrane dane liczbowe pozwalają na wyznaczenie rozbieżności pomiędzy teoretycznym rozkładem P(n) a rozkładem przeprowadzonym na skończonej liczbie zdarzeń zwanym testem X² (X² = 21,11906). Obliczenia wykonane przez komputer zawarte w tabeli nad wykresem Poissona (NT - kolumna zawierająca iloczyn P(n)⋅ n, będący liczbą wystąpienia tej samej intensywności promieniowania w wyniku n /n =300/ pomiarów. Pozostałe wielkości zostały określone w tekście).

Wnioski:

Dzięki przeprowadzonemu ćwiczeniu poznaliśmy budowę oraz zasadę działania i praktyczne zastosowanie licznika G - M.

Mogliśmy nauczyć się sposobu pomiaru tym licznikiem co może przydać się nam na wyższych latach studiów lub na innych przedmiotach wykładanych na uczelni. Ponadto przypomnieliśmy sobie podstawowe pojęcia z rachunku prawdopodobieństwa, oraz rozkład Poissona, z którym mieliśmy styczność na niższym roku studiów w Laboratorium Fizyki I.

8

---