33.a) W jaki sposób oblicza się całkę krzywoliniową skierowaną na płaszczyźnie i w przestrzeni? Twierdzenie Greena i twierdzenie Stokesa-Ostrogradskiego.

W R² ( w R³ , odpowiednio) dany jest łuk zwykły:

Zakładamy, że opis Φ ma kierunek zgodny ze wzrostem parametru.

Uwaga: a) Istnieje nieskończenie wiele opisów, których kierunek jest zgodny ze wzrostem parametru t.

b) Jeżeli opis Φ (np. w R²) jest „zgodny”, to opis

Zakładamy, że w R² (R³) dane jest ciągłe pole wektorowe

Przedział parametrów <α;β> dzielimy na n podprzedzialików α=t₀<t₁<...<t_n-1<t_n=β.

Punktowi t_i podziałowi odpowiada punkt A_i = Φ(t_i), i=0,1,2,...,n na łuku AB

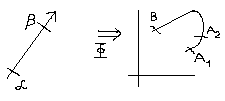
W każdym przedziale <t_k-1;t_k> obieramy w dowolny sposób punkt pośredni γ_k, k=1,2,...,n-1.

Punktowi γ_k odpowiada punkt Φ(γ_k )=( φ_k ;η_k) ( Φ(γ_k )=( φ_k ;η_k;ξ_k) ) leżący na łuku A_kB_k ( 0≤ k ≤ n). Przypisujemy

Piszemy sumę całkową w postaci

Definicja: Jeżeli dla każdego normalnego ciągu podziałów przedziału <α; β> ciąg sum jest zbieżny do tej samej granicy właściwej, niezależnie od wyboru punktów, to tę granicę nazywamy całką krzywoliniową skierowaną pary funkcji [P(x, y); Q(x, y)] po łuku AB i oznaczamy symbolem

Tw. Green'a

Jeżeli pole wektorowe
jest klasy C¹ w obszarze D⊃R² normalnym względem OX i OY, a brzeg ∂D jest skierowany dodatnio względem wnętrza obszaru, to

Twierdzenie (o niezależności całki krzywoliniowej od kształtu drogi całkowania)

Jeżeli pole wektorowe
jest klasy C¹ w obszarze jednospójnym D, to całka krzywoliniowa skierowana po łuku kawałkami gładkim ABCD nie zależy od drogi

tw. Stokesa-Ostrogradskiego

Określa ono zależność pomiędzy strumieniem rotacji pola A (ciągłego wraz z pochodnymi cząstkowymi w każdym punkcie rozważanego obszaru) przenikającym powierzchnię S, a cyrkulacją tego pola po konturze C, stanowiącym krawędź tej powierzchni.

33.b) Obliczyć całkę
, gdzie ၫ jest krzywą o równaniu |x|+|y|=1 skierowaną dodatnio względem wnętrza.

.

K: |x|+|y|=1

Q(x,y)=P(x,y)=

-1

-1

1

1

x

y

---