Zestaw 3.

1. Co to jest operacja elementarna algorytmy? Przykład

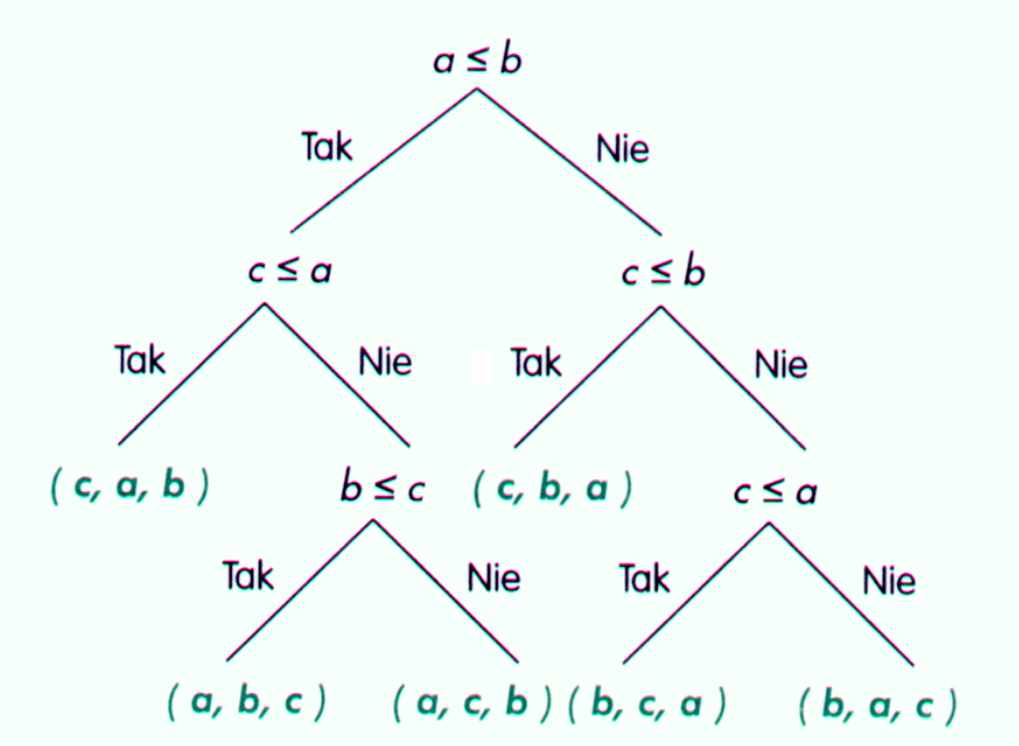
2. Naszkicuj drzewo alg. Sortowania trzech liczb

3. Jaką złożoność czasową posiada alg. Sortowania przez scalanie. Opisz ta złożoność.

4. opisz alg. Sprawdzania czy punkt należy do wielokąta wypukłego

5. Lista kroków sortowania stogowego

6. Definicja listy

7. Definicja stosu

8. Drzewo binarne BST

9. Macierz incydencji. Złożoność początkowa

10. Przykład alg Kruskala i kroki

1. * - + i tak daej

2. sortowanie 3 liczb -> schemat

3. Liczbę porównań sortowania przez scalanie można wyzbaczyc kozystajac z jego postaci. Oznaczmy te liczbe jako r(n) i załóżmy ze n jest potega liczby 2 czyli n=2k dla danej liczby k. Otrzymujemy wówczas nastepujaca zależność rekurencyjna: r(n)=0 dla n=1; r(n)=1 dla n=2; r(n)=2r(n/2)+(n-1) dla n>2; Gdy n=1 nie wykonujemy zadnego porównania gdy n=2 wykonujemy jedno porównanie podczas scalania ciągów jednoelementowych, gdy n>2 wykonujemy 2 razy porządkowanie ta sama metoda ciągów o polowe krótszych oraz scalamy te ciagi wykonując co najwyżej n-1 porownan (o jedno mniej niż jest elementow w obu podciągach).

5. 
   Lista krokow:
   
   1 Dana jest tablica A[1..n] będąca kopcem, wobec tego element A[1] jest maksymalny.
   2 Niech m oznacza ostatni element kopca; na początku kopiec obejmuje całą tablicę, więc m jest równe n.
   3 Zamień ze sobą elementy A[1] i A[m].
   4 Zmniejsz m o 1.
   5 Przywróć własność kopca dla tablicy A[1..m] zaczynając od elementu A[1].
   6 Wróć do kroku 3]

6. Lista - uporzadkowany ciag elementow, przykladami list sa wektory lub tablice jednowymiarowe. W wektorach mamy dodstep do elementu poprzez podanie indeksu elementu. Lista to liniowo uporzadkowany zbior elementow z których dodolny element można usunac lub dodac w dowolnym miejscu, piwrwszy i ostatni elemenet listy nazywamy koncami listy. Szczegolne przypadki list Stos i kolejka.
   Listy dziela się na: posortowane i nieposortowane.
   Lista jednokierunkowa jest oszczedna pamieciowa struktura danych pozwalajaca grupowac dodolna - ograniczona iloscia dostepnej pamieci. Do budowy list jednokierunkowej uzywane sa dwa typy komorek Pamieci. Pierwszy jest zwyklym rekordem natury informacyjnej, drugi jest rekordem lecz ma on charakter roboczy.
   Wlasnosci listy jednokierunkowej: Jeżeli list jest pusta to strukt. Informacyjna zawiera dwa wskazniki null.
   Podczas dołańczania nowego el. Do listy jednokier. Możliwe sa dwa podejscia: Liste traktujemy jako worek; lista jest nieuporzadkowana; nowe elementy będą na liscie we wlasciwej kolejnosci.
   Dodawanie el. Do listy jednokier. Do posortowanej:Nowy element może zostac wstawiony na poczatek, koniec lub w srodku listy posortowanej;;; należy znalezc miejsce wstawienia;
   Dekrementacja- jest to usuwanie ostatniego el z listy jednokier.
   Listy dwukierunkowe: maja dwa wskazniki co przyspiesza wszystkie operacje.

7. Stos- liniowa struktura danych dostepna do zapisywania, odczytywania tylko konca wierzcholka. Struktura LIFO.
   Operacje na stosie: initializa, oroznienie stosu, empty sprawdzenie stosu czy jest pusty, full- sprawdzenie stosu czy jest zapelninony, push- umieszczenie elementu na stosie, pop- zdjecia najwyzszego el ze stosu.

8. Drzewo BST (Binary Serach Tree) jest drzewem binarnym. Oprocz pola wartości BST posiada jeszcze 2 pola L i P wskazujące na lewy i prawy następnik. Drzewo BST ma szczegolna własność: jeżeli element drzewa znajduje się w lewej galezi to jest mniejszy od swojego poprzednika jeżeli element znajduje się w prawej kawedzi jest od poprzednika wiekszy. Przeszukiwanie drzewa: wzdłużna - preorder - korzen, lewe poddrzewo, prawe poddrzewo; poprzeczna - inorder - lewe poddrzewo, korzen, prawe poddrzewo; wsteczne - postorder - lewe poddrzewo, prawe poddrzewo, korzen.

9. Macierz incydencji to tablica o rozmiarach V*E. Sklada się z E kolumn i V wierszy
   - jeśli krawędź wychodzi z danego wierzcholka to piszemy w odpowiedniej kolumnie l-1
   -jeśli do niego wchodzi piszemy l+1
   jeśli wierzcholek nie należy do krawędzi piszemy 0
   jeśli jest to petla wlasna piszemy 2
   Macierz grafu: tablica o rozmiarach (V+2)^2. Wierzcholki i krawędzie numerujemy od 0 do v+1

10. ALG. KRUSKALAPolega na laczeniu wielu poddrzew w jedno za omoca krawędzi o najmniejszej wadze. W rezultacie powstałe drzewo będzie minimalne. Algorytm oparty jest na metodzie zachlannej
    Kroki dla K;
    -posortowac wszystkie krawędzie w porządku niemalejącym
    -tworzenie drzewa - rozrastanie lasu drzew
    -wybieramy krawędzie o najmniejszej wadze i jeśli wybrana krawędź należy do dwoch roznych drzew należy je scalic (dodac do lasu)
    -krawedzie wybieramy tak dlugo Az wszystkie wierzcholki nie będą należały do jednego drzewa

---