Wydział Elektryczny Politechniki Szczecińskiej

Elektronika i Telekomunikacja

Oscyloskop jako przyrząd pomiarowy

Oscyloskop jest elektronicznym przyrządem umożliwiającym wyświetlanie wykresu dwu lub większej liczby współbieżnych w czasie przebiegów elektrycznych. Najczęściej oscyloskop używany jest do przedstawiania wartości sygnałów na osi pionowej w zależności od czasu podawanego na osi poziomej. Na lampie oscyloskopowej zamontowana jest podziałka, która w przybliżeniu wyskalowana jest w centymetrach. Z podziałki tej odczytujemy wartości przez nas mierzone. Błędy jakie występują przy pomiarze wartości to błędy odczytu z podziałki, oraz błędy wynikające z własności przyrządu (uchyb liniowości wzmacniaczy odchylania, uchyb liniowości generatora podstawy czasu, uchyb kalibracji). W typowym oscyloskopie laboratoryjnym dla obrazu przebiegu o wysokości 5 cm przyjmuje się uchyb maksymalny, składający się z:

- uchybu paralaksy: od 0 do -2%,

- uchybu odczytu wysokości: (±0,5 mm/50 mm) * 100% = ±1%,

- uchybu kalibratora napięcia ±2%,

- uchybu tłumika ±2%, co razem daje uchyb od -7% do +5%.

Aby w pomiarze oscyloskopem wartości miały jak najmniejszy błąd pomiaru, obraz mierzonego przebiegu powinien zająć maksymalną wysokość ekranu; z pomiaru należy wyeliminować grubość linii, oraz stale odczytując wartości odchylania w kierunku pionowym przy tej samej krawędzi linii obrazu; oscyloskop powinien być wykalibrowany; napięcie sieci zasilającej i pokrętła mające wpływ na pomiary powinny być ustawione zgodnie z instrukcją obsługi; sonda powinna być prawidłowo skompensowana, jak również należy pamiętać o wpływie szerokości pasma przenoszenia wzmacniacza na dokładność pomiaru przebiegów o różnych częstotliwościach.

Przy pomiarze kąta przesunięcia fazowego, oraz stosunku częstotliwości wykorzystuje się metodę figur Lissajous. Figury Lissajous stosuje się w pomiarach oscyloskopowych głównie w pomiarach różnic kąta fazowego i pomiarach stosunku częstotliwości. Popularną metodą pomiaru kąta fazowego jest pomiar parametrów figury uzyskanej na ekranie, gdy do obu par płytek odchylania pionowego i poziomego doprowadzimy napięcia sinusoidalne. Jeżeli stosunek częstotliwości f₁ i f₂ obu sygnałów jest równy stosunkowi liczb całkowitych m:n, to na ekranie oscyloskopu otrzymuje się złożoną figurę nieruchomą, zwaną figurą Lissajous. Na podstawie kształtu tych figur możemy określić stosunek częstotliwości obu sygnałów i początkową różnicę faz. Z pomiaru parametrów elipsy uzyskanej dla dwu przebiegów sinusoidalnych o tej samej częstotliwości możemy obliczyć kąt przesunięci fazowego.

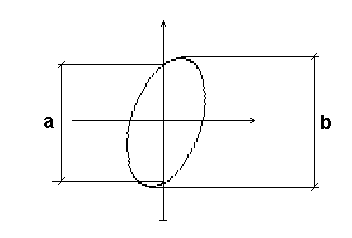
Przy pomiarze częstotliwości, jeżeli stosunek obu częstotliwości jest równy stosunkowi dwu liczb całkowitych, to otrzymuje się na ekranie krzywą zamkniętą, jeżeli dodatkowo kąt przesunięcia fazowego między nimi jest stały w czasie to otrzymamy obraz nieruchomy. Stosunek obu częstotliwości oblicza się ze stosunku liczby przecięć prostej pionowej z obrazem do liczby takich przecięć prostej poziomej. Obie proste powinny być tak przeprowadzone, aby nie były styczne i nie przechodziły przez punkty węzłowe obrazu. Stosunek obu częstotliwości oblicza się ze wzoru

gdzie: P_x - liczba przecięć figury z prostą poziomą;

P_y - liczba przecięć figury z prostą pionową.

Wykaz przyrządów wykorzystanych w ćwiczeniu:

Oscyloskopy:

• ST-315A II

• OS-301

• OS-351

• OS-351

Generatory funkcyjne:

• KZ-1406;

• PO-27;

• POF-10

• POF-10

Wyznaczanie niepewności odczytu w pomiarze napięcia międzyszczytowego oscyloskopem:

Niepewność bezwzględna odczytu

< l_x > - grubość linii;

Niepewność względna odczytu:

Niepewność bezwzględna pomiaru napięcia:

Tabela pomiarów i obliczeń:

Pomiar amplitudy:

Typ oscyloskopu	Współcz. kalibracji	Bezwzględnaniepewność odczytu	Odległość między-szczytowa napięcia	Niepewność względna odczytu	Wartość napięcia Między-szczyt.	Wartość napięcia szczyt.	Niepewność bezwzgl. pomiaru napięcia	Wynik wraz z niepewnością
Symbol	Cy	<lx>	lx	<δlx>	Uxm	Ux	<Ux>
OS-301	5 V/dz	0,3 dz	8,3 dz	≈3,6%	41,5 V	20,8 V	1,5 V	(20,8 ± 1,5) V
OS-351	2 V/cm	0,05 cm	5,00 cm	≈1,0%	10,0 V	5,0 V	0,1 V	(5,0 ± 0,1) V
OS-351	2 V/cm	0,1 cm	4,8 cm	≈2,1%	9,6 V	4,8 V	0,2 V	(4,8 ± 0,2) V

Pomiar częstotliwości:

Typ oscyloskopu	Podstawa Czasu	Długość Okresu	Niepewność względna odczytu	Wartość Okresu	Częstotli- Wość	Wartość Błędu	Wynik wraz z niepewnością
Symbol	u/cm	Tx	<δTx>	s	KHz	Hz
OS-351	20us/cm	4,65 cm	≈3%	0,000093	10,752	322	(10752 ± 322)Hz
OS-351	20us/cm	3,82 cm	≈3%	0,0000764	13,089	393	(13089 ± 393) Hz

Wnioski:

W pomiarach zauważyliśmy, że przy bardzo wysokich częstotliwościach, sygnał wejściowy był deformowany przez układ wejściowy oscyloskopu. Z przebiegu łatwo się było domyślić, że jest to układ o właściwościach filtru górnoprzepustowego. Efekt był wyraźnie widoczny przy obserwowaniu przebiegu prostokątnego, ów który zbliżał się wyglądem do sinusoidy.

Nasz zespół chciał wyliczyć kąt przesunięcia fazowego dwóch częstotliwości, jednak metoda figur Lissajous nam tego nie umożliwiła. Przyczyną były ciągłe oscylacje figur, spowodowane niestabilnością generowanej częstotliwości, jak również oprzyrządowaniem (lekkie trącenie kabla zakłócało przebieg).

Przy pomiarze częstotliwości stwierdziliśmy, że ów pomiar odczytywany i obliczenia nie są zadowalające dla dużych częstotliwości(stopa błędu sięga 3%). Jeżeli chcielibyśmy np. pomierzyć nośną generowaną przez dowolny układ radionadajnika (rzędu Mhz), odczyt musiałby być w miarę dokładny, aby stwierdzić czy generowana częstotliwość nie dryfuje. Jak widzimy do tego celu lepiej jest używać częstościomierzy, a dobrze jest wiedzieć, że oscyloskop poza wyświetlaniem przebiegu badanego ma też inne możliwości, między innymi właśnie takie.

---