Rozwiązania zadań B.5

Agnieszka Krawacka

1

DOSKONAŁA KONKURENCJA 1

Zadanie 1 (1 B.5)

a)

Pole prostokąta c g o i

b)

Pole prostokąta d f c g

c)

Cena p należy do [0, a)

d)

Pole prostokąta d*j

e)

P = b

Zadanie 2 (2 B.5)

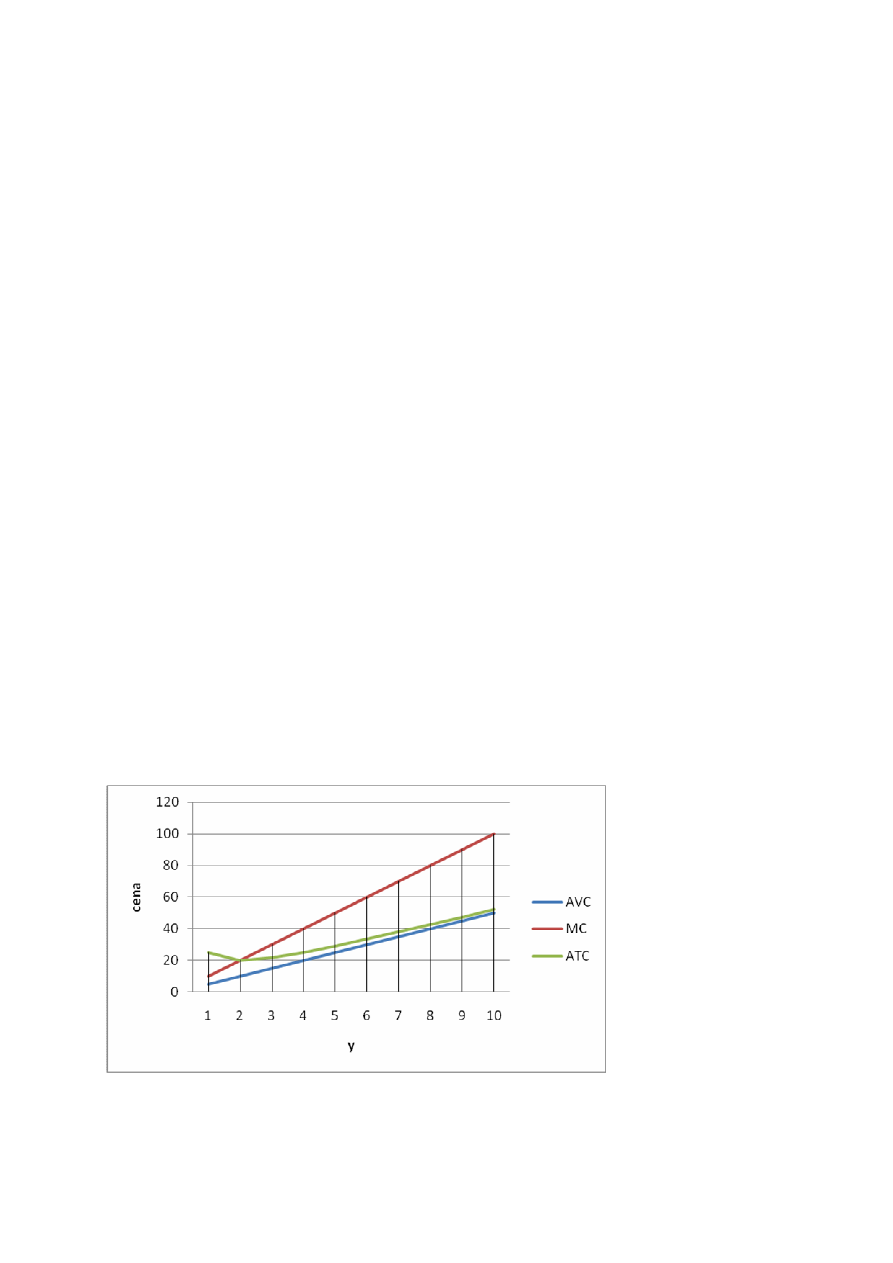
TC(y)= 5y

2

+20

AC(y)= 5y+20/y

MC(y)= 10y

P=MC => p=10y => y=p/10

MC=AC

5y+20/y=10y => 20/y=5y => 5y

2

=20 => y=2

AC= 5*2+20/2= 20 => cena=20

funkcja podaży

p=10y dla p≥20

y=0 dla p<20

Zadanie 3 (3 B.5)

Q= n*y= n*p/10

Rozwiązania zadań B.5

Agnieszka Krawacka

2

AVC=5y => y

min

=0

Zadanie 4 (5 B.5)

TC(q)= 3q

3

-6q

2

+28q+72

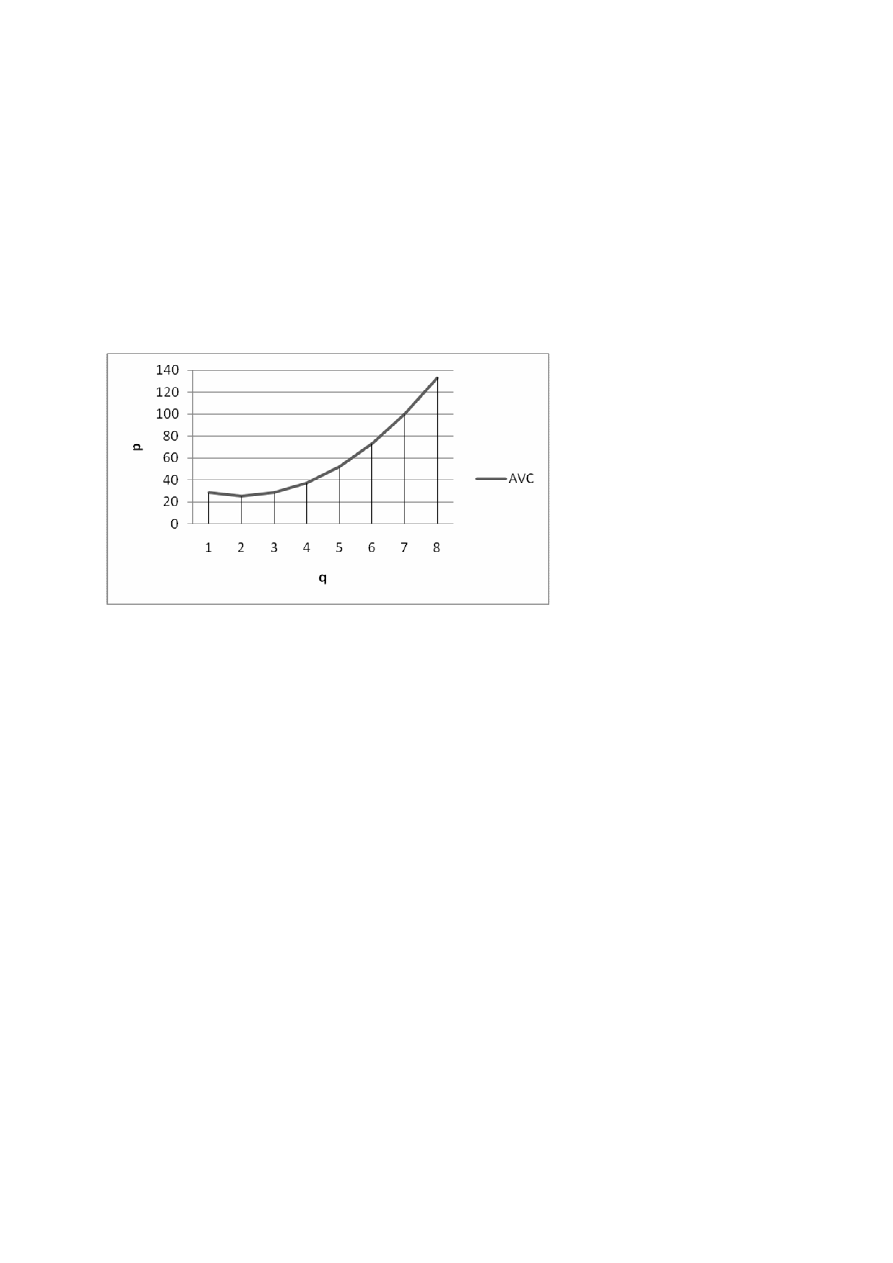
Firma produkuje gdy p≥min AVC(q), nie produkuje gdy p< min AVC(q)

AVC(q)= 3q

2

-6q+28 – min <=> 6q – 6 = 0 <=> q=1

AVC(1)=25. Czyli firma nie produkuje, dla p

∈

[0,25)

Funkcja podaży

P=9q

2

-12q+28 dla p≥25

Q=0 dla p<25

Czyli:

Q=2/3+1/3(p-24)

0,5

dla p≥25

Q=0 dla p<25

Zadanie 5 (6 B.5)

Q= 2 L

0,5

Π= pq-TC(q)

Π= pq(L)-wL

wL=TC =>

(

w*q

2

)

/4=TC

MC(q)= w/2*q => p=MC => p=

(

w/2

)

*q

Q(p)= 2p/w

Rozwiązania zadań B.5

Agnieszka Krawacka

3

Zadanie 6 (4 B.5)

Q(p)= 100p

FC=30 n=200

Q= 100p/200=1/2*p

Dla jednej firmy p=2q=MC

TC(q)=q

2

+30

Zadanie 7 (3.4.2 B.5)

P=1,5

a)

TC=0,5x+0,1xn => n= ilość kilometrów, x= ilość kilogramów

Π=1,5x-0,5x-0,1xn= x-0,1xn

b)

Π≤0

x-0,1xn≤0 /:x x>0

1-0,1n≤0

1≤0,1n

n≥10

Zadanie 8 (3.4.8 B.5)

f(L)=6L

2/3

P=3 w=6

P*MP

L

=w

3*6*2/3*L

-1/3

=6 => L=8

f(8)=6*8

2/3

=6*4=24

Π= p*f(8)-wL= 3*24-6*8=72-48=24

Zadanie 9 (3.4.22 B.5)

Q= f(s)=3*s

2/3

p=50 w=20

Π=50*3*s

2/3

-20s

P* MP

s

= w => 50*3*2/3*s

-1/3

=20 => s=125

Q= 3*125

2/3

=3*25=75

Rozwiązania zadań B.5

Agnieszka Krawacka

4

Π=50*75-20*125=1250

Łasuch zużyje 125 smurfojagód wytwarzając 75 słoików dżemu, a jego maksymalny zysk wyniesie
1250 szł.

Zadanie 10 (15 B.5)

TC

1

=100+2q

1

2

/1000 p=1

TC

2

=200+2q

2

2

/1000

TC

3

=100+q

3

2

/1000

a)

MC

1

= MC

2

= MC

3

=p

b)

MC

1

=

(

1/250

)

*q

1

MC

2

=

(

1/250

)

*q

2

MC

3

=

(

1/500

)

*q

3

MC= p

q

1

=250 q

2

=250 q

3

=500

TC=TC

1

+TC

2

+TC

3

=400+q

2

/2000

←

←

←

←

powinno być 200

MC= q/1000=1 => q=1000

←

←

←

←

powinno być MC=q/100=1 => q=100

Π=pq-400-q

2

/2000

←

←

←

←

powinno być Π=pq-400-q

2

/200

Π=1000-400-1000

2

/2000=100 – o ile opłaca się produkować we wszystkich fabrykach.

←

←

←

←

powinno być Π=100-400-100

2

/200=-350

c)

q

1

=250 => Π

1

=250-100-2*250

2

/1000=25

q

2

=250 => Π

2

=250-200-2*250

2

/1000=-75 nie opłaca się w tej fabryce produkować

q

3

=500 => Π

3

=500-100-500

2

/1000=150

Π= Π

1

+ Π

2

=25+150=175

Zysk z produkcji z trzech fabrykach jest mniejszy niż tylko w pierwszej i trzeciej.

Zadanie 11 (5 B.5)

C(q)=STC=

(

1/300

)

*q

3

+0,2q

2

+4q+10

a)

AVC=q

2

/300+0,2q+4 => minAVC=-b/2a => minAVC<0

AVC(0)=4

MC=q

2

/100+0,4q+4

Funkcja podaży

P= q

2

/100+0,4q+4 dla p≥4

Q=0 dla p<4

b)

100p=q

2

+40+400

Rozwiązania zadań B.5

Agnieszka Krawacka

5

100p=(q+20)

2

(100p)

1/2

=q+20

q=(100)

1/2

-20

Q=n*q=100*p

1/2

-2000

c)

100*p

1/2

-2000=-p/20+55

100*p

1/2

=-p/20+2055

t=p

1/2

=> t

2

/20+100t-2055=0

t

2

+2000t-41100=0

t

1

≈20,343

t

2

= <0

p=t

2

=> p≈413,84

Q

S

*=Q

D

*=34,3