Materiały pochodzą z Platformy

Edukacyjnej Portalu

www.szkolnictwo.pl

Wszelkie treści i zasoby edukacyjne publikowane na łamach Portalu www.szkolnictwo.pl mogą być wykorzystywane przez jego
Użytkowników

wyłącznie

w zakresie własnego użytku osobistego oraz do użytku w szkołach podczas zajęć dydaktycznych. Kopiowanie, wprowadzanie zmian,
przesyłanie,

publiczne

odtwarzanie

i wszelkie wykorzystywanie tych treści do celów komercyjnych jest niedozwolone. Plik można dowolnie modernizować na potrzeby
własne

oraz

do

wykorzystania

w szkołach podczas zajęć dydaktycznych.

„Po co ludzie uczą się

matematyki? Żeby uczyć

matematyki innych.”

Hugo Steinhaus

ROZWIĄZYWANIE UKŁADÓW

RÓWNAŃ – METODA

PODSTAWIANIA.

Istnieje wiele metod rozwiązywania układów
równań, jedną z nich jest metoda
podstawiania. Aby nauczyć się rozwiązywać
układy dwóch równań z dwiema
niewiadomymi, musisz umieć rozwiązywać
równania z jedną niewiadomą.

METODA PODSTAWIANIA

Rozwiązywanie układów równań metodą
podstawiania polega na wyznaczeniu z
jednego z równań jednej z niewiadomych i
podstawieniu jej do drugiego równania. W
ten sposób otrzymujemy równanie z jedną
niewiadomą.

UWAGA

Staraj się zawszę wyznaczyć tą niewiadomą,
która jest łatwiejsza do wyznaczenia.
Zawsze poszukuj optymalnej drogi do
rozwiązania.

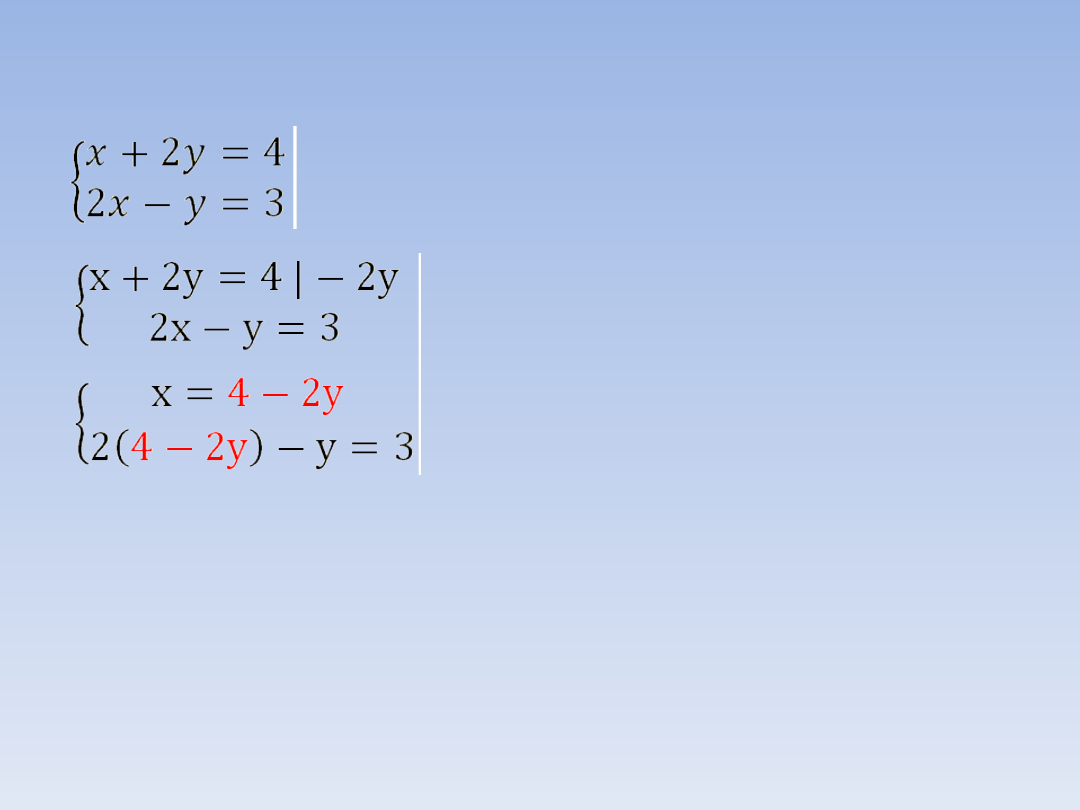
PRZYKŁADY.

PRZYKŁAD 1.

2(4 – 2y) – y = 3
8 – 4y – y = 3
-5y = 3 – 8
-5y = -5 | :(-5)
y = 1

Pierwsze równanie przekształcamy tak, aby
wyznaczyć z niego x.

Z pierwszego równania wyznaczamy x i
podstawiamy otrzymane wyrażenie w
miejsce x do drugiego równania.

Rozwiązujemy otrzymane równanie z jedną
niewiadomą (y).

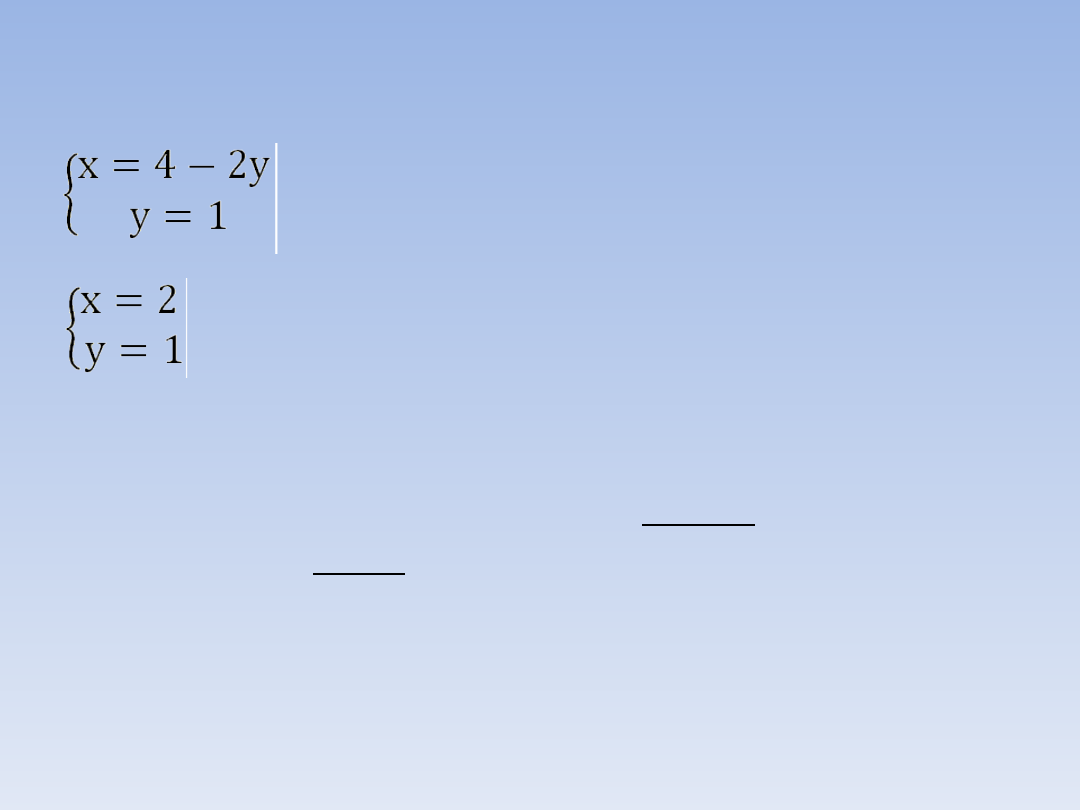
PRZYKŁADY.

PRZYKŁAD 1 – ciąg dalszy.

UWAGA

Powyższy układ równań ma jedno rozwiązanie,
którym jest para liczb x = 2 i y = 1.
Te dwie liczby stanowią jedno rozwiązanie
układu równań, gdyż jednocześnie spełniają
oba równania tego układu.

Aby obliczyć wartość x wstawiamy y = 1 do
równania x = 4 – 2y

Rozwiązaniem układu równań jest para liczb x = 2 i y
= 1.

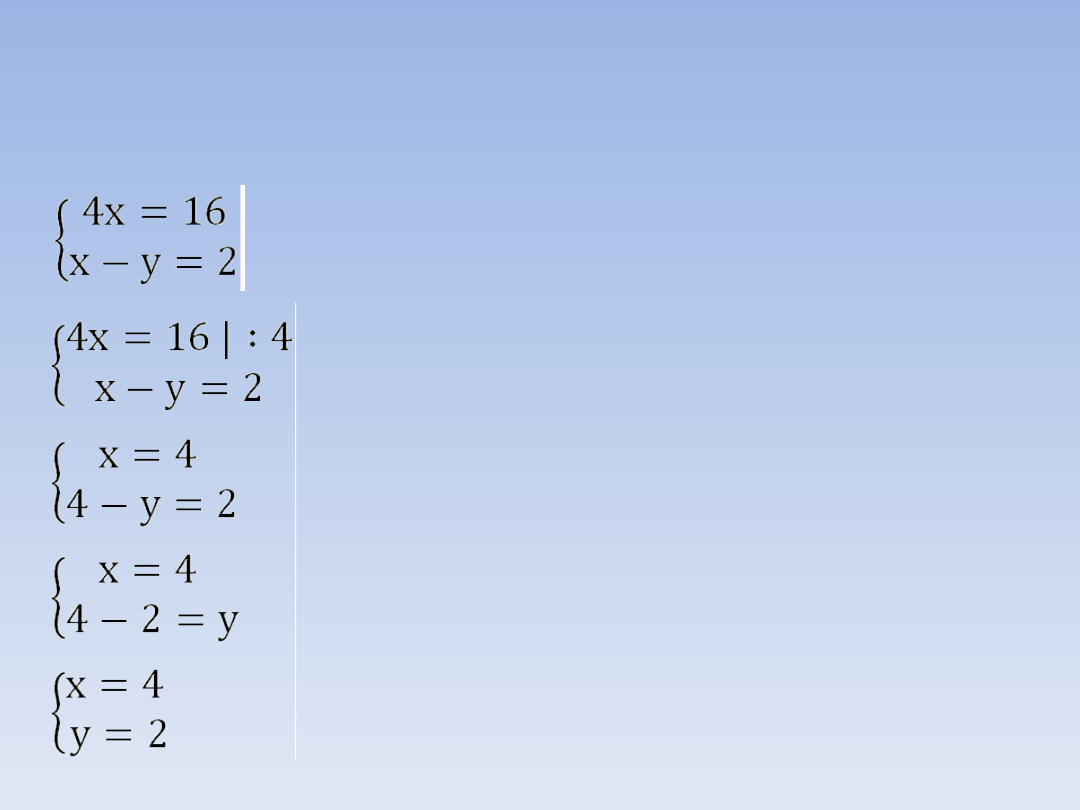
PRZYKŁADY.

PRZYKŁAD 2.

Z pierwszego równania wyznaczamy x i
podstawiamy otrzymane wyrażenie w
miejsce x do drugiego równania.

Rozwiązujemy otrzymane równanie z jedną
niewiadomą (y).

Rozwiązaniem układu równań jest para liczb x =
4 i y = 2.

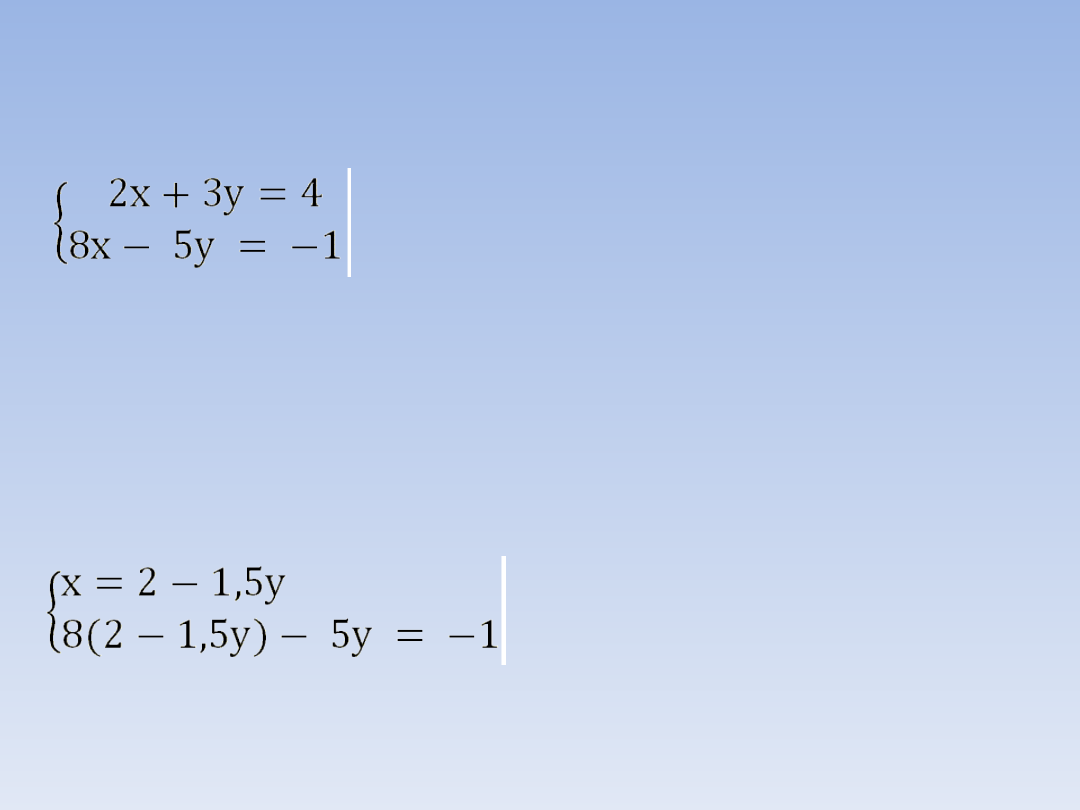
PRZYKŁADY.

PRZYKŁAD 3.

2x + 3y = 4 | -3y

2x = 4 – 3y | :

2

x = 2 – 1,5y

16 – 12y – 5y = -1

Z pierwszego równania wyznaczamy x i
podstawiamy otrzymane wyrażenie w
miejsce x do drugiego równania.

Rozwiązujemy otrzymane równanie z jedną
niewiadomą (y).

Wyznaczone x.

Podstawiamy wzór na x do drugiego
równania.

PRZYKŁADY.

PRZYKŁAD 3 – ciąg dalszy.
16 – 12y – 5y = -1
-17y = -1 – 16
-17y = -17 | :

(-17)

y = 1

Aby obliczyć wartość x wstawiamy y = 1 do
równania
x = 2 – 1,5y

Rozwiązaniem układu równań jest para liczb x = 0,5 i
y = 1.

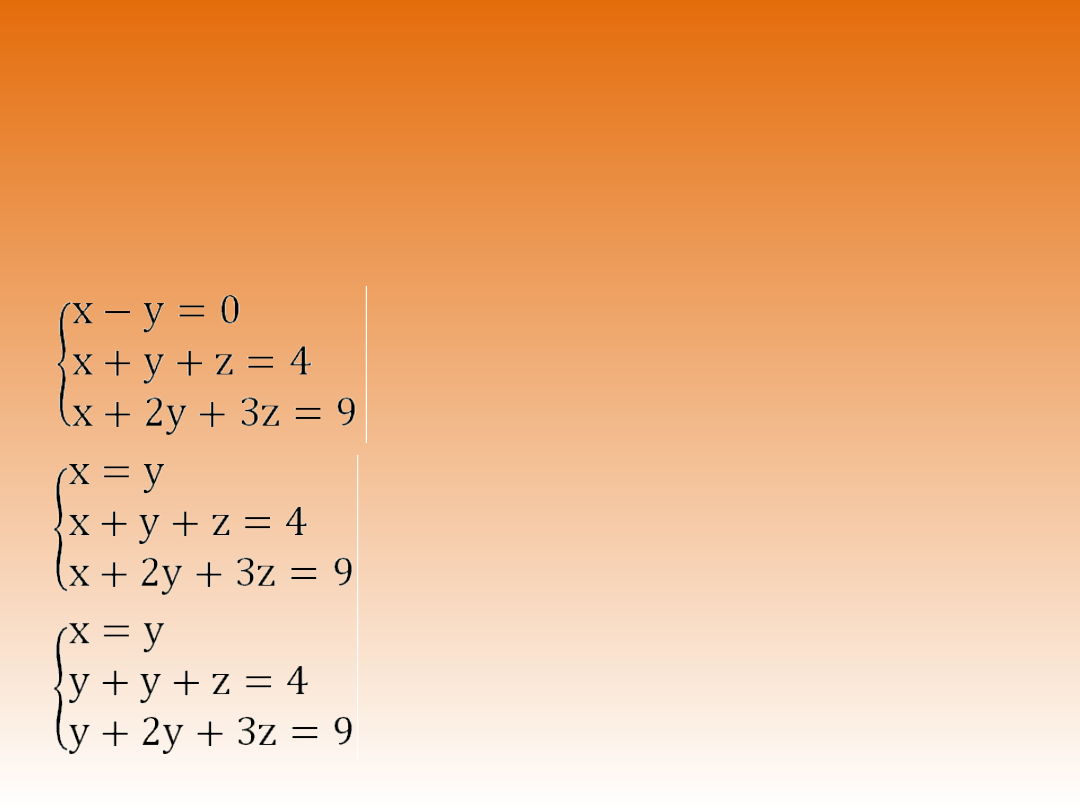
PRZYKŁADY.

PRZYKŁAD 4.
Oto zastosowanie metody podstawiania do

rozwiązania prostego układu trzech
równań z trzema niewiadomymi.

Z pierwszego równania wyznaczamy x.

Podstawiamy x do drugiego i trzeciego
równania otrzymując w ten sposób układ
równań z dwiema niewiadomymi – y i z.

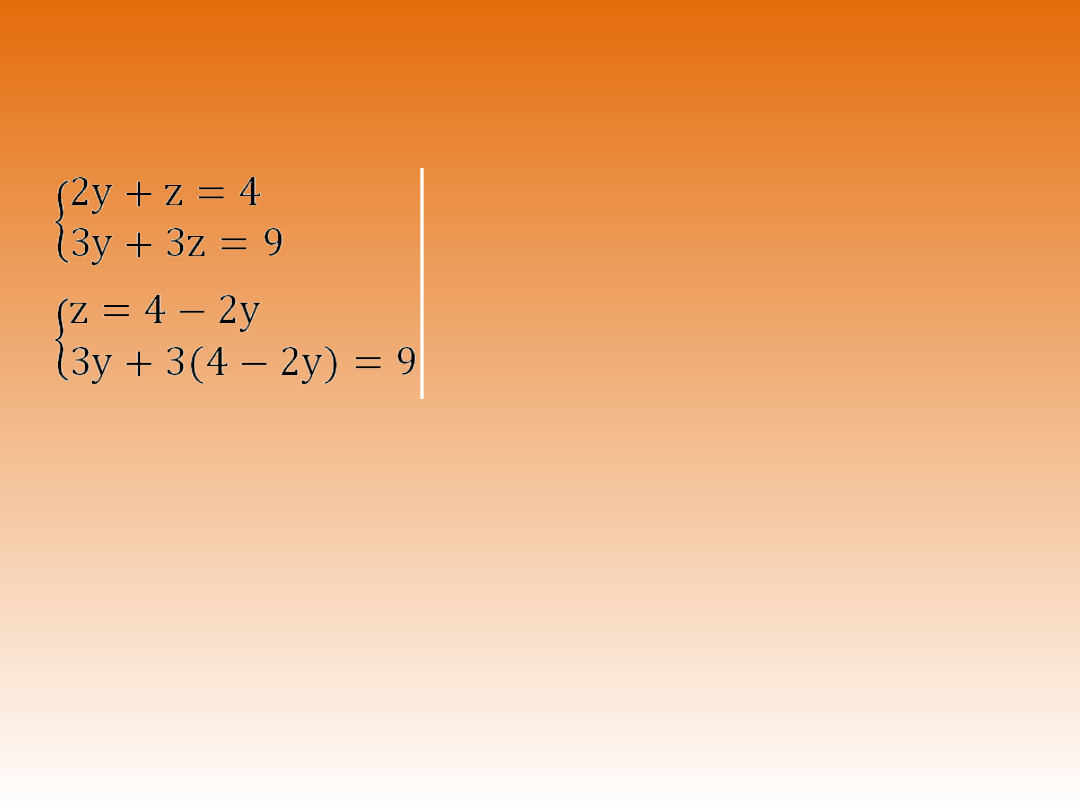
PRZYKŁADY.

PRZYKŁAD 4 – ciąg dalszy.

3y + 12 – 6y = 9
3y – 6y = 9 – 12
-3y = -3 |:

(-3)

y = 1
z = 4 – 2 ∙ 1 = 2
x = 1

Rozwiązujemy układ dwóch równań, z dwiema
niewiadomymi. Na początek z pierwszego równania
wyznaczamy z.

Podstawiamy z do drugiego równania.

z oraz x obliczamy z wyznaczonych
wcześniej wzorów.

PRZYKŁADY.

PRZYKŁAD 4 – ciąg dalszy.

Rozwiązaniem układu jest trójka liczb

spełniających jednocześnie wszystkie trzy
równania: x = 1, y = 1 i z = 2.

Zapisujemy rozwiązanie.