„Jasiu, zostaw kobiety, a 

weź się do matematyki.”

Słowa Zulietty,

 XVIII-wiecznej kurtyzany 

weneckiej,

 skierowane do Jana Jakuba 

Rousseau.

ROZWIĄZYWANIE UKŁADÓW 

RÓWNAŃ – METODA 

PRZECIWNYCH 

WSPÓŁCZYNNIKÓW.

Z  tej  lekcji  dowiesz  się  jak  rozwiązać  układ 
równań metodą przeciwnych współczynników. 
Każdy układ równań da się rozwiązać metodą 
podstawiania,  czasem  jednak  zajmuje  ona 
sporo  czasu.  Często  się  zdarza,  że  metoda 
przeciwnych  współczynników  jest  mniej 
pracochłonna. 

METODA PRZECIWNYCH 

WSPÓŁCZYNNIKÓW

Rozwiązywanie  układów  równań  metodą 
przeciwnych  współczynników  polega  na 
takim  przekształcaniu  obu  równań,  ab  przy 
jednej  z  niewiadomych  uzyskać  te  same 
współczynniki  liczbowe  ale  o  przeciwnych 
znakach.  Dzięki  takiemu  zabiegowi,  po 
dodaniu  do  siebie  obu  równań  stronami, 
jedna 

z 

niewiadomych 

„znika” 

i 

otrzymujemy równanie z jedną niewiadomą. 

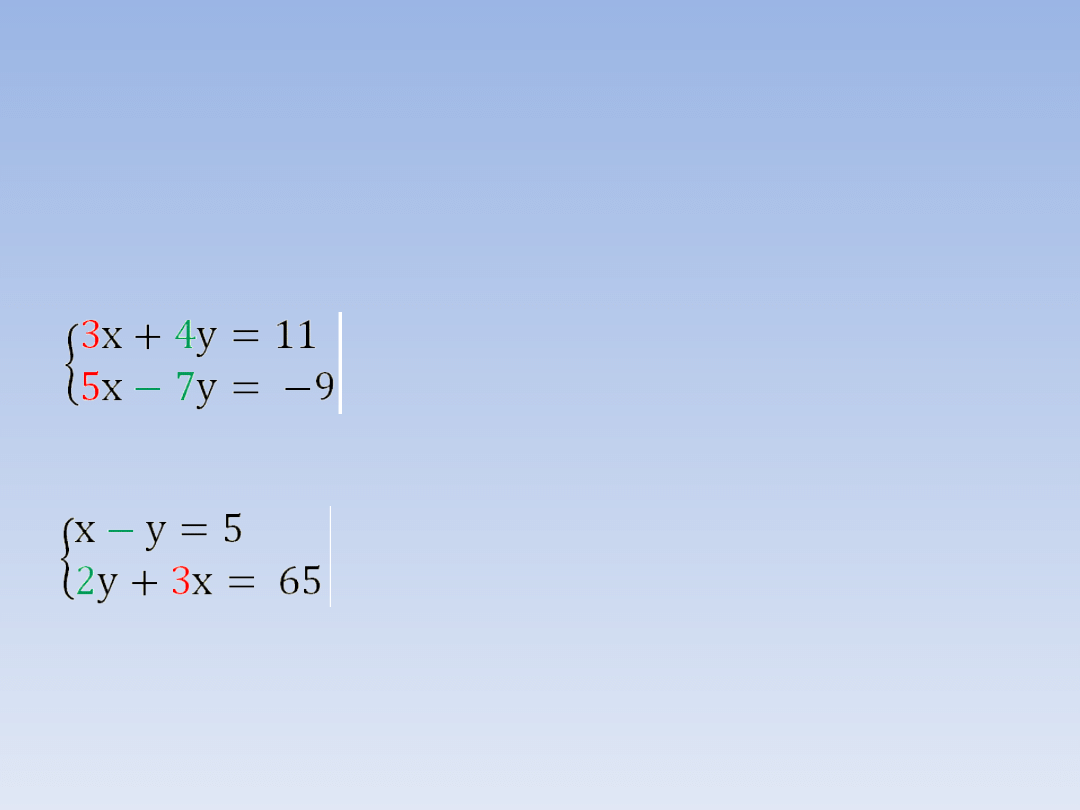
WSPÓŁCZYNNIKI

Czym  są  współczynniki  liczbowe  w  układzie 
równań? 

To 

liczby 

stojące 

przed 

niewiadomymi.
Przykłady:

Współczynniki przy x to: 3 w pierwszym równaniu i 5 w drugim 
równaniu. Współczynniki przy y to: 4 w pierwszym równaniu i 
-7 w drugim.

Współczynniki przy x to: 1 w pierwszym równaniu i 3 w drugim 
równaniu. Współczynniki przy y to: -1 w pierwszym równaniu i 
2 w drugim.

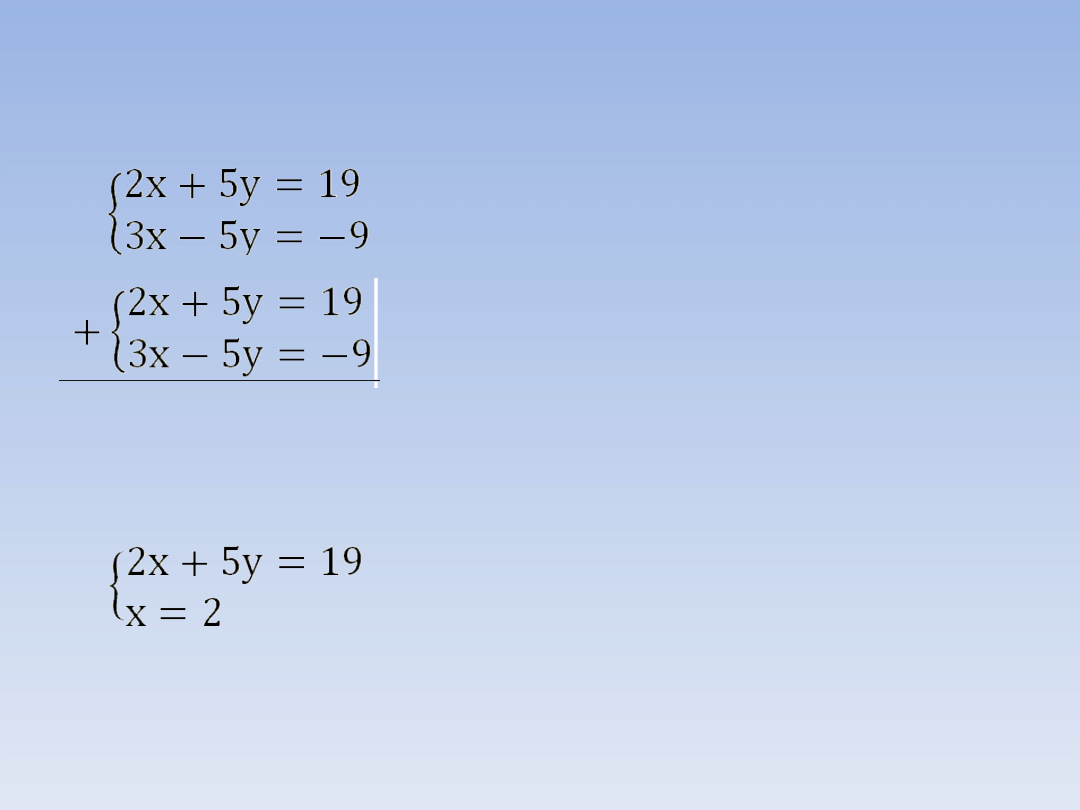
PRZYKŁADY.

PRZYKŁAD 1.

5x = 10 |:

 

5

x = 2

2 ∙ 2 + 5y = 19
4 + 5y = 19

Tego układu równań nie musimy 
przekształcać gdyż współczynniki przy y są 
liczbami przeciwnymi: 5 i -5.

Dodajemy do siebie prawe i lewe strony 
obu równań. Dzięki temu otrzymamy 
równanie z jedną niewiadomą: 5y + (-5y) = 
0
Rozwiązujemy otrzymane równanie z jedną 
niewiadomą (x).

Obliczoną niewiadomą x = 2 wstawiamy 
do jednego (dowolnego) równania układu i 
obliczamy drugą niewiadomą

PRZYKŁADY.

PRZYKŁAD 1 – ciąg dalszy.
5y = 19 – 4
5y = 15 | :

 

5

y = 3

Rozwiązaniem tego układu równań jest para liczb 
x 

= 

2 

i 

y = 3.

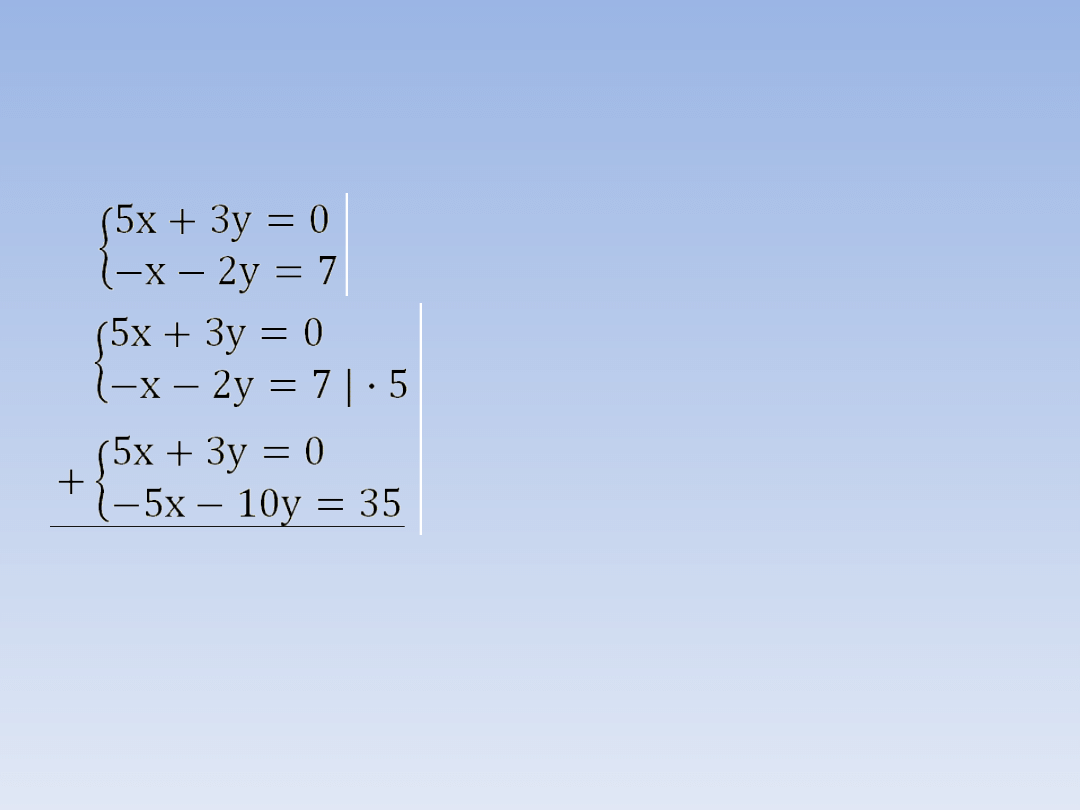
PRZYKŁADY.

PRZYKŁAD 2.

-7y = 35 | :

 

(-7)

y = -5

W tym układzie przy żadnej niewiadomej nie 
występują przeciwne współczynniki, musimy 
więc odpowiednio przekształcić równania.

Obie strony drugiego równania mnożymy 
przez 5, dzięki temu uzyskamy przeciwne 
współczynniki przy x: 5 i -5.

Obie strony równań dodajemy do siebie.

Rozwiązujemy otrzymane równanie z jedną 
niewiadomą (y).

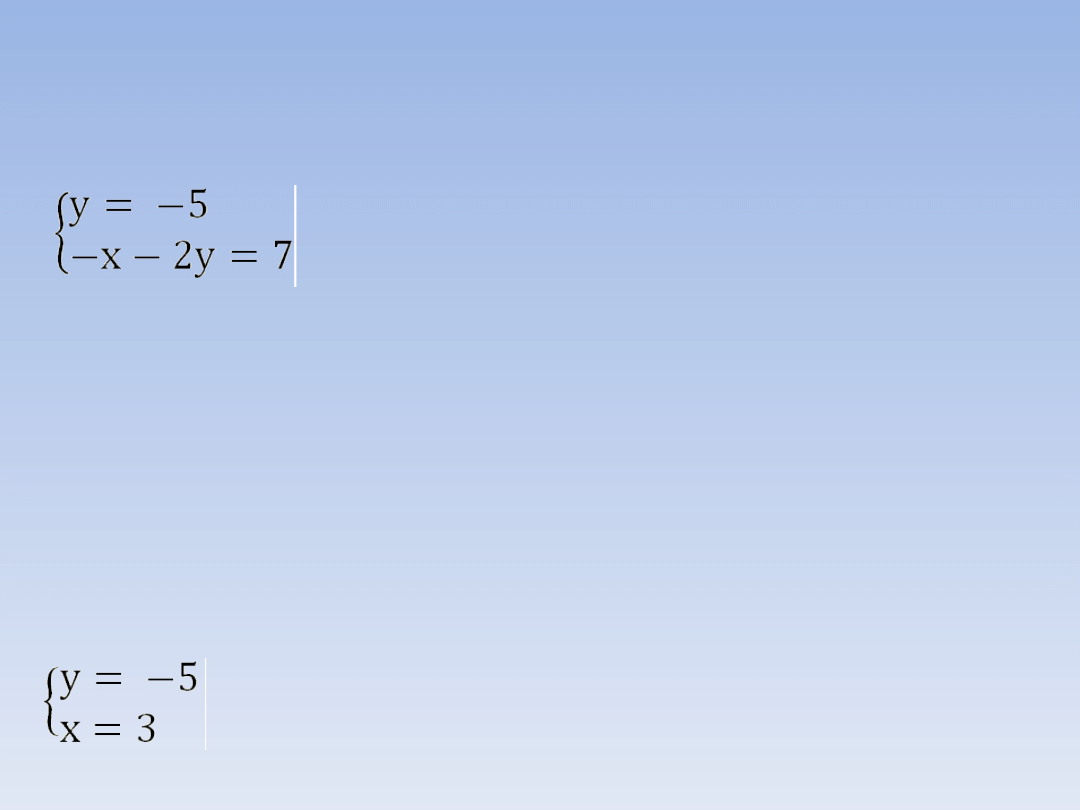
PRZYKŁADY.

PRZYKŁAD 2 – ciąg dalszy.

-x – 2 ∙ (-5) = 7

- x + 10 = 7

- x = -3 | :

 

(-1)

x = 3

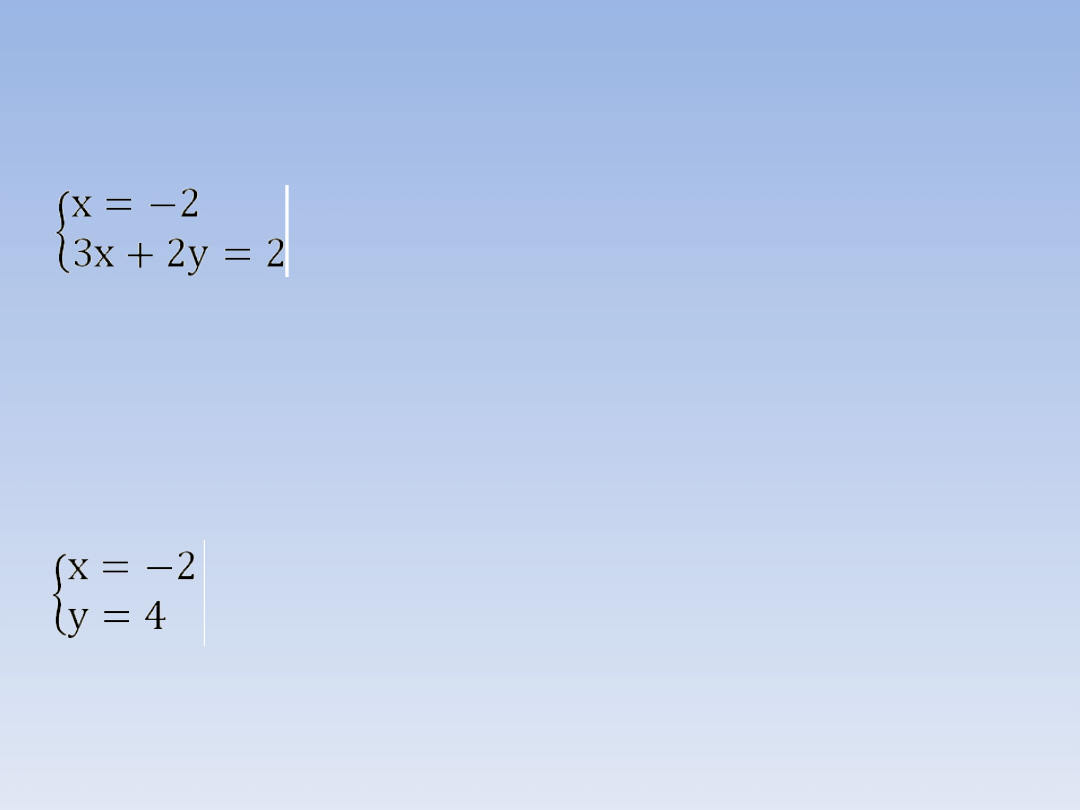
Obliczoną niewiadomą y = -5 wstawiamy do 
jednego (dowolnego) równania układu i obliczamy 
drugą niewiadomą

Rozwiązanie układu równań.

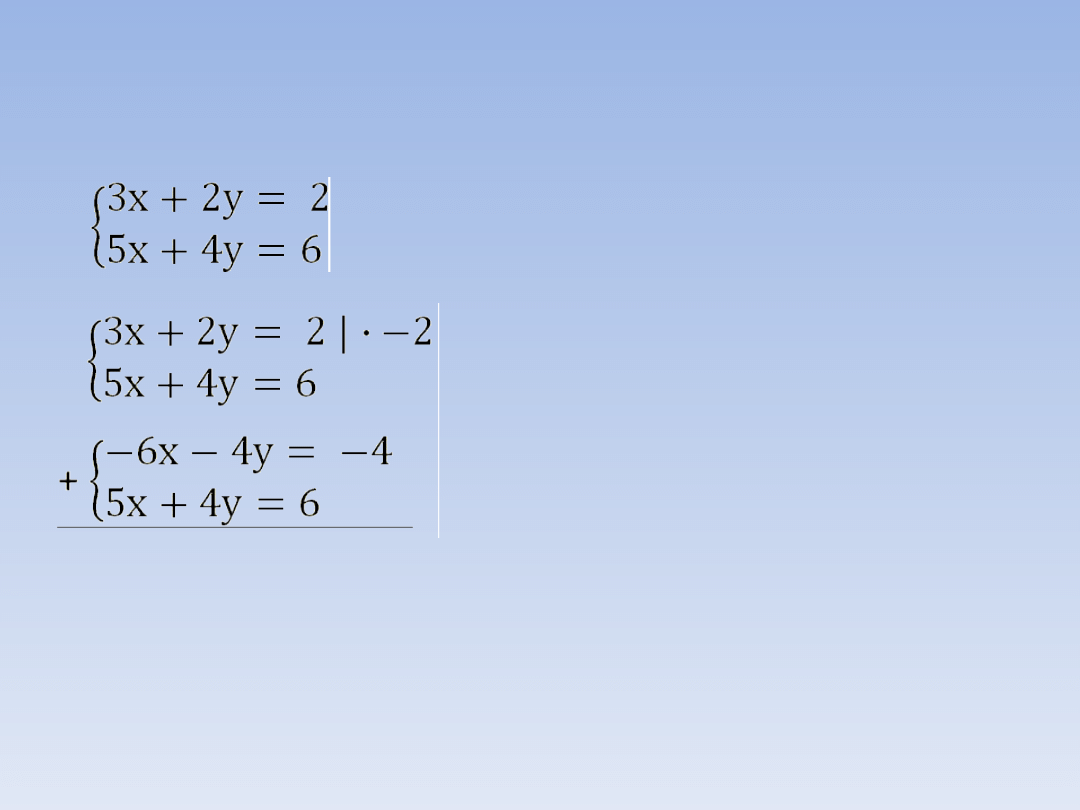
PRZYKŁADY.

PRZYKŁAD 3.

-x = 2 |:

 

(-1)

x = -2

Obie strony pierwszego równania 
mnożymy przez -2, dzięki temu uzyskamy 
przeciwne współczynniki przy y: -4 i 4.

Rozwiązujemy otrzymane równanie z jedną 
niewiadomą x.

W tym układzie także przy żadnej niewiadomej 
nie występują przeciwne współczynniki, 
przekształcamy równania tak, aby je uzyskać.

Obie strony równań dodajemy do siebie.

PRZYKŁADY.

PRZYKŁAD 3 – ciąg dalszy.

3 ∙ (-2) + 2y = 2
-6 + 2y = 2
2y = 8 | :

 

2

y = 4

Obliczoną niewiadomą x = -2 wstawiamy do 
jednego (dowolnego) równania układu i obliczamy 
drugą niewiadomą

Rozwiązanie układu równań.

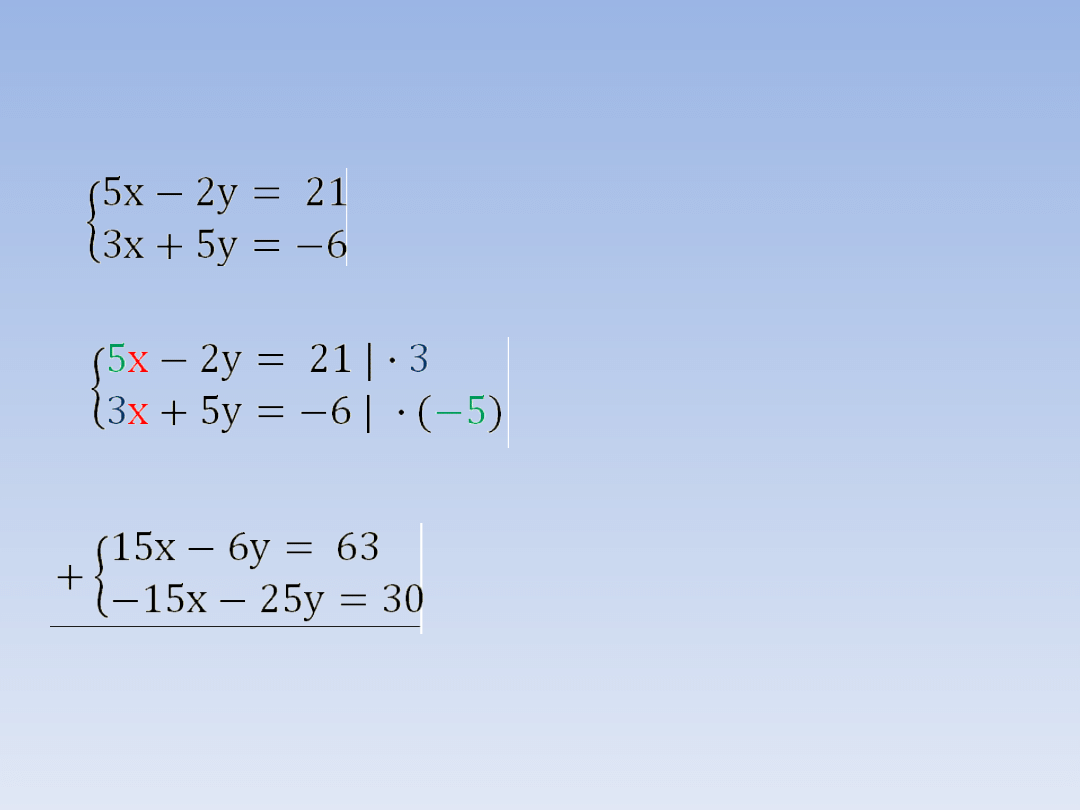
PRZYKŁADY.

PRZYKŁAD 4.

-31y = 93 | :

 

(-31)

y = -3

Aby rozwiązać ten przykład musimy przekształcić 
oba równania. Wybierzmy najpierw niewiadomą, 
przy której chcemy uzyskać przeciwne 
współczynniki. Niech to będzie x.

Dzięki powyższej operacji otrzymaliśmy 
przeciwne współczynniki przy x. 
Dodajemy do siebie obie strony równań 
układu.

Pierwsze równanie mnożymy przez 
współczynnik stojący przy x w 
drugim równaniu: 

3

. Drugie 

równanie mnożymy przez 
współczynnik stojący przy x w 
pierwszym równaniu, ale 
zmieniamy jego znak na 
przeciwny: 

-5

.

PRZYKŁADY.

PRZYKŁAD 4 – ciąg dalszy.
y = -3

5x – 2 ∙ (-3) = 21
5x + 6 = 21 | -

 

6

5x = 15 |:

 

5

x = 3

Obliczoną niewiadomą y = -3 wstawiamy do 
jednego (dowolnego) równania układu i obliczamy 
drugą niewiadomą

Rozwiązanie układu równań.

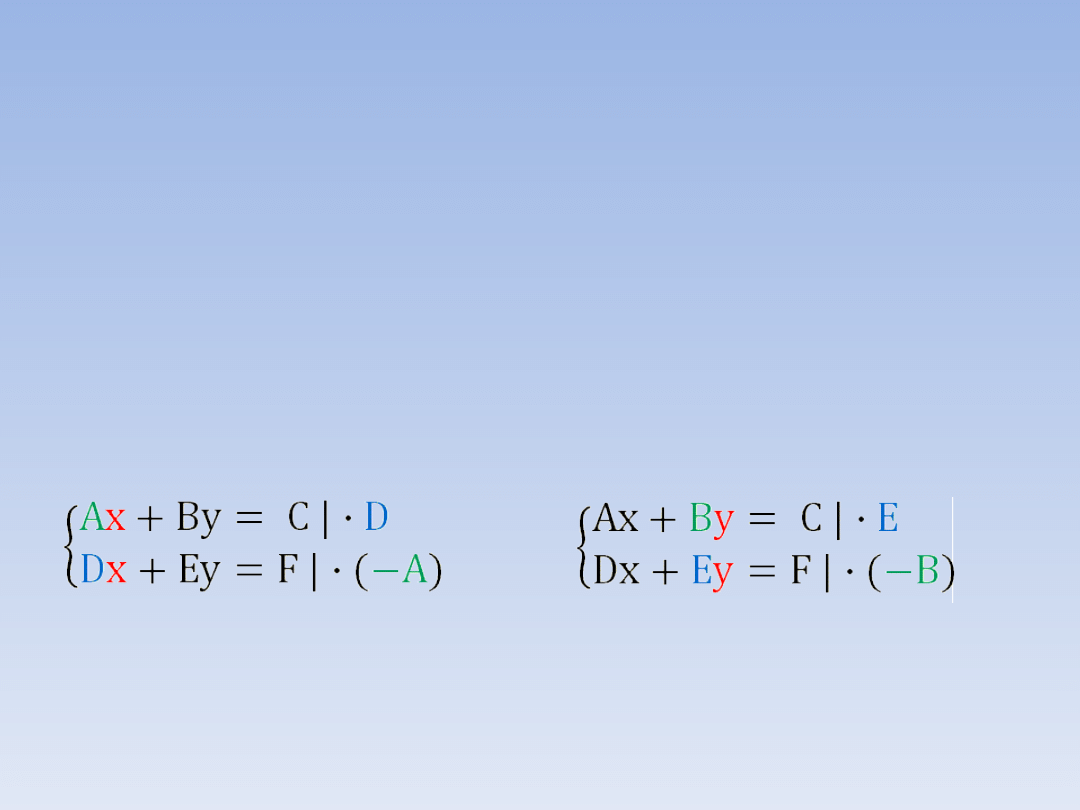
PRZYKŁAD 4.

Metoda  przedstawiona  w  przykładzie  4  jest 
uniwersalna  i  pozwala  uzyskać  przeciwne 
współczynniki  przy  wybranej  niewiadomej  w 
każdym 

układzie 

równań. 

Oczywiście 

pamiętajmy, że nie można mnożyć równania 
przez 0.