dr inż. Grażyna Kałuża

pokój

103

METODY NUMERYCZNE

Gliwice 2010

wykład

konsultacje:

wtorek 10:00-11:30

środa 10:00-11:30

www.kwmimkm.polsl.pl

Program przedmiotu



wykład: 15 godzin w semestrze



laboratorium: 30 godzin w semestrze

Warunki zaliczenia



zaliczenie na ocenę pozytywną laboratorium (L)



zaliczenie na ocenę pozytywną kolokwium z wykładu (W)

Ocena końcowa

O=0.5 W+0.5 L

Gliwice 2010

Literatura podstawowa

Majchrzak E., Mochnacki B.:

Metody numeryczne. Podstawy teoretyczne, aspekty praktyczne i algorytmy,

Wydawnictwo Politechniki Śląskiej, wyd. IV, Gliwice 2004.

Gliwice 2010

Gliwice 2010

Układy równań liniowych

Gliwice 2010

Układy równań liniowych

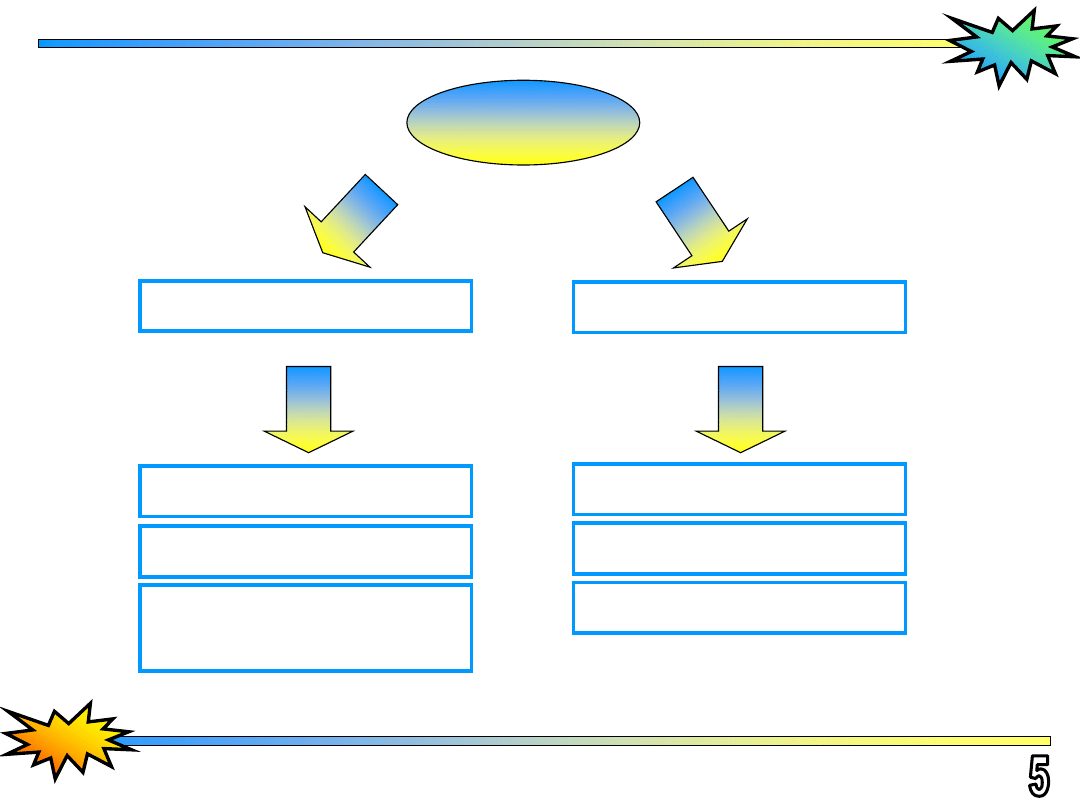
Algorytmy

obliczeniowe

Metody dokładne

Metoda Cramera

Metoda Thomasa

Metoda eliminacji

Gaussa

Metody iteracyjne

Metoda iteracji prostej

Metoda Gaussa-Seidla

Metoda nadrelaksacji

Gliwice 2010

Metody dokładne rozwiązywania

układów równań

Gliwice 2010

Rozpatruje się układ

n

- równań liniowych

zawierających

n

-

niewiadomych

Układy równań liniowych

11 1

12 2

1

1

21 1

22 2

2

2

1 1

2

2

...

...

.............................................

...

n

n

n

n

n

n

n n

n

n

a x

a x

a x

b

a x

a x

a x

b

a x

a x

a x

b



 









 













 





który można zapisać w postaci macierzowej

 

A X

B

Gliwice 2010

Układy równań liniowych

gdzie:

11

12

1

21

22

2

1

2

...

...

...................

...

n

n

n

n

nn

a a

a

a a

a

a a

a



























A

1

2

n

x

x

x

 

 

 



 

 

 

X

1

2

n

b

b

b

 

 

 



 

 

 

B

macierz główna

układu

wektor

niewiadomych

wektor wyrazów

wolnych

Gliwice 2010

Układy równań liniowych

Układ równań posiada jedno rozwiązanie wtedy i tylko wtedy gdy

jest

oznaczony

UWAGA:

macierz

główna

układu

równań

A

nie

jest

osobliwa

(wyznacznik z tej macierzy jest różny od zera)

Gliwice 2010

Zastosowanie macierzy odwrotnej

Gliwice 2010

Przedstawiony powyżej układ równań liniowych zapisany

w postaci macierzowej

Zastosowanie macierzy odwrotnej

 

A X

B

można rozwiązać obliczając macierz odwrotną do

macierzy głównej układu.

1







X

A

B

Jeżeli macierz główna układu równań nie jest osobliwa

to wektor niewiadomych oblicza się z zależności:

Gliwice 2010

Trójkątne układy równań liniowych

Gliwice 2010

Trójkątny układ równań

Jeżeli układ równań ma następującą postać

11 1

1 2

2

1

1

2 2

2

2

2

...

...

..........................

n

n

n

n

n n

n

n

a x

a x

a x

b

a x

a x

b

a x

b



 







 















trójkątny układ równań

Gliwice 2010

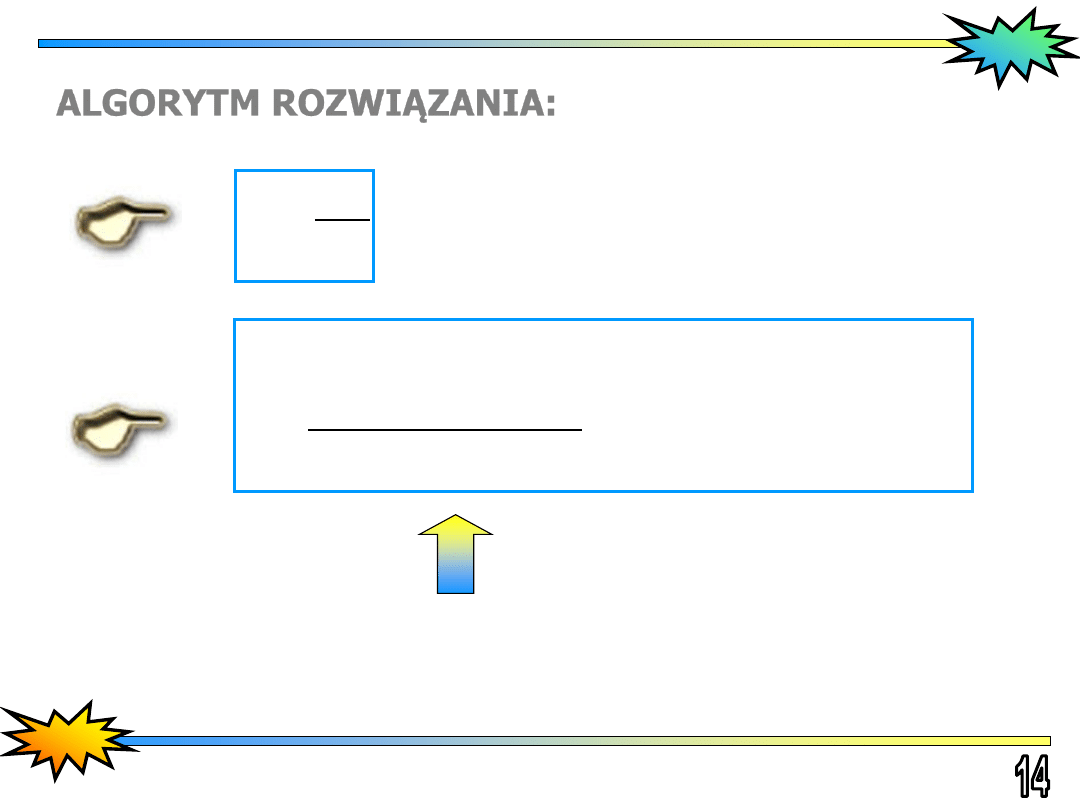
ALGORYTM ROZWIĄZANIA:

Trójkątny układ równań

n

n

n n

b

x

a







1

,

1 ,

2, ... , 1

n

i

i s

s

s

i

i

i i

b

a

x

x

i

n

n

a

 







 





Zakładamy, że

0 ,

1, 2, ... ,

i i

a

i

n





Gliwice 2010

Metoda Thomasa dla układów

trójprzekątniowych

Gliwice 2010

Metoda Thomasa

Algorytm

Thomasa

bywa

nazywany

w

literaturze

metodą progonki

(przeganiania).

Rozpatrujemy liniowy, trójprzekątniowy układ równań

1

1

1

1

2

2

2

2

2

3

3

3

3

3

1

1

1

1

1

.

.

.

.

.

n

n

n

n

n

n

n

n

n

b

c

x

d

a

b

c

x

d

a

b

c

x

d

a

b

c

x

d

a

b

x

d













 

 





 

 





 

 





 

 









 

 





 

 





 

 





 

 





 

 



Gliwice 2010

Metoda Thomasa

który można zapisać również w następujący sposób

1

1

1

,

1, 2,

0

... ,

,

,

0

n

i

i

i

i

i

i

i

a x

b x

c x

d

i

n

a

c

















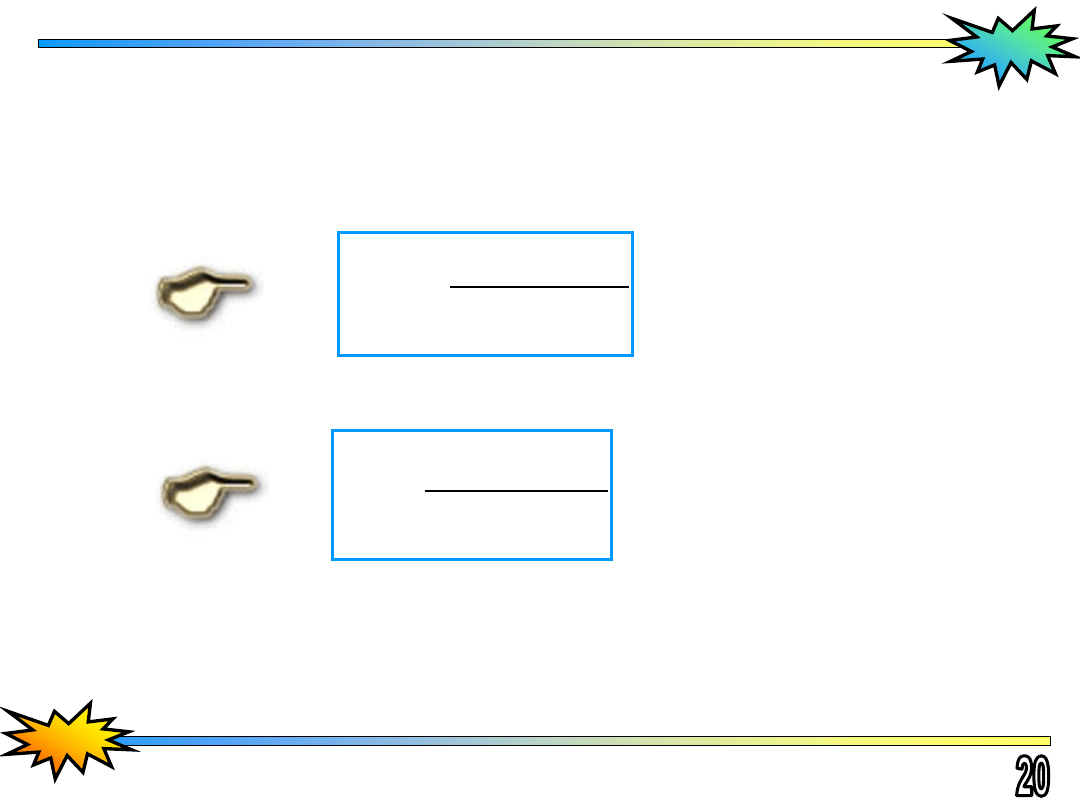
Rozwiązania tego układu równań poszukuje się w postaci

1

β

γ

i

i

i

i

x

x







(1)

(2)

lub inaczej zapisując

1

1

1

β

γ

i

i

i

i

x

x











gdzie i są nieznanymi współczynnikami.

β

i

γ

i

Gliwice 2010

Metoda Thomasa

Po podstawieniu

(2)

do

(1)

i uporządkowaniu otrzymujemy:

1

β

β

i

i

i

i

i

c

a

b



 



1

1

γ

γ

β

i

i

i

i

i

i

i

d

a

a

b











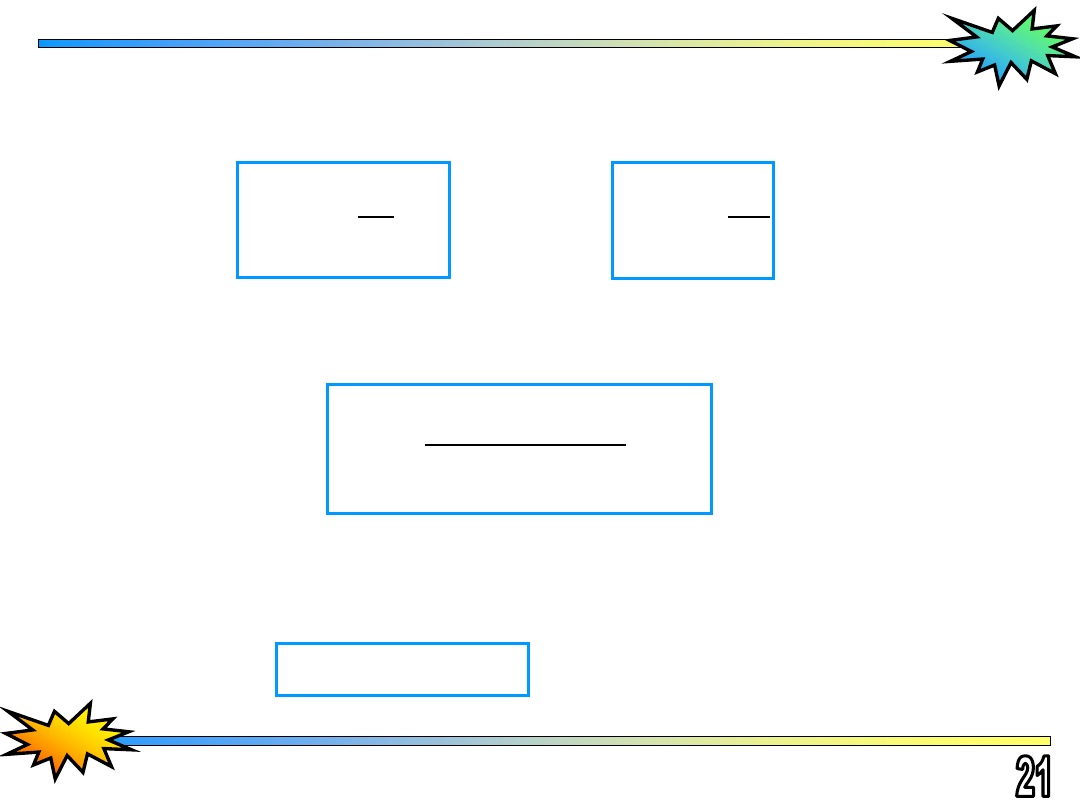
Gliwice 2010

Metoda Thomasa

Z danych przedstawionych w równaniu

(1)

można wyznaczyć

wartości początkowe (dla

i = 1

)

1

1

1

β

,

c

b

 

1

1

1

γ

d

b



oraz wartość ostatniej niewiadomej (dla

i = n

)

1

1

γ

γ

β

n

n

n

n

n

n

n

n

d

a

x

a

b













Po wyznaczeniu wartości

kolejne niewiadome obliczamy

z równania

n

x

1

β

γ

i

i

i

i

x

x







dla

i = n



1, n



2, ... , 1

Gliwice 2010

Metoda eliminacji Gaussa

Gliwice 2010

Metoda eliminacji Gaussa

Układ równań

liniowych

11

12

1

21

22

2

1

2

...

...

...................

...

n

n

n

n

n n

a a

a

a

a

a

a

a

a































A

1

2

n

b

b

b

 

 

 



 

 

 

B

11 1

12 2

1

1

21 1

22 2

2

2

1 1

2

2

...

...

.............................................

...

n

n

n

n

n

n

n n

n

n

a x

a x

a x

b

a x

a x

a x

b

a x

a x

a x

b



 









 













 





Macierz główną układu równań i wektor wyrazów wolnych:

zapisujemy w postaci macierzy

C

, w której macierz główną

A

uzupełnia się dodatkową kolumną zawierającą wektor wyrazów
wolnych

B.

Gliwice 2010

Metoda eliminacji Gaussa

11

12

1

1,

1

21

22

2

2,

1

1

2

,

1

n

n

n

n

n

n

nn

n n

c

c

c

c

c

c

c

c

c

c

c

c

















































C

i j

a

i

b

i j

a

i

b

n

- pierwszych kolumn stanowią elementy

n

+ 1 - kolumnę stanowią elementy

Gliwice 2010

Metoda eliminacji Gaussa

Podstawowy wariant metody eliminacji Gaussa:

Pierwszy etap

Przekształcenie

macierzy

C

w

taki

sposób,

aby

n

pierwszych kolumn tworzyło macierz trójkątną

Drugi etap

Rozwiązanie trójkątnego układu równań

Gliwice 2010

Metoda eliminacji Gaussa

Jeżeli

11

0

c



Pierwsze równanie mnożymy przez:

1

11

i

c

c

Odejmujemy to równanie od każdego kolejnego

i

- tego

równania (

i = 2, 3, …, n

)

Obliczone współczynniki zapisujemy na miejscu poprzednich.

Pierwszy etap

Krok 1

Gliwice 2010

Otrzymujemy następujący układ równań

Metoda eliminacji Gaussa

11 1

12

2

13 3

1

1,

1

(1)

(1)

(1)

(1)

22

2

23

3

2

2,

1

(1)

(1)

(1)

(1)

32

2

33

3

3

3,

1

(1)

(1)

(1)

2

2

3

3

,

...

...

...

...................................................

...

n

n

n

n

n

n

n

n

n

n

n

n n

n

n n

c x

c x

c x

c x

c

c x

c x

c x

c

c x

c x

c x

c

c x

c x

c x

c











 





 





 





 



(1)

1





















Gliwice 2010

Układ ten odpowiada sprowadzeniu macierzy

C

do

C

1

Metoda eliminacji Gaussa

11

12

13

1

1,

1

(1)

(1)

(1)

(1)

22

23

2

2,

1

(1)

(1)

(1)

(1)

32

33

3

3,

1

1

(1)

(1)

(1)

(1)

2

3

,

1

0

0

0

n

n

n

n

n

n

n

n

n n

n n

c

c

c

c

c

c

c

c

c

c

c

c

c

c

c

c

c































































C

za pomocą wzorów określających nowe współczynniki

1

(1)

1

1 1

i

i j

i j

j

c

c

c

c

c





2, 3, ... ,

i

n



2, 3, ... ,

1

j

n





dla

Gliwice 2010

Metoda eliminacji Gaussa

Jeżeli

(1)

22

0

c



Drugie równanie mnożymy przez:

(1)

2

(1)

22

i

c

c

Odejmujemy to równanie od każdego kolejnego

i

- tego

równania (

i = 3, 4, …, n

)

Obliczone współczynniki zapisujemy na miejscu poprzednich.

Krok 2

Gliwice 2010

Otrzymujemy następujący układ równań

Metoda eliminacji Gaussa

11 1

12

2

13 3

1

1,

1

(1)

(1)

(1)

(1)

22

2

23

3

2

2,

1

(2)

(2)

(2)

33

3

3

3,

1

(2)

(2)

(2)

3

3

,

1

...

...

...

........................................

...

n

n

n

n

n

n

n

n

n

n

n n

n

n n

c x

c x

c x

c x

c

c x

c x

c x

c

c x

c x

c

c x

c x

c













 









 







 











 





Gliwice 2010

Układ ten odpowiada sprowadzeniu macierzy

C

1

do

C

2

Metoda eliminacji Gaussa

za pomocą wzorów określających nowe współczynniki

11

12

13

1

1,

1

(1)

(1)

(1)

(1)

22

23

2

2,

1

(2)

(2)

(2)

33

3

3,

1

2

(2)

(2)

(2)

3

,

1

0

0

0

0

0

n

n

n

n

n

n

n

n n

n n

c

c

c

c

c

c

c

c

c

c

c

c

c

c

c































































C

3, 4, ... ,

i

n



3, 4, ... ,

1

j

n





dla

(1)

2

(2)

(1)

(1)

2

(1)

2 2

i

i j

i j

j

c

c

c

c

c





Gliwice 2010

Metoda eliminacji Gaussa

Kontynuując takie postępowanie, po wykonaniu

n

kroków

dochodzimy do

trójkątnego układu równań

11 1

12

2

13 3

1

1,

1

(1)

(1)

(1)

(1)

22

2

23

3

2

2,

1

(2)

(2)

(2)

33

3

3

3,

1

(

1)

(

1)

,

1

...

...

...

.......................................

n

n

n

n

n

n

n

n

n

n

n

n n

n

n n

c x

c x

c x

c x

c

c x

c x

c x

c

c x

c x

c

c

x

c

















 









 







 















Gliwice 2010

Metoda eliminacji Gaussa

któremu odpowiada przekształcona macierz

C

n



1

11

12

13

1

1,

1

(1)

(1)

(1)

(1)

22

23

2

2,

1

(2)

(2)

(2)

33

3

3,

1

1

(

1)

(

1)

,

1

0

0

0

0

0

0

n

n

n

n

n

n

n

n

n

n n

n n

c

c

c

c

c

c

c

c

c

c

c

c

c

c





































































C

Gliwice 2010

Metoda eliminacji Gaussa

Przejście od układu równań liniowych do układu trójkątnego

realizowane jest za pomocą następującego ciągu wzorów

(

1)

( )

(

1)

(

1)

(

1)

1 , 2 , ... ,

1

1 ,

2 , ... ,

,

1,

2, ... ,

1

s

i s

s

s

s

i j

i j

s j

s

s s

s

n

i

s

s

n

c

c

c

c

j

s

s

n

c















  



















 







 



Gliwice 2010