IV. 13. Metody numeryczne rozwiązywania układów liniowych równań algebraicznych.

1. Metody bezpośrednie:

• oznaczenia :

E₁ a₁₁x₁ + a₁₂x₂ +...+ a_1nx_n = b₁

E₂ a₂₁x₁ + a₂₂x₂ +...+ a_2nx_n = b₂

_* Ax = b

E₁ a₃₁x₁ + a₃₂x₂ +...+ a_3nx_n = b₃

rozwiązanie jest jednoznaczne gdy:

b ≠ 0 i det(A) ≠ 0

1. Gaussa (eliminacji) - polega na sprowadzeniu równania Ax = b

do postaci górnotrójkątnej Ux = (b)^<n>

U - macierz otrzymana w wyniku wykonania n operacji elementarnych na macierzy A

(b)^<n> - wektor otrzymany w wyniku wykonania n operacji elementarnych ba

Def. Operacja elementarna nie zmienia wyniku równania np:

λE_i → E_i λ ≠ 0

E_i +λE_j → E_i

E_i ,E_j -wiersze równania.

Postępowanie wprzód

krok 1

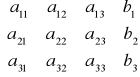
krok 2 działanie

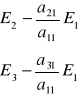
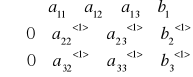
krok 3 działanie

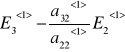
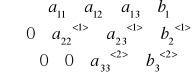
koniec postępowania wprzód.

Postępowanie wstecz:

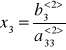
itd...

jeśli na przekątnej macierzy A znajduje się 0 to procedura zostaje przerwana.

Def. Macierz A nazywamy macierzą z silnie dominującą przekątną główną jeśli

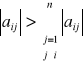
Def. Macierz A nazywamy dodatnio określoną jeśli forma kwadratowa

x^TAx > 0 dla dowolnego x=0

Tw. Gdy macierz A ma silnie dominującą przekątną główną jest nieosobliwa. Jest to warunek wystarczający.

Ponadto rozwiązanie równania Ax =b można otrzymać metodą Gaussa bez zmiany kolejnści wierszy i kolumn i rozwiązanie jest silnie stabilne ze wzgl edu na wzrost błędu zaokrąglenia.

Tw. Gdy macierz A jest dodatnio określona to jest nieosobliwa. Jest to warunek wystarczający. Ponadto rozwiązanie równania Ax =b można otrzymać metodą Gaussa bez zmiany kolejnści wierszy i kolumn i rozwiązanie jest silnie stabilne ze wzgl edu na wzrost błędu zaokrąglenia.

Tw. Silwestra. Macierz A jest dodatnio określona jeśli ma wszystkie wartości wlasne WKW

1.2. Metoda Gaussa z częściowym wyborem elementu wiodącego.

k

m szukamy p elementu wiodącego

k z warunku :

a_pk = maxa_ik

0_ ... p i = k....m

przestawiamy E_p na miejsce E_k ( należy notować liczbę

przestawień)

1.3. Metoda Gaussa z pełnym wyborem elementu wiodącego.

a_pi = maxa_ij

i,j = k....m

1.4. Metoda Gaussa z częściowym wyborem elementu wiodącego i skalowaniem.

Definicja współczynnika s_i dla każdego wiersza s_i = maxa_ij

j = 1...m

dla otrzymania zer w pierwszej kolumnie ustalamy numer k równania z warunku

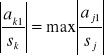
i dokonujemy zamiany E₁ na E_k

j = 1...n

1.2. Metoda Dolittle'a l_ii = 1

Crouta u_ii = 1

Choleskiego u_ii = l_ii

Ax =b

A = LU L - mac. dolnotrójkątna U - mac. górnotrójkątna

LUx =b

Lc =b otrzymujemy c

Ux =c otrzymujemy x

wyznaczenie L i U

dane

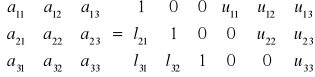
po wymnożeniu macierzy L i U

u₁₁ = a₁₁

u₁₂ = a₁₂

u₁₃ = a₁₃ itd...

Dla macierzy symetrycznej i dodatnio określonej rozklad trójkątny upraszcza się do postaci

A = LL^T

W metodzie Choleskiego dla uniknięcia pierwiastkowania korzystniejszy jest rozkład

A = LDL^T L - macierz trójkątna z jedynkami na przekątnej

D - macierz diagonalna

Ax =b

LDL^Tx =b

DL^Tx = c

Lc =b otrzymujemyc

Dd =c otrzymujemyd

L^Tx =d otrzymujemyx

1.6. Metoda Gaussa - Jordana.

Ax =b

A^-1Ax =b

x = A^-1b

wyznaczenie macierzy A^-1 -postępowanie podobnie jak w metodzie Gaussa.

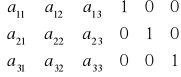
2.1. Układy równań podokreślone.

A-macierz o wymiarze m*n gdzie m < n

metoda Gaussa - Jordana

Ix₁ -Ax₂ =b

2.2. Układy nadokreślone.

3. Metody iteracyjne - polegają na przyjeciu wektora startowego x⁰ oraz generowanie ciągu wektorów x^k zbieżnych do rozwiązania x.

3.1. Metoda Jacobiego.

Ax =b

A = D - L - U

x^<k> = T(x )^<k-1>+c

(D-L-U)x =b

D(x)^<k> = (L-U) (x)^<k-1>+b

Zakończenie iteracji gdy norma względna

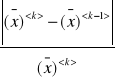
dąży do zera.

3.2. Metoda Gaussa - Seidela

(D-L-U)x =b

(x)^<k> = (D-L)^-1U (x)^<k-1>+(D-L)^-1b

Warunkiem wystarczającym by proces był zbieżny dla dowolnego x⁰ jest aby mac. A miała silnie dominującą przekątną główną.

3.3. Metoda relaksacyjna

Def. Wektor reziduum r =b - Ax

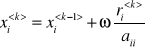
ω - wsp. relaksacji gdy 0< ω<1 - podrelaksacja

ω>1 - nadrelaksacja

IV. 14. Metody aproksymacji funkcji jednej zmiennej.

Aproksymację stosujemy gdy :

1. złożoną funkcję chcemy przedstawić w prostej postaci.

2. funkcja dana jest w postaci tablicy

3. funkcja jest nieznana ( poszukiwanie równań różniczkowych )

Ogólnie - przedstawiamy funkcję w postaci kombinacji liniowej pewnych danych funkcji bazowych.

φ(x) = a₀u₀(x) + a₁u₁(x) + ... + a_nu_n(x) ≈ f(x)

B_(x) = [ u₀(x), u₁(x), ..., u_n(x) ] - macierz funkcji bazowych ( liniowo niezależne)

a^T = [ a₀, a₁, ... , a_n ] - wektor nieznanych współczynników

φ(x) = B_(x)a

1.Aproksymacja punktowa.

- Funkcja f(x) dana jest w postaci tablicy x_= [x₀, x₁, ... , x_n ] i odpowiadających wartości F = [f₀, f₁, ... , f_n ].

-Należy dobrać współczynniki a_i i=0,1...n tak aby

możliwie najlepiej przybliżał F(x) , ( baza B_(x) ułożona z jednomianów )

-Należy rostrzygnąć stopień wielomianu i kryterium jakości aproksymacji, najczęściej stosuje się kryterium najmniejszych kwadratów.

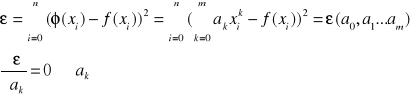
Dla przypadku wielomianu uogólnionego:

φ(x) = a₀u₀(x) + a₁u₁(x) + ... + a_mu_m(x) powstaje układ równań o postaci :

w zapisie macierzowym:

U^TUa = U^TF

gdzie:

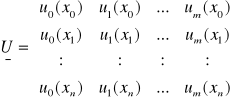
Równania znacznie się upraszczają gdy funkcje u_k(x) są ortogonalne

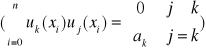
wtedy U^TU przyjmie postać:

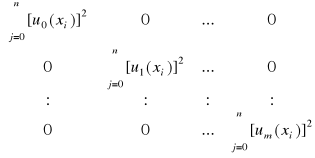
np.: funkcje Czebyszewa,

2. Aproksymacja calkowa.

Funkcja f(x) jest określona i ciągla w przedziale [a,b]

metoda najmniejszych kwadratów

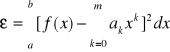
np.: dla m = 2

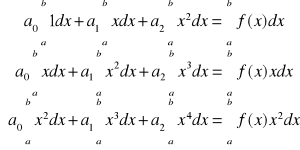
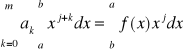
3. Aproksymacja funkcjami ortogonalnymi.

Def. Funkcja wagowa - taka funkcja w(x) , że w(x) ≥ 0 , w [a,b] , lub w(x)≠0 w pewnym przedziale [a,b], np.:

w∈[-1,1]

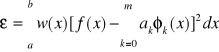
- błąd średni kwadratowy z wagą w .

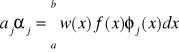
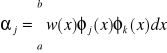
1) 0 j≠k

2) α_j > 0 j=k - funkcja ortogonalna z wagą

3) α_j = 1 j=k - funkcja ortogonalna

Wielomiany Legendra w(x)1 w [-1,1] - ortogonalne

Funkcja Czebyszewa

w [-1,1] - ortogonalne

Jeśli f(x) jest aproksymowalne w [a,b] to dokonujemy przekształcenia na przedział [-1,1] według wz:

t ∈ [-1,1]

IV. 15. Metody numeryczne rozwiązywania równań nieliniowych.

1)Dobór algorytmu gwarantującego zbieżność iteracji.

2)Dobór punktu startowego.

1. Metoda bisekcji polega na systematycznym okrojeniu przedziału w którym istnieje pierwiastek.

f(x) ∈ (a,b) f(a)f(b) < 0

gdy : f(a₁)f(ρ₁) > 0 to a₂ = ρ₁ b₂ = b₁

f(a₁)f(ρ₁) < 0 to a₂ = a₁ b₂ =ρ₁

warunek zakończenia iteracji ρ_n - ρ_n-1 < ε₁ i f( ρ_n ) < ε₂

2. Metoda punktu stałego.

Def. Punktem stałym przekształcenia g nazywamy pierwiastek x = ρ , g(x) = x , f(x) = 0

Przykład :

e^x = x+2 e^x-2=x g(x)=e^x-2

ρ_n+1 = g(ρ_n)

ρ_n+1 = e^ρ_n - 2

3. Metoda stycznych Newtona - Raphsona.

zał: f(x) ∈ C² w (a,b) x ∈ [a,b] i jest przybliżeniem pierwiastka takim że,

f `(x ) ≠0 , x -p - małe

f(x)=f(x +( x-x ))=f(x )+f `(x )(x-x)+ ...

gdy : x=p to f(p)≡0 ≈ f(x )+f `(x )(p-x )

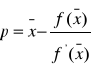
Wzór iteracyjny

n=1,2...

4. Metoda siecznych.

wzór iteracyjny:

wadą jest to, że muszą być dwa punkty startowe.

5. Metoda Reguła-Falsi

- zmodyfikowana metoda siecznych tak aby w procesie iteracji pierwiastek był zawsze zawarty w przedziale [a_i ,b_i] , f(a_i )f(b_i ) < 0

lub:

a_n=a_n-1 ; b_n = p_n gdy f(a_n-1)f(p_n) < 0

a_n=p_n ; b_n = b_n-1 gdy f(a_n-1)f(p_n) > 0

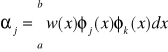
1 0_

1

1

1

0_ 1

G_

1 0_

1

1

0_ 1

---