„Matematyka to pismo 

wyryte w ludzkiej 

świadomości przez samego 

Ducha Życia.”

Claude Fayette Bragdon

ROZWIĄZYWANIE UKŁADÓW 

RÓWNAŃ – METODA 

GRAFICZNA.

We  wszystkich  naszych  lekcjach  dotyczących 
układów  równań  mowa  jest  ciągle  o 
równaniach  stopnia  pierwszego  z  dwiema 
niewiadomymi,  czyli  o  równaniach  liniowych. 
Nazwa  „równanie  liniowe”  bierze  się  stąd,  że 
obrazem  takiego  równania  na  płaszczyźnie 
jest  linia  prosta.  Skoro  potrafimy  narysować 
równanie  z  dwiema  niewiadomymi,  możemy 
graficznie rozwiązywać układy równań. 

METODA GRAFICZNA.

Aby  rozwiązać  układ  równań  metodą 
graficzną, 

należy 

każde 

z 

równań 

przedstawić  w  postaci  y  =  ax  +  b  (a,  b  – 
dowolne  liczby;  x,  y  –  niewiadome), 
następnie narysować wykres tych zależności 
w 

jednym 

układzie 

współrzędnych. 

Współrzędne 

punktu 

przecięcia 

się 

wykresów są rozwiązaniem układu równań.

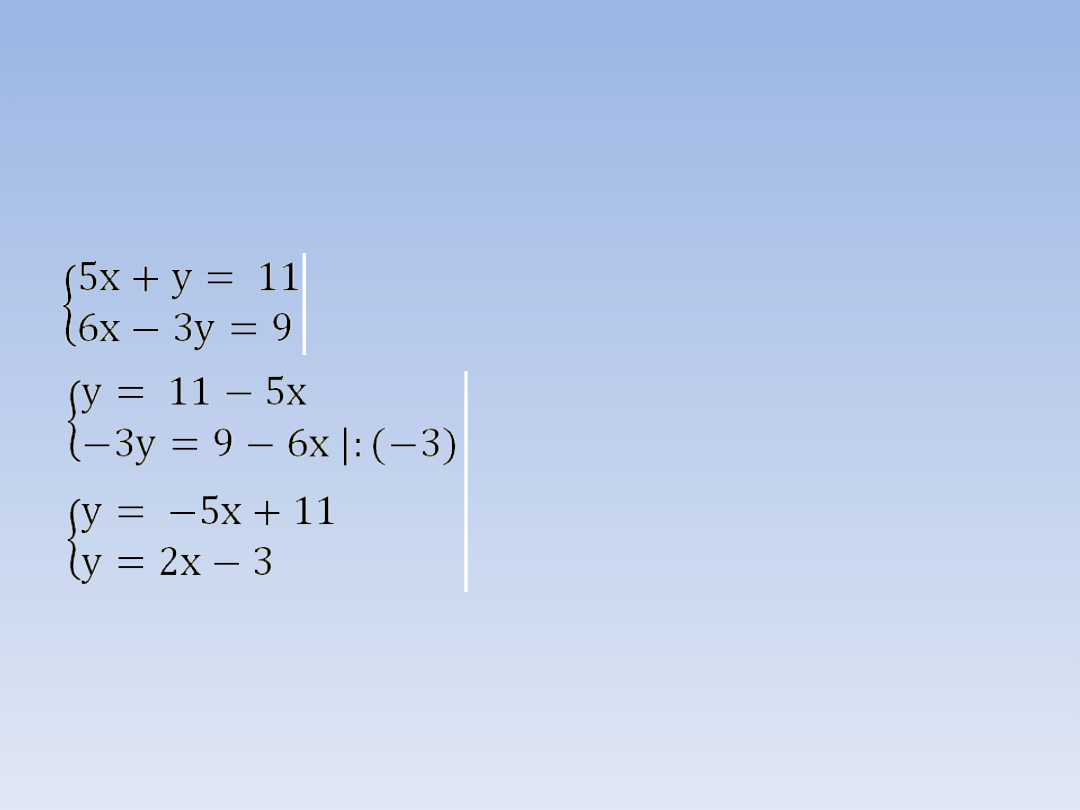
PRZYKŁADY.

PRZYKŁAD 1.
Rozwiąż graficznie układ równań:

Aby  narysować  wykresy  przedstawiające 
równania musimy dla każdego z nich znaleźć 
co najmniej 2 punkty przez które przechodzi 
wykres.

Przekształcamy oba równania do 
postaci 
y = ax +b.

PRZYKŁADY.

PRZYKŁAD 1 – ciąg dalszy.

y = -5x + 11

Wybieram dowolną liczbę (najlepiej taką, aby łatwo 
było zaznaczyć punkt w układzie współrzędnych i 
wykonać obliczenia) i wstawiam do równania w 
miejsce x, następnie obliczam y. Dostaję w ten 
sposób punkt o współrzędnych (x; y).

x = 2
y = -5 ∙ 2 + 11 = -10 + 11 = -1
(2, -1)

x = 3
y = -5 ∙ 3 + 11 = -15 + 11 = -4
(3; -4)

Obliczenie współrzędnych 
pierwszego punktu.

Obliczenie współrzędnych 
drugiego punktu.

PRZYKŁADY.

PRZYKŁAD 1 – ciąg dalszy.

y = 2x – 3

x = 0
y = 2∙ 0 – 3 = 0 – 3 = -3
(0; -3)

x = 1
y = 2 ∙ 1 – 3 = 2 – 3 = -1
(1; -1)

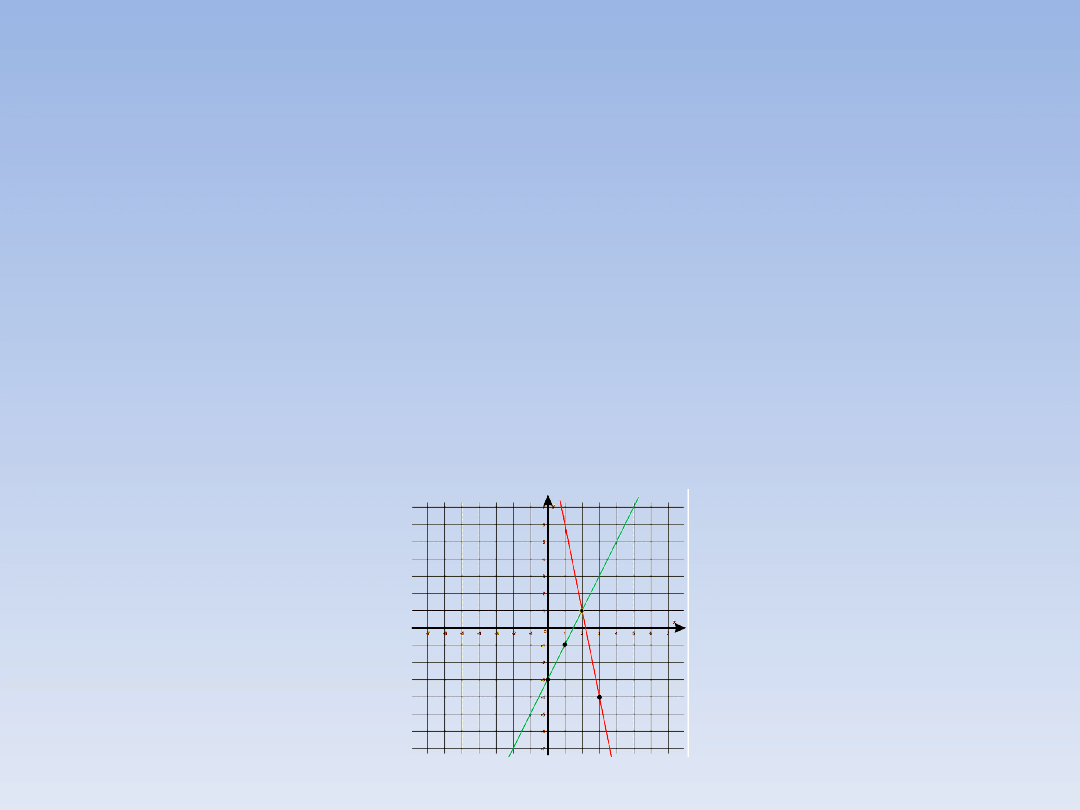
Zaznaczamy 

punkty 

w 

układzie 

współrzędnych 

i 

rysujemy 

wykresy. 

Współrzędne  punktu  w  którym  linie  się 
przecinają są rozwiązaniem układu równań.

PRZYKŁADY.

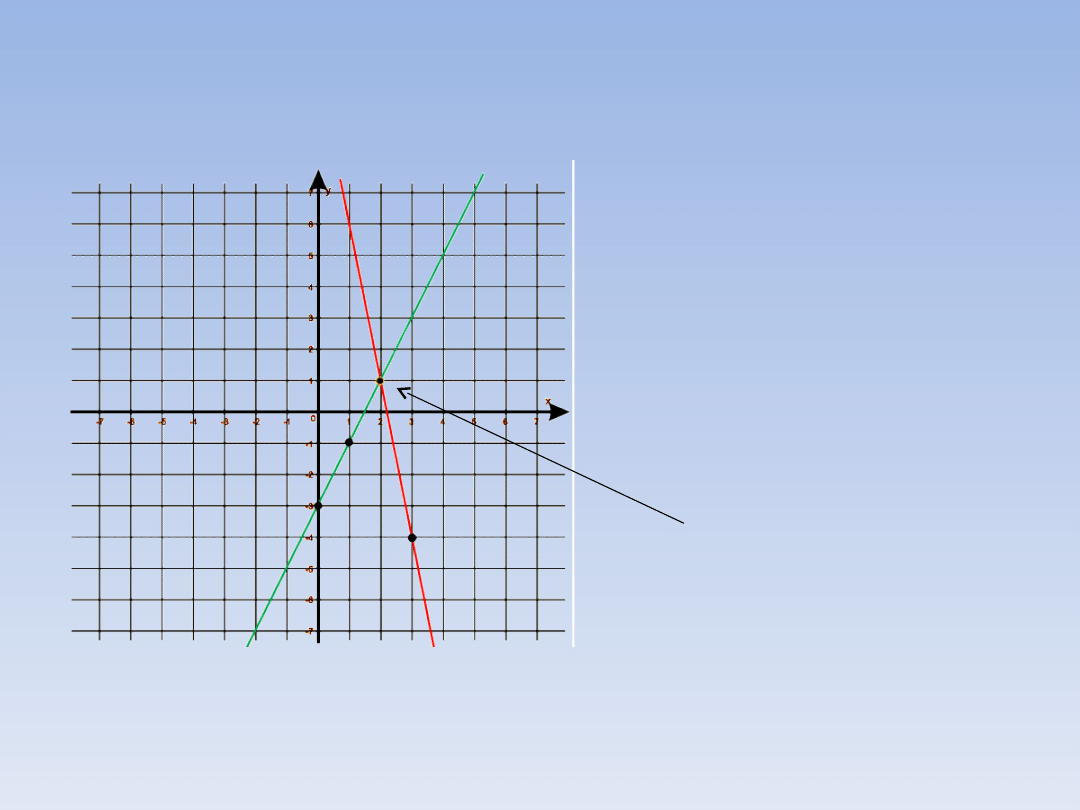
PRZYKŁAD 1 – ciąg dalszy.

Linie  przecinają  się  w 
punkcie 
(2;1),  a  więc  rozwiązaniem 
układu  równań  jest  para 
liczb:
x = 2,
y = 1.

y = -5x + 
11

y = 2x – 3

Rozwiązanie

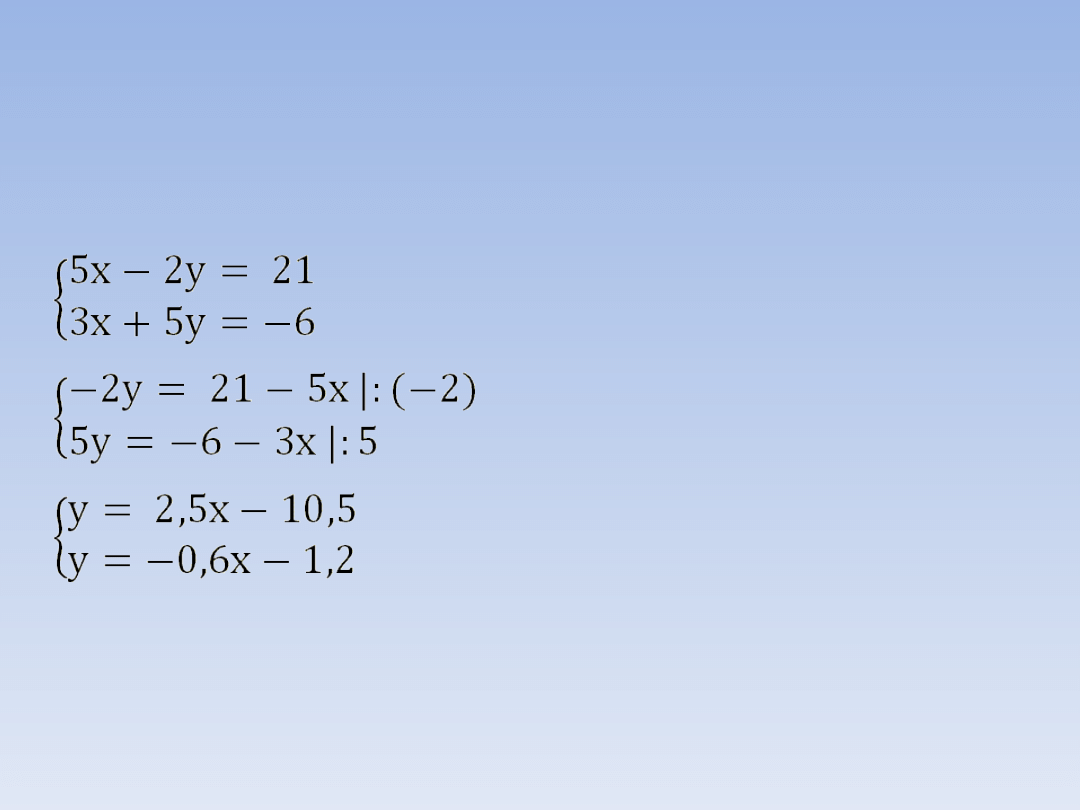
PRZYKŁADY.

PRZYKŁAD 2.
Rozwiąż  poniższy  układ  równań  metodą 

graficzną.

Przekształcamy oba równania do 
postaci 
y = ax +b.

PRZYKŁADY.

PRZYKŁAD 2 – ciąg dalszy.

y = 2,5x – 10,5

x = 3
y = 2,5 ∙ 3 – 10,5 = 7,5 – 10,5 = -3
(3; -3)

x  = 5
y = 2,5 ∙ 5 – 10,5 = 12,5 – 10,5 = 2
(5; 2)

PRZYKŁADY.

PRZYKŁAD 2 – ciąg dalszy.

y = -0,6x – 1,2

x = -2
y = -0,6 ∙ (-2) – 1,2 = 1,2 – 1,2 = 0
(-2; 0)

x = 3
y = -0,6 ∙ 3 – 1,2 = -1,8 – 1,2 = -3
(3; -3)

PRZYKŁADY.

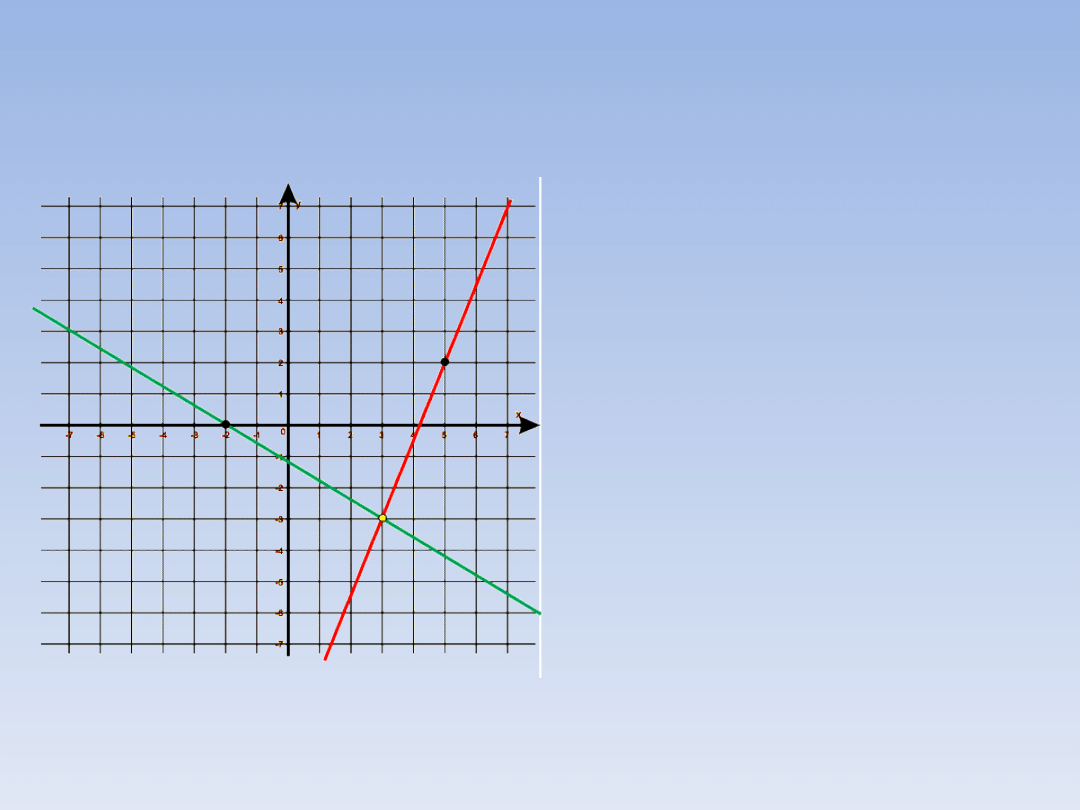
PRZYKŁAD 2 – ciąg dalszy.

Linie  przecinają  się  w  punkcie 
(3;-3), a więc rozwiązaniem układu 
równań jest para liczb:
x = 3,
y = -3.

UWAGA.

Graficzna  metoda  rozwiązywania  układów 
równań  jest  niedokładna.  Wykresy  przez 
nas  sporządzane  zawszę  zawierają  pewne 
błędy,  wynikające  chociażby  z  grubości 
stosowanych  przyborów  do  pisania.  Nie 
zawszę jesteśmy w stanie dokładnie odczytać 
współrzędne  punktu  przecięcia  się  linii, 
zwłaszcza kiedy rozwiązaniem układu równań 
są ułamki. 
Aby  upewnić  się,  czy  odczytane  liczby  są 
rozwiązaniem 

układu 

równań, 

należy 

sprawdzić,  czy  spełniają  oba  równania 
(należy  podstawić  je  do  równań  i  sprawdzić, 
czy otrzymujemy równości prawdziwe).