PODZIAŁ PŁYNÓW

Płyny - w odróżnieniu od ciał stałych zmieniają swój kształt pod działaniem dostatecznie małych sił mechanicznych

- ciecze ρ=const

- gazy ρ = var

kryterium - zmiana objętości

ciecze - płyny zachowujące niemal stałą objętość pod działaniem bardzo wielkich sił mechanicznych i przy dostatecznie małych zmianach temperatury

gazy - płyny znacznie zmieniające swą objętość pod wpływem ciśnienia i temperatury

Różnice termodynamiczne ciecz i gaz 

	ciecz	gaz
gęstość	ρ=const	ρ=p/RT gaz doskonały
Energia wewnętrzna	e = const	e~T
Wykładnik izentropy	k=∞	k= const (1.3, 1.44)
Powierzchnia swobodna	Tak	Nie

CIĄGŁOŚĆ PŁYNU

W mechanice płynów podobnie jak w teorii sprężystości i plastyczności ciał stałych płyn rzeczywisty zastępuje się modelem płynu uproszczonym przez wyeliminowanie struktury cząsteczkowej i nieuporządkowanego ruchu cząsteczek

Model teoretyczny płynu jest ośrodkiem (ciałem) ciągłym tj. tworzy tzw. kontinuum materialne

Płyn jest materią ciągłą wypełniającą przestrzeń w sposób doskonale ciągły.

Uproszczenie to jest dopuszczalne - przestrzeń zajęta przez płyn jest nieskończenie wielka w stosunku do wymiarów cząsteczek, zaś wielkości parametrów charakteryzujące ruch płynu przedstawiają wartości przeciętne (średnie)

Element płynu - myślowo wyodrębniona część masy płynu o wymiarach nieskończenie małych w porównaniu do wymiarów masy bedącej w ruchu albo do wymiarów ciał poruszających się w płynie., a równocześnie dostatecznie duzych w porównaniu z wymiarem drogi swobodnej cząsteczki

Liczba Knudsena:

λ- średnia droga swobodna molekuł gazu tj. droga między dwoma kolejnymi zderzeniami molekuł np.

dla powietrza λ=0.06 μm w warunkach normalnych tj. temperaturze 0ºC i ciśnieniu 0.1 Mpa, na wysokości 200 km średnia droga swobodna wynosi λ=18 m.

L - wymiar liniowy zbiornika lub opływanego ciała

 Dla Kn <0.1 można nie uwzględniać molekularnej struktury gazu i traktować gaz jako ośrodek ciągły

V=1 μm3 zawiera 2.7 *10⁶ molekuł

SIŁY DZIAŁAJĄCE NA PŁYN

Siły wewnętrzne - wzajemne oddziaływanie elementów mas wewnątrz obszaru napełnionego płynem, są to siły powierzchniowe 

Siły zewnętrzne - działanie mas nie należących do wydzielonego układu (obszaru) wypełnionego płynem  

Siły masowe

Siły powierzchniowe

SIŁY MASOWE

działające na odległość działają na wszystkie elementy obszaru płynnego np. siła ciężkości są to proporcjonalne do masy elementu dm, na który działają

wektor F - współczynnik proporcjonalności ma wymiar przyspieszenia dla siły ciężkości - wektor przyspieszenia ziemskiego g

SIŁY POWIERZCHNIOWE

Bezpośrednio przyłożone do powierzchni obejmującej wydzieloną część ośrodka

Reakcje hydro- aerodynamiczne między płynem a poruszającym się w nim ciałem stałym

 

Δp' - główny wektor sił działających na element powierzchni o polu ΔS w punkcie M na powierzchni S

Obliczmy

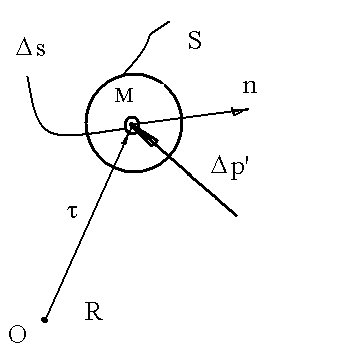
jednostkowa siła powierzchniowa lub naprężenie sił powierzchniowych

Wektor siły powierzchniowej P= pdS iloczyn wektora naprężeń przez pole elementu powierzchniowego

Różnice pomiędzy silą masową i powierzchniową 

F - siła masowa = f(x,y,z,t) jednoznaczna funkcja przestrzeni i czasu, pole wektorowe

p - naprężenie wewnętrzne przybiera w każdym punkcie ośrodka nieskończenie wiele wartości w zależności od kierunku elementu powierzchniowego w danym punkcie w którym przyłożona jest siła jednostkowa

p - funkcja wektora promienia R i wektora n normalnej do elementu powierzchniowego obejmującego ten punkt. Ze zmianą położenie punktu i zmianą kierunku normalnej n ulega zmianie naprężenie p, jego wartość liczbowa i kierunek.

Siła ciśnieniowa - Parcie

 Całkowita siła normalna na skończona powierzchnię S

całkowita siła styczna

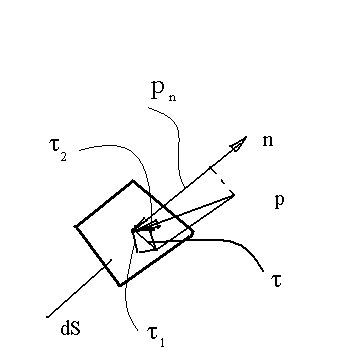
Pole sił powierzchniowych jest polem tensorowym podczas ruch płynu nielepkiego lub dla cieczy w spoczynku jednostkowa siła powierzchniowa pn=-np.

dla całej powierzchni

KLASYFIKACJA PÓL

- skalarne

-   wektorowe

-    tensorowe

 Pole - obszar w mechanice płynów, w którym wielkość fizykalna jest ciągła funkcją punktu

Jeżeli w każdym punkcie pola wartość fizykalna H nie zależy od czasu t

-pole ustalone lub stacjonarne

-pole nieustalone ( niestacjonarne)

H nie zależy od współrzędnych x,y,z - pole jednorodne

H zależy od współrzędnych x, y, z - pole niejednorodne

H=H(x,y,z) - pole przestrzenne

-pole płaskie (dwuwymiarowe)

gdy H(s,t) - zależy tylko od jednej współrzędnej - pole jednowymiarowe

MODELE PŁYNÓW

korzysta się z nich przy rozważaniach problemów mechaniki płynów

 1)  Płyn doskonały - nieściśliwy i nielepki

2) Płyn nieściśliwy i lepki - ciecz rzeczywista oraz gaz przy małych prędkościach

3)   Płyn ściśliwy i nielepki - gaz doskonały

4)   Płyn ściśliwy i lepki - gaz rzeczywisty

MODEL OŚRODKA CIĄGŁEGO

Makroskopowe własności ośrodka ciągłego jako ciągłe funkcje przestrzeni i czasu

 Np. ciśnienie p=p(t,x,y,z)

Prędkość V=V(t,x,y,z), temperatura T=T(t,x,y,z)

Daje to możliwość zastosowania ogólnych twierdzeń teorii pola, tj. mówimy pole ciśnienia, pole temperatury, pole prędkości, pole gęstości

 Parametry te są dostrzegalne przez zmysły człowieka i mierzalne w drodze pomiarów, mimo to wynikają one z mikrostruktury materii.

Jest to tzw. fenomenologiczny sposób opisu zjawisk zachodzących między molekułami

GĘSTOŚĆ PŁYNU

przy Δτ→0, ale zawiera wciąż punkt A, granicę tę nazywamy gęstością płynu w punkcie A(x,y,z).

Gęstość ρ jest skalarem

Objętość Δτ - Δm masa zawarta w tej objętości

PARAMETRY OPISUJĄCE STAN PŁYNU

Prędkość u, ciśnienie p, Gęstość ρ,

temperatura T

Te parametry opisują stan płynu w punkcie ( w elemencie)

Parametry opisujące właściwości transportu wywołane chaotycznym ruchem molekuł

Dynamiczny współczynnik lepkości- μ- transport pędu

Współczynnik dyfuzji- D- transport masy

Współczynnik przewodnictwa cieplnego- λ- transport ciepła (energii)

Parametry zależne od struktury materii

Ciepło właściwe przy stałym ciśnieniu- cp

Ciepło właściwe przy stałym ciśnieniu- cv

Ciepło właściwe dla cieczy- cp=cv=c

Wykładnik izentropy- κ=cp/cv

ELEMENTARNA KINETYCZNA TEORIA GAZÓW 

Niech w 1 m3 gazu znajduje się n cząsteczek

1/3 z nich niech porusza się równolegle do jednej osi x, y, z wzdłuż dodatniego kierunku tej osi tylko 1/2 , a zatem ½ n/3= n/6 jeżeli cząstka ma prędkość c, to wszystkie cząstki zawarte w sześcianie o długości c i polu 1 m2 uderzą w ciągu 1 sek o powierzchnię ścianki naczynia , liczba cząstek nc/6 uderza o ściankę , po odbiciu od ścianki ma pęd -mc, a zatem zmiana pędu Δp=2mc zatem siła bombardowania ścianki

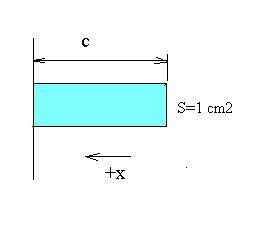
jest to nic innego jak elementarne wyprowadzenie wzoru na ciśnienie na podstawie najprostszej kinetycznej teorii gazów

Wyznaczmy prędkość cząsteczek powietrza:

dla powietrza p=105 Pa, ρ=1.29 kg/m3

Prędkość cząstek (molekuł) gazu z powyższego wzoru można wyznaczyć

(Równa prędkości kuli karabinowej)

Poczyniono tu jednak niesłuszne założenie, że prędkość cząstek jest stała, w rzeczywistości jest pewien rozkład prędkości zwany rozkładem Maxwella

Rozkład Maxwella

skąd dalej średnia prędkość cząsteczek

k- stała Boltzmana , R - stała gazowa dla jednego mola gazu, N-liczba Avogadro

Rozmiary cząsteczek (oszacowanie)

Założenia

-   zasięg oddziaływania między dwiema cząsteczkami wynosi d

-   siła przyciągania ma stałą wartość f, jeżeli odległość jest mniejsza od d, a równa się zeru gdy L>d

CIEPŁO PAROWANIA

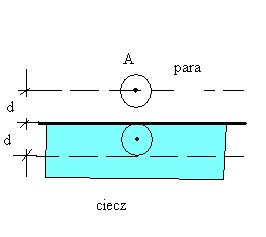
w procesie parowania cieczy cząstka musi pokonać przyciąganie cząsteczkowe na drodze 2d wykonuje więc pracę

zatem praca jednostkowa na 1g wynosi

m - masa cząsteczki

NAPIĘCIE POWIERZCHNIOWE

szukamy wartości pracy wykonanej przy przenoszenia czątsteczek z wnętrza cieczy dla wytworzenia 1 cm2 nowej powierzchni swobodnej na odległości L>d f=0 zaś dla L<d f = const

aby powiększyć swobodna powierzchnię cieczy o 1 cm2 musimy przenieść z głębi cieczy na powierzchnię n cząstek

 

ponadto każda cząsteczka pokonuje przy tym siłe f na drodze d/2 a zatem praca potrzebna do wyniesienia jednej cząstki na powierzchnię

zaś praca na utworzenie 1 cm2 powierzchni wynosi

ŚREDNIA DROGA SWOBODNA (OSZACOWANIE)

walec o promieniu r, cząstka zderzy się z drugą cząstka o ile znajdzie się w tym walcu o objętości V

jeśli n cząsteczek w 1cm3 to ilość zderzeń

średnia droga swobodna jako średnia droga pomiędzy zderzeniami, ale liczba zderzeń to

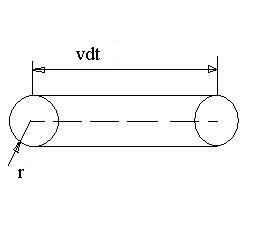
Rys.Walec wymiatany przez cząsteczkę w czasie ruchu

a zatem średnia droga swobodna l

 

(√2 dla rozkładu Maxwella )

aby wyznaczyć, średnią drogę swobodna musimy znać wartości n i r

Wiemy, że w warunkach normalnych 1 mol gazu zajmuje objętość 22.4 l i zawiera N =2*1024 cząsteczek gazu

a zatem ilość cząsteczek w 1 cm3 wynosi

na 1 cm3

 skąd średnia droga swobodna w gazach w warunkach normalnych

ZJAWISKA TRANSPORTU

Lepkość gazu - obecność gradientu prędkości, ruch postępowy warstw gazu względem siebie

U równoległość, U<<c

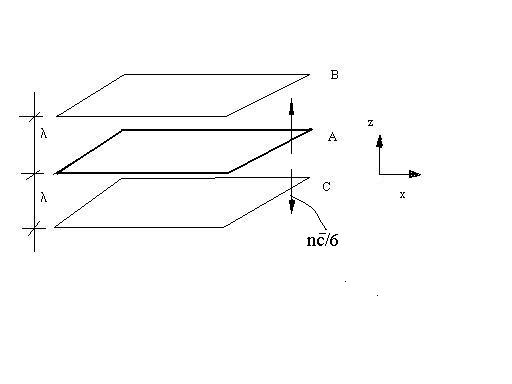
pęd przenoszony przez 1 cm² płaszczyzny A w ciągu jednej sek

naprężenia styczne

µ-dynamiczny współczynnik lepkości

 

 

 n λ- stałe i niezależne od ciśnienia, lepkość nie zależy od ciśnienia i gęstości

( naprawdę zależy, ale w niewielkim stopniu)

DYFUZJA

Obecność gradientu gęstości 

ilość cząsteczek przenoszonych z płaszczyzny B i C do pł.A

współczynnik dyfuzji [m2/s]

znak minus oznacza, że przepływ następuje z obszarów o większej koncentracji do obszarów o mniejszej koncentracji.

PRZEWODZENIE CIEPŁA (ENERGIA WEWNĘTRZNA)

Obecność gradientu temperatury e=cvT, cv ciepło właściwe przy stałej objętości przyrost energii wewnętrznej

Współczynnik przewodności k ściśle związany z lepkością dynamiczną,

k- współczynnik przewodnictwa cieplnego, μ- współczynnik lepkości dynamicznej

PARAMETRY GAZÓW ZALEŻNE OD STRUKTURY MOLEKUŁY

Z kinetycznej teorii gazów

Zasada ekwipartycji energii

 

skąd

gdzie

k - stała Boltzmana, R- stała gazowa,

N - liczba Avogadro

średnia energia na trzy stopnie swobody dla ruchu translacyjnego

gaz jednoatomowy posiada trzy stopnie swobody

suma energii kinetycznej na jeden mol

czyli:

ciepła właściwe przy stałej objętości

f-ilość stopni swobody 

dla gazu jednoatomowego f=3

cv = 3fNk/2=12.5 kJ/(kmol deg)

dla gazu dwuatomowego f=5

cv = 5fNk/2=20.8 kJ/(kmol deg)

ciepło właściwe przy stałym ciśnieniu

 cv = (f+2)Nk/2=12.5 kJ/(kmol deg)

 κ=cp/cv=(f+2)/f κ - wykładnik izentropy

κ=1.66 f=3 gaz jednoatomowy

κ=1.4 f=5 gaz dwuatomowy

κ=1.33 f=6 powietrze

ZALEŻNOŚCI POMIĘDZY PODSTAWOWYMI PARAMETRAMI PŁYNU

Dla gazów doskonałych, f(T, p, ρ)=0 równanie stanu (równanie termiczne)

 Formy tego równania

gdzie R= 8, 314 kJ/kg deg, R - uniwersalna stała gazowa

V- objętość i masa gazu

m - masa gazu o objętości V

T - temperatura gazu w K

n - ilość kilo moli gazu, ρ - gęstość gazu

M - masa molowa gazu

R'=R/M - indywidualna stała gazowa, R'=287 J/kg deg dla powietrza

PRAWA GAZOWE

1) Prawo Boyle'a - Mariotte'a

T = idem , pV=poVo= idem

ၥ- współczynnik ściśliwości gazu

 2) Prawo Gay-Lussaca (pierwsze)

 p=idem

ၡ - współczynnik rozszerzalności termicznej gazu

3) dla V = idem

β- współczynnik rozprężliwości gazu

4) połączone prawo Boyle'a-Mariotte'a - Gay-Lussaca

 

 

R - stała gazowa

Ogólnie

Współczynniki ၡ, ၢ i ၥ są funkcjami T i p dla gazów,

natomiast dla ciał stałych i cieczy są prawie stałe.

GAZY RZECZYWISTE

Dla ciśnienia atmosferycznego oraz temperatur znacznie wyższych od temperatury krytycznej obowiązuje równanie stanu dla gazu doskonałego

Dla dużych ciśnień i niskich temperatur

 

B,C, ..., B', C', ... współczynniki wirialne, funkcje temperatury i rodzaju gazu

 Zwykle wystarcza uwzględnienie tylko jednego ze współczynników B lub B'

Równanie van der Walsa

a, b - stałe uwzględniające odchyłki od stanu gazu doskonałego

ZALEŻNOŚCI DLA CIECZY

Brak równania stanu !!!

·Dla p = const - równanie rozszerzalności termicznej

 

lub

 

·Dla T=const

 

lub

 

·dla v = const

lub

zmienne p, t i V związane są z równaniem stanu f(T, p, ρ)= ∞, stąd

zależność wiążąca te trzy współczynniki

MODUŁ SPRĘŻYSTOŚCI (ŚCIŚLIWOŚCI)

objętość właściwa:

Prędkość dźwięku w wodzie

Gęstość wody

PRĘDKOŚĆ DŹWIĘKU DLA GAZU

dla gazu

moduł sprężystości (ściśliwości)

prędkość dźwięku

  

TWIERDZENIA CAŁKOWE ANALIZY WEKTOROWEJ.

Przekształcenia Greena całek powierzchniowych strumienia skalara ၡ i wektora a

1)Strumień skalara przez powierzchnię zamkniętą ၳ równy jest całce objętościowej gradientu skalara po objętości V objętą tą powierzchnią.

2) Strumień wektora a przez powierzchnię zamkniętą ၳ jest równy całce objętościowej z dywergencji wektora a po obszarze ograniczonym tą powierzchnią.

Twierdzenie Greena Gaussa-Ostrogradskiego

Strumień iloczynu wektorowego wektora jednostkowego n i wektora a przez zamkniętą powierzchnię ၳ jest równy całce objętościowej rotacji wektora po objętości zamkniętej tą powierzchnią.

Dla tensora A można napisać uogólnione twierdzenie Greena - Gaussa - Ostrogradskiego

Strumień tensora A przez zamkniętą powierzchnię ၳ równy jest całce objętościowej dywergencji tensora A po objętości zawartej w powierzchni ၳ.

Twierdzenie Stokes'a (przekształcenie Kelvina)

Całka krzywoliniowa wektora a po krzywej zamkniętej c równa się strumieniowi

rotacji wektora a przez powierzchnię zamknięta ၳ której brzegiem jest kontur c

(rozpiętą na konturze c)

Twierdzenie transportu

Twierdzenie to dotyczy zmian w czasie wielkości polowej w pewnej skończonej

objętości płynu V, w odróżnieniu od zmian w nieskończenie małym elemencie płynu.

Objętość ta mimo, że zawiera wciąż te same elementy płynu, może zmieniać się

w czasie i w przestrzeni.

Szybkość zmian tej wielkości polowej ၰ w objętości V będzie określała

pochodna substancjalna.

Trzy różne formy twierdzenia transportu

Korzystając ze wzoru na pochodną substancjalną

Korzystając dalej ze wzoru თბ(ၰ u) = uၰბთ + თბၰu,

gdzie ၰ - skalar, wektor lub tensor

Korzystając następnie z przekształcenia Greena - Gaussa - Ostrogradskiego mamy

KINEMATYKA PŁYNÓW

Linia prądu - linia pola wektorowego prędkości

 Linia pola wektorowego - styczna do wektora pola odpowiadającego temu punktowi

Pole prędkości v = v(x, y, z, t)

Składowe vx = vx (x, y, z, t), vy = vy (x, y, z, t), vz = vz (x, y, z, t)

Element linii prądu ds = ds (dx, dy, dz)

Równanie linii prądu - iloczyn wektorowy

v Ⴔ ds = 0

albo

W wyniku całkowania układu równań otrzymujemy następujące związki

Są to równania rzutów linii prądu na płaszczyzny układu współrzędnych. Dwa tylko z nich są niezależne. Stałe c1, c2, c3 zależą od wyboru punktu m0 (x0, y0, z0). Czas t odgrywa rolę parametru. Kształt linii prądu zależy od czasu, tylko w ustalonym polu prędkości kształt linii prądu jest niezmienny.

Powierzchnia prądu - powierzchnia utworzona z linii prądu, przecinająca dowolną linię, nie będącą linią prądu.

Rurka prądu - jeśli ta dowolna linia jest linią zamkniętą

Tor elementu - linia wzdłuż której porusza się element płynu (traktowany tutaj jako punkt)

 

Równanie różniczkowe toru

lub

Równanie podobne - ale czas t nie jest tutaj parametrem ale zmienną jak x, y, z

Całkując otrzymamy:

F1(x, y, c1) = 0 F2(y, z, c2) = 0

F3(z, t, c3) = 0 F4(t, x, c4) = 0

Trzy z czterech związków są niezależne, rugując czas otrzymamy trzy równania rzutów toru elementu płynu na płaszczyzny x, y, z.

W ustalonym polu prędkości kształt linii prądu przechodzącej przez dowolny punkt przestrzeni jest identyczny z kształtem toru każdego elementu płynu, przechodzącego przez ten punkt.

Twierdzenie. Tor elementu płynu jest obwiednią linii prądu przechodzących przez punkty toru odpowiadające chwilowym położeniom elementu.

Przez każdy punkt pola prędkości przechodzi w każdej chwili t na ogół jedna tylko linia prądu i jeden styczny do niej w tym punkcie tor - jeśli tylko współrzędne kierunkowe wspólnej stycznej są w każdym punkcie i w każdej chwili jednoznacznie określone.

 

Wyjątek: Punkty spiętrzenia - punkty pola prędkości

 v(x, y, z, t) = 0, współczynniki stycznej nieokreślone

 Punkty spiętrzenia - punkty osobliwe (z matematycznego punktu widzenia).

ZMIENNE LAGRANGE'A I ZMIENNE EULERA

Dwa kąty widzenia ruchu płynu: zwane od nazwisk swych twórców

 

Metoda Lagrange'a

 Badanie i opis właściwości fizycznych poruszającego się indywidualnego elementu płynu jako punktu materialnego.Specjalne zmienne - tzw. zmienne Lagrange'a indywidualizujące element płynu, stałe dla każdego elementu płynu, niezależne od czasu i zmiany położenia

 W konsekwencji otrzymamy opis ruchu w postaci funkcjiH = H(a, b, c, t),

gdzie a, b, c, t - zmienne Lagrange'a

 Zmiana a, b, c - powoduje przejście do innego elementu płynu,

zmiana t - zmiana wielkości H w elemencie płynu.

 Równania toru elementu płynu

 x = x(a, b, c, t ) y = y(a, b, c, t) z = z(a, b, c, t)

Prędkość i przyspieszenie

Metoda Eulera - badanie i opis zmian wielkości fizycznych charakteryzujących ruch płynu w poszczególnych punktach przestrzeni (ustalonych punktach przestrzeni)

x, y, z, t - zmienne Eulera

 

H = H(x, y, z, t) - metoda Eulera polega na badaniu pól wielkości fizycznych

 Zwykle badamy przepływy metodą Eulera

 Przejście pomiędzy obu układami

 

Warunek - wyznacznik funkcyjny jakobian różny od zera w żadnym punkcie obszaru

POWIERZCHNIA KONTROLNA

Powierzchnia kontrolna - otwarta lub zamknięta powierzchnia w polu prędkości płynu, położenie każdego jej punktu nie ulega zmianie względem układu odniesienia z upływem czasu.A więc tworzą je wciąż te same punkty przestrzenne, natomiast znajdują się w niej coraz to inne elementy płynu.

w zmiennych Eulera Fk(x, y, z) = 0, Dla zmiennych Eulera - zależność od czasu

 

Fp(a(x, y, z, t), b(x, y, z, t), c(x, y, z, t)) = 0.

 

Dla zmiennych Lagrange'a

 Fk[x(a, b, c, t), y(a, b, c, t), z(a, b, c, t)] = 0

 A więc zależność powierzchni kontrolnej od czasu.

 

Obszar kontrolny - obszar ograniczony zamkniętą powierzchnią kontrolną.

 Powierzchnia płynna - otwarta - zamknięta powierzchnia w polu prędkości płynu, tworzą je wciąż te same elementy płynu natomiast zmienia się jej położenie względem układu odniesienia x, y, z a także jej kształt

Cyrkulacja wektora

Cyrkulacja wektora pola H wzdłuż łuku AB a więc całka iloczynu skalarnego H·ds,

ds - skierowany element łuku AB

Linia wirowa

Linia pola wektorowego rotacji według równania

Zbiór linii wirowych - powierzchnia wirowa (ale linia ta nie jest linią wirową)

Rurka wirowa - gdy powierzchnia wirowa zamknięta.

 

Drugie twierdzenie Helmholtza - strumień rotacji przez dowolny przekrój poprzeczny rurki wirowej jest w każdej chwili jednakowy

Prawo Biota-Savarta

dotyczy pola prędkości w sąsiedztwie włókna wirowego

 

 

i w formie różniczkowej:

RUCH LOKALNY PŁYNU

Ruch punktów elementu płynu względem bieguna dowolnie wybranego w rozpatrywanym elemencie płynu

dၲ = [v(r + ၲ) - v(rP)] dt

ၲ - promień

TWIERDZENIE HELMHOLTZA

Prędkość dowolnego punktu A elementu płynu jest sumą vp prędkości bieguna P i prędkości względnej, równej ၲႴၷ obrotu prędkości jako ciała sztywnego i prędkości deformacji vd.

Równanie ZACHOWANIA MASY i równanie CIĄGŁOŚCI

Równanie zachowania masy jest ogólnym prawem przyrody, postulatem mówiącym, że materia nie znika i nie tworzy się z niczego.Dla objętości płynu zawierającej wciąż te same cząstki płynu postulat ten można zapisać

 

m i ၲ odpowiednio masa i gęstość

Korzystając następnie z równań analizy wektorowej można równanie to przedstawić w różnej formie

 

 lub z wykorzystaniem pochodnej substancjalnej

 

Gdy gęstość nie jest zależna od czasu

 

Postać całkowa równania zachowania masy

 

 

Jest często wykorzystywana do sporządzenia bilansu masy w objętości kontrolnej V całkując po powierzchniach ograniczających ၳ.

 

W szczególności, gdy gęstość nie jest funkcją czasu otrzymamy

PRAWA EULERA

Prawa Eulera

Całkowita siła powierzchniowa działająca na płyn o objętości V i powierzchni ograniczającej ၳ równa jest

 

natomiast całkowita siła zewnętrzna działająca na płyn o objętości V dana jest następującym wzorem

Zasada zachowania pędu postuluje, że suma obu tych sił jest równa różniczce względem czasu pędu płynu.

A zatem:

1. prawo Eulera:

Rozważmy dalej moment obrotowy a w szczególności jego bilans na elemencie płynu

2. prawo Eulera:

 

Suma momentów obrotowych działających na element płynu o objętości V i ograniczonego powierzchnią ၳ jest równa różniczce względem czasu momentu pędu płynu.

Prawa Eulera są rozszerzeniem praw Newtona dotyczących materialnego sztywnego punktu na przypadek ruchu ośrodka ciągłego.

PRAWA CAUCHY'EGO

Pierwsze prawo Cauchy'ego jest odpowiednikiem pierwszego prawa Eulera przy czym zamiast wektorem naprężeń to operuje składowymi tensora naprężeń T

Korzystając z twierdzenia Greena - Gaussa - Ostrogradskiego możemy napisać

 

Podstawiając do równania Eulera otrzymamy

 

Wykorzystując dalej wzory z poprzednich rozdziałów, w szczególności równanie ciągłościთ ბT dywergencja tensora jest wektorem

Jest to równanie ruchu płynu, nazywane też równaniem różniczkowym bilansu pędu lub też pierwszym prawem Cauchy'ego. Są to w zasadzie trzy równania na każdą składową wektorową თბT = Tij, i

DRUGIE PRAWO CAUCHY'EGO

Drugie prawo Cauchy'ego jest odpowiednikiem drugiego prawa Eulera i dotyczy bilansu momentu obrotowego obszaru płynnego zapisanego przy wykorzystaniu składowych tensora naprężeń. Po pewnych przekształceniach otrzymamy

 

Na mocy pierwszego prawa Cauchy'ego lewa strona jest równa zeru, skąd natychmiast wypływa wniosek

ၥijk Tij = 0

a więc Tij = Tji

  Jest to zapis drugiego prawa Cauchy'ego, że warunkiem koniecznym i dostatecznym zachowania momentu obrotu w płynie jest symetria tensora naprężeń. Konsekwencją tego prawa jest wniosek, że do pełnego określenia tensora naprężeń w płynie wystarczy znajomość sześciu z dziewięciu jego składowych tzn. trzech normalnych i trzech stycznych.

CIŚNIENIE HYDROSTATYCZNE

Nazywamy naprężenie normalne do elementarnej powierzchni i niezależne od jej orientacji

 

Cieśn. hydrostatyczne - p jest niezależne od n.

Wydzielając z tensora naprężeń Tij ciśnienie hydrostatyczne otrzymamy tensor naprężeń lepkich Pij

Dla płynu w spoczynku P_ij=0 (brak odkształceń) 

Wtedy

jest ciśnieniem hydrostatycznym dla płynu nieściśliwego.

Dla płynu ściśliwego w spoczynku p jest równoznaczne z ciśnieniem termodynamicznym albo raczej termostatycznym.

 W ogólniejszym przypadku wartość średnia naprężeń normalnych wynosi

PŁYN STOKESOWSKI

Dla płynu stokesowskiego tensor naprężeń

 

 i jest ciągłą funkcją tensora deformacji D i lokalnego stanu termodynamicznego (ciśnienia p). Tensor naprężeń Tij w płynie stokesowskim nie zależy jawnie od położenia r, a zatem płyn jest homogeniczny.Płyn stokesowski jest ponadto izotropowy tzn. ma jednakowe właściwości we wszystkich kierunkach.Jeśli w płynie nie ma deformacji, to tensor naprężeń lepkich jest równy zeru, a naprężenie jest ciśnieniem hydrostatycznym lub termostatycznym.

Tensor naprężeń lepkich

 

Z warunku na znikanie Pij= 0 gdy Dij= 0 wynika również ၡ = 0

Zatem:

PŁYN NEWTONOWSKI

Jest to liniowy płyn stokesowski, a więc ၧ = 0

Tij = (-p+ၡ)I + ၢ D

Tensor naprężeń lepkich:

Pij = ၬ(თბ u) ၤij + 2ၭ Dij

ၭ - współczynnik proporcjonalności, lepkości

 Tensor naprężeń: Tij = (-p + თბၬ u) I + 2ၭ Dij

 Przy omawianiu ciśnienia hydro- i termostatycznego powiedziano, że wartość średnia naprężeń normalnych wynosi

Dla płynu nieściśliwego div u = 0, თბ u = 0

Zatem

i równa się ciśnieniu hydrostatycznemu.

RÓWNANIE RUCHU PŁYNU NEWTONOWSKIEGO

Pierwsze równanie Cauchy'ego jest równaniem ruchu płynu

 

nie wyróżniającym żadnego modelu płynu. 

Jeżeli podstawimy do niego równanie konstytutywne płynu newtonowskiego, to otrzymamy równania Naviera - Stokes'a opisujące ruch płynu newtonowskiego

Zatem:

CIEPŁO WŁAŚCIWE I ENTALPIA PŁYNU

Zgodnie z definicją

 

Q - ilość ciepła dostarczana na jednostkę masy gazu

T - temperatura

 Wyróżniamy dwie definicje ciepła właściwego w zależności od procesu, w którym dostarczane jest ciepło:

-         ciepło właściwe przy stałej objętości

-         ciepło właściwe przy stałym ciśnieniu

 Pierwsza zasada termodynamiki mówi, że ciepło i energia mechaniczna są

równoważne i konwertowalne

·Dla procesów odwracalnych możemy napisać

v = 1/ၲ - objętość właściwa gazu, e - energia wewnętrzna gazu

·Dla gazów doskonałych energia wewnętrzna jest tylko funkcją temperatury:

 

równanie kaloryczne stanu

·Dla gazów doskonałych mamy również następującą zależność:

 

R - stała gazowa

·Dla procesów izotermicznych całkowite ciepło dostarczone do płynu

Wielkość h jest jedną z funkcji termodynamicznych i nosi nazwę entalpii.

 Składnik p/ၲ ma oczywiście wymiar energii (odniesionej do jednostki masy) i nazywany bywa energią ciśnienia

W ustalonych warunkach pracy maszyny lub urządzenia procesy konwersji energii zachodzą przy stałej temperaturze, a więc izotermicznie, a w takich warunkach entalpia jest szczególnie przydatną funkcją.

RÓWNANIE ENERGII KINETYCZNEJ

 Jeżeli pomnożymy równanie ruchu skalarnie przez prędkość u otrzymamy równanie energii kinetycznej

T - tensor naprężeń

Ponieważ

Zatem

Jeżeli w tensorze naprężeń wyróżnimy część ciśnieniową i część lepką

 Tij = - pၤij + Pij = - pၤij + თბၬ u + 2ၭD

to wtedy

bo p:ბ u = pთბ u

 Co można opisać jako:

 Zmiana energii kinetycznej płynu

jest równa sumie:

ၲ uთ f - pracy sił zewnętrznych

-თბ (pu) - pracy ciśnienia zewnętrznego

ბ (uP) - pracy sił tarcia

pთბ u - energii zamienionej odwracalnie w energię wewnętrzną

-P: ბ u - energii zamienionej nieodwracalnie w energię wewnętrzną 

Składnik

czyli iloczyn tensora naprężeń lepkich i tensora prędkości deformacji nosi nazwę funkcji intensywności dysypacji energii

RÓWNANIE ENERGII

Stosując pierwszą zasadę termodynamiki w takiej formie, że przyrost energii wewnętrznej i kinetycznej w obszarze płynnym jest równy przepływowi (strumieniowi) ciepła do tej objętości i pracy wykonanej W

 

q - źródło ciepła

Stosując twierdzenie Greena - Gaussa - Ostrogradskiego otrzymamy następnie równanie różniczkowe energii

 

 

Jeżeli odejmiemy od tego równania równanie energii kinetycznej (z poprzedniego paragrafu), to otrzymamy równanie na zmianę w czasie energii wewnętrznej elementu płynu:

 

Widzimy zatem, że energia wewnętrzna płynu wzrasta przez:

doprowadzenie ciepła თბ (kბ ၱ) > 0

sprężenie gazu თბ u < 0 oraz

przez dyssypację energii kinetycznej ၆.

W równaniu energii kinetycznej funkcja dyssypacji energii zmniejszała energię kinetyczną, a tutaj zwiększa energię wewnętrzną.

Przy rozprężaniu gazu, gdy თბ u > 0 energia wewnętrzna gazu obniża się i temperatura gazu ၱ obniża się. Składnik reprezentowany funkcją dysypacji ၆ jest zawsze dodatni, niezależnie do procesu (sprężanie lub rozprężanie, podgrzewanie lub schładzanie gazu).W równaniu energii cieplnej (wewnętrznej) i energii kinetycznej dwa składniki są jednakowe  pთბ u i p:ბ u.

Składniki te opisują zatem zamianę energii kinetycznej (mechanicznej) w cieplną.

Składnik pთბ u może być dodatni lub ujemny w zależności od sprężania lub rozprężania płynu.

Składnik ten opisuje zatem odwracalny proces przemiany obu form energii, natomiast składnik + p:ბ u jest zawsze dodatni i opisuje przemianę energii mechanicznej w cieplną; jest to proces nieodwracalny.

ZASADA ZACHOWANIA ENERGII CAŁKOWITEJ

Podstawiając do równania energii otrzymamy 

 

Równanie to jest zapisem zasady zachowania energii całkowitej

 

 będącej sumą energii wewnętrznej, kinetycznej i potencjalnej.

PARADOKS NIESTACJONARNOŚCI

Jeżeli dalej - jak się często zakłada - płyn jest nielepki, a więc ၭ = ၬ = 0 oraz nieprzewodzący ciepła k = 0, wtedy

Wniosek: W przepływie izentropowym (bez wymiany ciepła z otoczeniem) cząstka płynu może zmienić swoją entalpię tylko wtedy, gdy ruch płynu jest nieustalony, czyli gdy

czyli istnieje lokalna różniczka

Inaczej mówiąc: W płynie nielepkim transport energii jest możliwy tylko wtedy gdy ruch płynu jest nieustalony.

Jeśli natomiast założymy, że

to oznacza, że maszyna, w której przepływ jest nielepki, adiabatyczny i ustalony nie daje zmiany entalpii całkowitej, a więc nie daje pracy, bo

Większości maszyn, za wyjątkiem pomp oporowych i turbin, gdzie siły lepkości użyto w zamierzony sposób, efekty lepkości są małe i w pierwszym przybliżeniu pomijalnie małe.

Ponadto zakłada się, że przepływ jest adiabatyczny, zatem bez wymiany ciepła z otoczeniem i wtedy q = 0.

Można to nazwać paradoksem nieustaloności (niestacjonarności) albo wręcz problemem istnienia maszyn przepływowych.

Zmiana entalpii całkowitej płynu w czasie jest równa lokalnej zmianie w czasie ciśnienia statycznego

ENTROPIA

Równanie entropii

 Równanie energii wewnętrznej

 

można napisać inaczej, a mianowicie

 

ၱ - temperatura

Z termodynamiki znana jest relacja Gibasa

 

gdzie s jest entropią obszaru płynnego

(I) Zatem równanie

opisuje zmianę w czasie entropii płynu

 

Bilans entropii (równanie)

W objętości płynnej V możemy zmianę entropii napisać

wg znanych już wzorów analizy wektorowej

Jeśli w obszarze płynu są źródła entropii w czasie S, a na powierzchni ograniczającej ၳ mamy strumień ciepła q i temperaturę ၱ, to możemy napisać również:

ZAGADNIENIE PRZEPŁYWOWE

Postawienie zagadnienia przepływowego i sformułowanie równań nie oznacza jeszcze znalezienia ich rozwiązań, ale jest na pewno wstępem do rozwiązania zagadnienia przepływowego

Często w celu rozwiązania zagadnienia przepływowego decydujemy się na znaczne uproszczenia wyżej podanych równań

Uproszczenia te polegają przede wszystkim na:

1)Wybraniu specjalnych przypadków równania konstytutywnego lub równania stanu np. płyn newtonowski, płyn nielepki, gaz doskonały itp.

2)Wybraniu specjalnych równań ruchu np. ruch ustalony, hydrostatyka, równania warstwy przyściennej

3)Wybraniu specjalnych rodzajów ruchu np. ruch bezwirowy, ruch płaski (dwuwymiarowy), ruch osiowosymetryczny

PODSTAWOWE ZAGADNIENIE MECHANIKI PŁYNÓW

Równanie ciągłości

Równanie ruchu

Równanie energii

Równanie momentu ruchu wykorzystano do ustalenia symetryczności tensora naprężeń T

1)Równanie stanu

ၲ = ၲ(R, ၱ, p), p = ၲ R ၱ , ၲ = const

ၲ = ၲ(p) barotropowy płyn

2) Równanie wytwarzania energii

3) Pole sił masowych

q = q(ၲ, ၱ, p, t)

F(Fx, Fy, Fz) = F(x, y, z, t) znane pole

q = 0

F=0,

Strumień ciepła przechodzący przez powierzchnię ciała stałego określa się na powierzchni ciała zakładając rozkład temperatury, bądź składową gradientu temperatury w kierunku prostopadłym do powierzchni.

-ścianka izolowana tj. nieprzenikalna dla ciepła

- stała temperatura powierzchni ciała

q=const - stały strumień ciepła na powierzchni

STATYKA PŁYNÓW

Gdy u = 0

równanie wektorowe

równanie równowagi Eulera

I trzy równoważne równania skalarowe

Natomiast równanie ciągłości i energii są spełnione tożsamościowo

Statyka płynów zajmuje się zagadnieniami równowagi i stateczności płynów nieruchomych względem przyjętego układu odniesienia, a także zajmuje się siłami wywieranymi na ściany zbiorników i na ścianki ciał pogrążonych w płynie i będących w spoczynku względem płynu  

Statyka płynu lepkiego i nielepkiego jest identyczna

Najprostszy przypadek, na płyn nie działają siły masowe F Ⴚ 0

wtedy równanie równowagi ბ p = 0

 

Matematyczny zapis prawa Pascala - ciśnienie jest stałe w całej masie płynu, jeśli nie działają na płyn siły masowe.Prawo Pascala można zastosować w przybliżeniu do płynów pod działaniem sił masowych, jeśli siły masowe są pomijalnie małe w stosunku do sił ciśnieniowych, np. w prasach mechanicznych, sprężarki tłokowe i wszystkie urządzenia zawierające płyny pod dużymi ciśnieniami

Warunek na pole sił masowych, aby płyn był w równowadze

Jeśli płyn jest barotropowy ၲ = ၲ(p)

( ၲ = const szczególny przypadek barotropowości ),

wtedy istnieje tzw. funkcja ciśnienia

skąd mamy zależność

Podstawiając do równania równowagi F =ბ P

Zatem pole sił F musi być potencjalne, zatem F =ბ U,

U - potencjał sił masowych jednostkowych

Wniosek: Płyn barotropowy, a więc również ciecz, może znajdować się w równowadze tylko w polu potencjalnym sił masowych jednostkowych.

Potencjał masowych jednostkowych sił musi być równy funkcji ciśnienia

(z dokładnością do stałej addytywnej).

Powierzchnie równego potencjału U(x, y, z) = const nazywamy powierzchniami ekwipotencjalnymi.

Pole grawitacyjne ziemskie jest polem potencjalnym.

PŁYN BAROKLINOWY

Płyn baroklinowy - gdy gęstość zależy nie tylko od ciśnienia

Dla płynu baroklinowego - może on być w równowadze również w polu niepotencjalnym.

Obliczmy Ⴔბ (ၲ F) = Ⴔბ (ბ p)

=> Ⴔბ (ၲ F) = 0

(ბ p) = 0

ale Ⴔბ (ၲ F) = Ⴔბၲ F + ბ ၲ Ⴔ F = 0 /თ F

mnożąc skalarnie

Fბთ F = 0 bo (ბ ၲ Ⴔ F)თ F = 0 bo jest to iloczyn skalarny prostopadłych wektorów

Co oznacza, że pole sił masowych jednostkowych posiada rodzinę powierzchni ekwipotencjalnych.

Pole F jest prostopadłe do składowych tensora ბ F . Warunek ten jest ogólniejszy od warunku potencjalności pola. Warunek ten spełnia każde pole potencjalne.

POWIERZCHNIA EKWIPOTENCJALNA

Właściwości powierzchni ekwipotencjalnej

 Gęstość płynu nie zmienia się wzdłuż powierzchni ekwipotencjalnej

Powierzchnia ekwipotencjalna jest też powierzchnią izosteryczną.

Powtórzmy

Ⴔბ (ၲ F) = Ⴔბၲ F + ၲბ Ⴔ F = 0

aleბ ၲ Ⴔ F = 0 =>ბ ၲ Ⴔ ბ U = 0

 Wektor ბ ၲ jest prostopadły do ბ U powierzchni ekwipotencjalnej.

  Ciśnienie płynu nie zmienia się wzdłuż powierzchni ekwipotencjalnej 

ၲ F = ბ p jeśli F = ბ U to ბၲ U = ბ p

 Swobodna powierzchnia cieczy jest powierzchnią ekwipotencjalną.

Wszak jest ona izobaryczna (o stałym ciśnieniu).

POLE GRAWITACYJNE

Na biegunach g = 9,832 m/s2 , na równiku g = 9,780 m/s2

Kierunek przyspieszenia jest normalny do powierzchni Ziemi (nie przechodzi zatem dokładnie przez jej środek).

Dla uproszczenia zakładamy, że Ziemia jest kulą o R = 6370 km, że g0 = 9,81 m/s2 jest stałe i przechodzi przez środek Ziemi, a ponadto, że przyspieszenie ziemskie maleje z kwadratem odległości od środka Ziemi

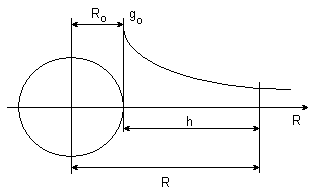
Rzeczywiste ziemskie pole grawitacyjne

  Jeśli wymiary zbiorników cieczy lub mas atmosfery są małe w porównaniu z wymiarami Ziemi, to zmienność przyspieszenia g z wysokością i zmianę kierunku można pominąć.

Wtedy ziemskie pole grawitacyjne traktujemy jako jednorodne a powierzchnię Ziemi jako płaszczyznę normalną do linii pola. Jest to wtedy uproszczone ziemskie pole grawitacyjne.

RÓWNOWAGA CIECZY W UPROSZCZONYM POLU GRAWITACYJNYM

Pole jednorodne, linie pola pionowe, powierzchnia cieczy pozioma - jest to zwierciadło cieczy.

Wtedy równanie

ρdU = dp ma postać ၲ g dz = dp

Jeśli równanie to scałkujemy, zakładając

ၲ = const i p = po na powierzchni zwierciadła, to :p = po + ၲ g z wzór manometryczny

z - oznacza zanurzenia od powierzchni swobodnej (lustra, zwierciadła wody)

ၲ g z = ၧ z - ciśnienie hydrostatyczne

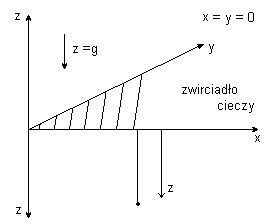
Warunki stateczności w polu potencjalnym.

Stateczność - właściwość stanu równowagi

Układ będący w równowadze nazywamy statecznym wówczas, gdy po wyprowadzeniu go ze stanu równowagi istnieje tendencja powrotu do stanu równowagi.

  Rozważmy stan równowagi płynu w polu potencjalnym

 ၲ F = ბ p równanie równowagi

 F = ბ u warunek równowagi

  Znajdziemy teraz warunki stateczności tego stanu.

Warunki stateczności:

1)Jeśli ρ^'2> ၲ2 to siła działająca na ten element będzie większa niż na sąsiednie elementy o gęstości ၲ 2, a zatem spowoduje dalsze przesunięcie elementu w kierunku n. Zatem płyn jest w równowadze chwiejnej czyli położenie równowagi jest niestateczne

2)Jeśli ρ^'2= ၲ 2 - płyn jest w równowadze obojętnej, charakterystyczne dla cieczy, gdzie ၲ = const

3)Jeśli ρ^'2< ၲ 2 - na element przesunięty działa siła mniejsza niż na elementy sąsiednie, element wróci do swojego położenia wyjściowego, czyli do U = c1 czyli stan równowagi płynu jest stateczny

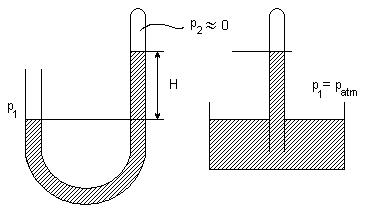
Manometry cieczowe. Jednostki ciśnienia

Manometr - przyrząd do pomiaru różnicy ciśnień. Mierzona różnica ciśnień jest proporcjonalna do długości pewnego słupa cieczy.

Stosując wzór manometryczny dla obu ramion manometru otrzymamy

 p' = p1 + ၲ g h p'' = p2 + (h + h1 + h2)

Powierzchnia ekwipotencjalna jest izobaryczna

p' = p'' i stąd p1 - p2 = ၲ g (h1 + h2)

Miarą różnicy ciśnień w manometrze U - rurkowym jest długość słupa cieczy h1 + h2

Ramiona U - rurki pionowe, gęstość cieczy w manometrze ၲ, a ramiona U - rurki podłączone do zbiorników, w których jest gaz o ciśnieniu p1 i p2

MANOMETR

Manometr z rurką zamkniętą

p2 = próżnia (a w zasadzie ciśnienie par rtęci odpowiadające temp. cieczy)

Barometry do pomiaru ciśnienia atmosferycznego

CIĄG KOMINOWY

Zasada ciągu kominowego -  Ciąg kominowy powstaje wskutek różnicy ciśnień na wlocie i wylocie komina. Różnica ciśnień jest spowodowana różnicą ciężarów zimnego powietrza i słupa gorących spalin w kominie. Jest to ciąg naturalny, oparty na wykorzystaniu energii cieplnej.

Różnica ciśnień - wykorzystana na nadanie prędkości spalinom i na pokonanie oporów przepływu w kominie

ၲsp - gęstość spalin dla temperatury średniej

ၲp - gęstość powietrza

H - wysokość komina

 psp = ၲsp g H

pzp = ၲp g H

၄p = g(ၲp - ၲsp)H,

ၲsp = 1,25 - 0,0027 t, t [oC]

PARCIE PŁYNU NA ŚCIANY CIAŁ STAŁYCH

Parcie płynu -Dowolna powierzchnia materialna ၳ - otwarta lub zamknięta jest ścianą zbiornika zawierającego płyn lub ścianką ciała stałego zanurzonego w płynie

 

n- normalna do powierzchni,zewnętrzna względem płynu

p - ciśnienie na tej powierzchni

 

Parcie elementarne

 

Parcie całkowite

Moment ogólny parć elementarnych

Obliczenie powyższych całek musi być poprzedzone określeniem ciśnienia jako funkcji punktu na powierzchni ၳ.

PARAMETR UKŁADU WEKTORÓW

Parametr układu wektorów

 Iloczyn skalarny sumy wektorów i momentu ogólnego, przy czym moment ogólny stanowi wypadkową momentów poszczególnych wektorów układu względem tego samego dowolnie obranego bieguna.

 ၰ = PთM - parametr układu parć elementarnych

 Jeżeli układ parć elementarnych jest płaski, to ၰ = 0, bo

  Jeżeli ၰ Ⴙ 0 układ sprowadza się do wektora wypadkowego i pary wektorów.

  Jeżeli ၰ = 0, a wypadkowa układu jest różna od zera, to układ sprowadza się do wektora wypadkowego, a moment pary jest w tym przypadku równy zeru

PARCIE NA ŚCIANĘ PŁASKĄ

Szczególny przypadek, technicznie ważny, gdy ၳ jest wycinkiem płaskiej ściany zbiornika zawierającego ciecz o gęstości ၲ nachylonej pod kątem ၡ do zwierciadła wody. Pole grawitacyjne jest oczywiście polem jednorodnym.

0ABC - płaska ściana zbiornika, zakreskowany wycinek - interesująca nas część ściany

 x, y - powierzchnia zwierciadła wody z do powierzchni, a ჺჺ g

  Drugi układ współrzędnych ၸ ၨ ၺ obrócony o kąt ၡ

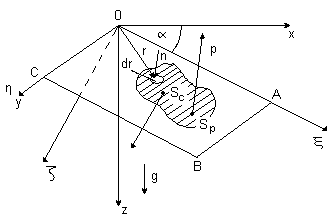
Zbiornik jest otwarty, tj. ciśnienie na powierzchni swobodnej w zbiorniku i na powierzchni zewnętrznej są jednakowe

Różnica ciśnień na wspólnej normalnej do ścianki po stronie zwilżonej i niezwilżonej dana jest zgodnie z wzorem manometrycznym

p = ၲ g z = ၧ z

 a parcie równe jest

moment

 

Normalna n ma stały kierunek, a zatem układ parć elementarnych jest układem równoległym.

 Dla takiego układu parametr ၰ = 0,

ponieważ P Ⴙ 0

  Układ sprowadza się do siły wypadkowej P, moment pary wypadkowej jest równy zeru.

 

PARCIE CIECZY NA ŚCIANY ZAKRZYWIONE

Parametr układu parć elementarnych wywieranych przez ciecz na ścianę zakrzywioną jest na ogół różny od zera, a więc układ sprowadza się do parcia wypadkowego i do pary sił o momencie różnym od zera

 ၰ = PთM Ⴙ 0

Utrzymanie zakrzywionej ściany w równowadze wymaga zatem przyłożenia do niej nie tylko siły przeciwnej parciu wypadkowemu, ale i pary sił o odpowiednim momencie, gdy dla ściany płaskiej do utrzymania jej w równowadze wystarcza siła przeciwna parciu wypadkowemu i przyłożona w środku parcia.

Składowa parcia na ścianę zakrzywioną wzdłuż dowolnej osi pionowej jest równa parciu na ścianę płaską normalną do obranej osi i stanowiącą rzut rozpatrywanej ściany zakrzywionej.

  Składowa pionowa parcia na ścianę zakrzywioną jest równa ciężarowi słupa cieczy o tworzących pionowych znajdujących się nad rozpatrywaną ścianą zakrzywioną.

 Ponieważ pola ၳyz i ၳxz nie zależą od kształtu powierzchni ၳ, więc rzuty na kierunki poziome naporu hydrostatycznego P na ścianę sztywną ၳ nie zależą od kształtu ściany, natomiast zależą od konturu obejmującego ścianę i od jego położenia pod swobodną powierzchnią cieczy.

Linia działania naporu P2 przechodzi przez środek ciężkości danego słupa płynu nad powierzchnią zakrzywioną.

PARCIE NA ŚCIANĘ WALCOWĄ O TWORZĄCEJ POZIOMEJ

AB - ślad przecięcia ściany z płaszczyzną

 Parcie na zakrzywioną powierzchnię walcową sprowadza się do: px i pz

px = ၲ g zsc S

pz = ၲ gV

zsc - głębokość środka geometrycznego figury (rzutu) powierzchni walcowej

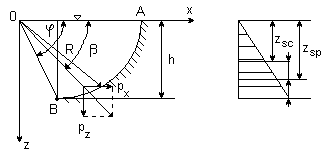
Głębokość środka naporu zsp siły Px obliczamy ze wzoru

Napór całkowity na ścianę walcową o tworzącej poziomej

p = i px + j py

Napór tworzy z osią x kąt ၢ

PARCIE GAZU

Dotyczą te same wzory co parcia cieczy.

W gazach jednak ciśnienie zależy od temperatury. Ponadto gęstość gazów jest wielokrotnie niższa od gęstości cieczy, dlatego też zmiany ciśnienia spowodowane siłami masowymi jednostkowymi mogą okazać się pomijalnie małe. Wtedy ciśnienie w całym obszarze jest stałe, Ⴎ prawo Pascala

p = p1 + ၲ g(z2 - z1),

jeśli

Uproszczone pole grawitacyjne g = const,

bo zmienność ciśnienia z wysokością można pominąć.

RUCH CIECZY DOSKONAŁEJ

ბ ·u= 0 równanie ciągłości

równanie pędu:

równanie energii:

Pięć równań, cztery niewiadome ux, uy, uz, i p

Ale równanie energii można uzyskać jako iloczyn równania pędu i prędkości a więc równanie energii nie jest niezależne. Wystarczą zatem równanie ciągłości i trzy równania pędu.Zakładając, że pole prędkości jest bezwirowe, można jeszcze uprościć równania, bo istnieje wtedy potencjał prędkości taki, że

ბ 2ၪ = 0, który spełnia równanie Laplace'a.

Bo jeśli u = ၪბ, to po podstawieniu do równania ciągłości otrzymamy powyższe równanie tj. laplasjan.

Zagadnienie wyznaczenia przepływu cieczy doskonałej dla ruchu bezwirowego to najpierw wyznaczenie potencjału prędkości jako rozwiązania równania Laplace'a z odpowiednimi warunkami brzegowymi dotyczącymi wartości pochodnych potencjału prędkości, zaś później wyznacza się ciśnienie.

Ciśnienie wyznacza się albo z równania pędu albo z równania energii.

Jeśli zatem w przepływie istnieje potencjał sił masowych jednostkowych V, to ciśnienie można wyznaczyć z całek równania Eulera tzn. całki Cauchy'ego i Lagrange'a

Cauchy - Lagrange:

Bernoulliego:

W przypadku ruchu jednowymiarowego będziemy się opierać na równaniu Bernoulliego i na całkowej formie równania ciągłości

u S = const

u - prędkość średnia

S - pole powierzchni przepływu

POTENCJAŁ PRZYSPIESZEŃ

Gdy pole sił jednostkowych jest potencjalne, to

gdzie

- potencjał przyspieszeń

Zatem gdy istnieje potencjał V, to przepływ można rozwiązać rozwiązując równanie ბ2p = 0 (równanie Laplace'a względem p) z warunkami brzegowymi na p (zagadnienie Dirichleta), dalej wyznaczamy pole przyspieszeń a następnie pole prędkości

 Zagadnienia przepływu cieczy doskonałej

ႮTeoria potencjału

Zastosowania całki Bernoulliego i zasady zachowania pędu

Przepływ stacjonarny jednowymiarowy

Parametry przepływu można określić na podstawie równania ciągłości i równania Bernoulli'ego.

Niech potencjał pola V = - g z , wtedy równanie Bernoulli'ego

Ruch cieczy w jednorodnym polu grawitacyjnym.

WYPŁYW CIECZY PRZEZ MAŁY OTWÓR

Obliczmy prędkość cieczy wypływającej z otworu

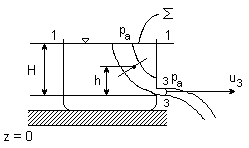
H = const ruch stacjonarny

S = const - przekrój otworu wylotowego

H - środek ciężkości przekroju otworu

pa - ciśnienie atmosferyczne

ၓ - pole lustra wody

l - wymiar liniowy otworu

 S << ၓ, H >> l

Porównując wartości energii w przekroju 1 - 1 i 3 - 3 otrzymamy

Ponieważ: p1 = p3 = pc

 z1 = z0 + H z3 = z0

u1 << u3 bo S << ၓ

 oraz u1 S1 = u3 S3

 Podstawiając otrzymamy:

wzór Torricellego

 Prędkość wypływu przez mały otwór zależy tylko od wysokości H nazywanej wysokością naporu.

Ogólniejszy przypadek wypływu przez mały otwór

H' = const

H'' = const

p' = const

p'' = const

S << ၓ', S <<ၓ''

 Poziom zerowy na wysokości otworu

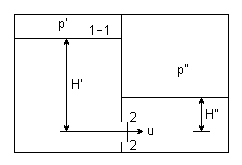
u^'=0 wtedy ρ^' - wypływa do przestrzeni z ρ^''

WYPŁYW PRZEZ DUŻY OTWÓR

Wysokość otworu a tego samego rzędu co wysokość naporu H, H=const

Obliczyć wydatek Q cieczy przez duży prostokątny otwór aთ b w pionowej ścianie zbiiornika, H = const, przepływ ustalony, przekrój otworu wielokrotnie mniejszy od poziomego przekroju zbiornika,

Stosując wzór Torricellego:

Wydatek cieczy Q

Prosty wzór, bo założono jednowymiarowy wypływ, takie założenie zastosowano do zagadnienia, które jest w gruncie rzeczy trójwymiarowe

WYPŁYW QUASI - STACJONARNY

ၳ0- przekrój otworu w dnie naczynia

ၳ (z) - przekrój poziomy funkcją z (wysokości)

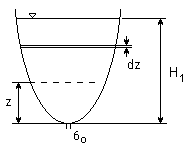
Zbiornik o dowolnym kształcie. Poziom wody opada, obliczmy czas, w jakim ciecz opadnie od H1 do H2. Zagadnienie jest w zasadzie niestacjonarne, zasadniczo nie powinno się stosować do jego rozwiązania równania Bernoulli'ego.

Zastosujemy je jednak zakładając, że wzór Torricellego jest w przybliżeniu słuszny dla dowolnej chwili t pomiędzy 0 i T,

dla dowolnego położenia zwierciadła pomiędzy H1 i H2.

Chwilowy wydatek cieczy:

Jeśli założyć, że poziom cieczy obniży się o dz w czasie dt, to można obliczyć ile cieczy wypłynie ze zbiornika

dla ၳ (z) = const = ၳ,

i dla H₂ = 0

Dla zbiornika kulistego o promieniu R

dla kuli

ostatecznie

RÓWNOWAGA WZGLĘDNA cieczy w ruchu postępowym jednostajnie przyspieszonym

Ciecz idealna o gęstości ၲ wypełnia zbiornik do wysokości h, porusza się wraz ze zbiornikiem ruchem postępowym jednostajnie przyspieszonym au Płaszczyzna Oxy pokrywa się z dnem naczynia. Ruch odbywa się w płaszczyźnie Oyz.

 Przyspieszenie au tworzy kąt ၢ z osią Oy.

 Na każdy element płynu działa siła jednostkowa względna

Fw = g - au, , a jej rzuty to: x = 0,

y = - acos ၢ, z = - g - asin ၢ, a - moduł a_u

Równania równowagi względnej:

i różniczka zupełna

Po scałkowaniu

p = -ၲ [a y cosၢ + (a sinၢ + g) z] + c1 (*)

stała c1 - z warunku na ciśnienie na powierzchni swobodnej

W punkcie M1 na powierzchni swobodnej i w jednym pionie z punktem M o współrzędnych (y, z + t )

pa = - ၲ [a y cosၢ + (a sinၢ + g)(z + t)] + c1

skąd

c1 = pa + ၲ [a y cosၢ + (a sinၢ + g)(z + t)]

 i po podstawieniu do równania (*) mamy

 p = pa + ၲ(g + a sinၢ) t

Z tego równania otrzymujemy równanie powierzchni izobarycznych

Jest to równanie płaszczyzn równoległych nachylonych do poziomu pod kątem ၡ

RÓWNOWAGA WZGLĘDNA płynu nieściśliwego w ruchu jednostajnie obrotowym wokół stałej osi

Fw = g + ၷ r 2

i składowe Fwr = ၷ 2r

Fw၊ = 0

Fwz = - g

 Podstawiając do równań Eulera we współrzędnych cylindrycznych

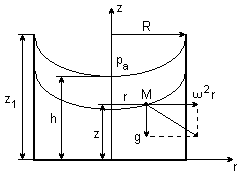
i znowu tworzymy różniczkę zupełną:

i po scałkowaniu

WYPŁYW Z NACZYNIA WIRUJĄCEGO

Niejednorodne pole sił masowych jednostkowych.  

Mały otwór w ściance zbiornika wirującego z prędkością ၷ kątową względem osi zbiornika. Otwór znajduje się w odległości H od najniższego punktu zwierciadła cieczy.Przyjmujemy układ odniesienia wirujący ze zbiornikiem, początek układu na wysokości otworu.

Potencjał dla takiego (przepływu) ruchu cieczy

a równanie Bernoulli'ego

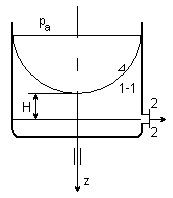
Stosując to równanie dla najniższego przekroju lustra cieczy 1 - 1 i dla przekroju 2 - 2 otrzymamy

vz - prędkość względem wirującego zbiornika

ZJAWISKA TOWARZYSZĄCE WYPŁYWOWI CIECZY

Eksperyment Ⴎ przekrój strumienia cieczy w pewnej odległości od otworu jest mniejszy od przekroju samego otworu.

Zjawisko to nosi nazwę kontrakcji strumienia .

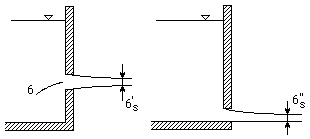
współczynnik kontrakcji

Obliczone teoretycznie wsp. kontrakcji dla otworu kołowego i dla nieskończenie dla długiej szczeliny

Ponadto różnice prędkości średniej teoretycznej i eksperymentalnej vr < vt zjawisko straty prędkości przy wypływie

Wtedy

współczynnik prędkości, Kontrakcja - przyczyna: siły bezwładności

Strata prędkości - przyczyna: lepkość cieczy Rzeczywisty wydatek: Q r = ၳၡ თ ၢ vt = ၡ ၳၢ vt = ၡ ၢ Q tၡ ၢ - współczynnik wydatku

PRZYSTAWKI

Aby uzyskać spoistą strukturę strumienia cieczy, krótkie rury stanowiące obramowanie otworu wypływowego

Opis przepływu Ⴎ równania Bernoulli'ego + ciągłości

Rodzaje przystawek: walcowe, stożkowe, kształty specjalne

v1 > v2

p1 < p2 = pa

Stożkowa zbieżna - prądownica strażacka

Stożkowa rozbieżna - rura ssąca

Przystawka rozbieżna - przepływ

 Zbiornik otwarty, H = const

Równania Bernoulli'ego dla przekrojów 0 - 0, 1 - 1, 2 - 2

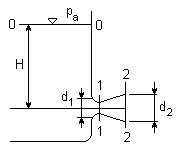
prędkość na wylocie przystawki

Równanie ciagłości

Wydatek

Ciśnienie w minimalnym przekroju przystawki

Podstawiając do równania Bernoulli'ego

W przekroju minimalnym przystawki ciśnienie jest niższe od atmosferycznego, prędkość jest większa od tej, jaka ustaliłaby się gdyby przystawki nie było.Ze wzrostem prędkości łączy się wzrost wydatku, uzasadniona jest więc nazwa rura ssąca.

Analiza wzoru na ciśnienie:

Ciśnienie p może przybrać dowolnie małą a nawet ujemną wartość, zależy tylko od wysokości naporu H, stosunku średnic d2/d1 i ciśnienia atmosferycznego. W rzeczywistości: nie spada dowolnie nisko, bowiem ciecz zaczyna wrzeć z chwilą, gdy ciśnienie statyczne p2 zrówna się z ciśnieniem wrzenia cieczy odpowiadającego naturalnej temperaturze cieczy. Najniższe ciśnienie jakie może wystąpić w przepływającej cieczy jest równe ciśnieniu wrzenia odpowiadającego temperaturze cieczy.Kawitacja: zespół zjawisk towarzyszących lokalnemu spadkowi ciśnienia cieczy do ciśnienia wrzenia.

KAWITACJA

Złożone zjawisko przepływowe

  Pęcherzyki pary lub gazu rozpuszczonego w cieczy szybko zanikają po przesunięciu do strefy podwyższonego ciśnienia. Kolaps pęcherzyka (zaniknięcie) niebezpieczny w przypadku wystąpienia przy ściance, gdyż związany z mikrouderzeniem. Związany z tym jest dźwięk, hałas, oraz niszczenie ścianki: tzw. korozja kawitacyjna, mikropęknięcia i utlenianie tlenem zawartym w cieczy oraz przepłukiwanie mikropęknięć, ogólnie: niszczenie materiału.

  Ponadto z kawitacją związana jest strata energii cieczy, tzw. kawitacyjna strata ciśnienia związana z nieodwracalnymi przemianami energii występującymi podczas parowania i skraplania cieczy lub wydzielania się gazu i ponownego rozpuszczania w cieczy.

Przeciwdziałanie: niedopuszczanie do kawitacji.

 pmin > pw

Sposoby niedopuszczenia do kawitacji:

1) kształt urządzenia hydraulicznego taki, aby nie obniżyć ciśnienia do ciśnienia wrzenia

2) podwyższenie ciśnienia statycznego

3) zmniejszyć ciśnienie wrzenia przez obniżenie temperatury cieczy

Współczynnik kawitacji: (liczba kawitacji)

Przykład: określić stosunek średnic rury ssącej, aby w rurze nie wystąpiła kawitacja:

tw = 20oC, p = 1 bar, H1 = 1 m, H2 = 3m, pw = 0,02378 bara

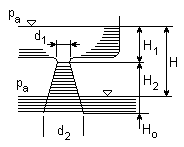
p2 > pw

Jest to jednak warunek na prędkość średnią, w oparciu o lokalne warunki prędkości,

która może być wyższa od wartości średniej. Może wystąpić kawitacja. Stąd jednowymiarowa analiza przepływu może być niewystarczająca, gdyż pomimo spełnienia powyższego warunku może wystąpić kawitacja.

POMIAR PRĘDKOŚCI LOKALNEJ W STRUMIENIU PŁYNU

 Na podstawie równania Bernoulli'ego

Ponieważ z = 0 (można założyć)

- ciśnienie całkowite (spiętrzenia, gdy v = 0)

Wyznaczenie prędkości płynu

-pomiar ciśnienia całkowitego - rurka Pitota, rurka Prandtla

-pomiar ciśnienia statycznego - zwężki, kryzy, ...

Rurka (sonda) Pitota

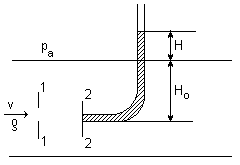
p2 = pa + ၲ g(H + H0) w przekroju 2 - 2

i po podstawieniu

Zanurzenie Ho nie wchodzi do wyniku

Rurka Pitota przyłączona do U - rurki (manometru)

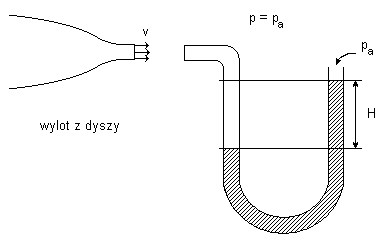
Dla sondy Pitota trzeba oddzielnie mierzyć ciśnienie statyczne, lub znać skądinąd jego wartość. Dla pomiaru w strumieniu powietrza pomijamy jego ściśliwość, co można zrobić dla v <100 m/s lub Ma<0,3.

Rurka (sonda) Prandtla (sonda statyczna Pitota)

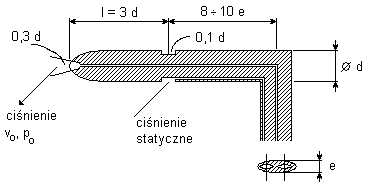
Sonda Prandtla- służy do jednoczesnego pomiaru cisnienia całkowitego i statycznego

Jednoczesny pomiar ciśnienia całkowitego (spiętrzenia) i ciśnienia statycznego.

-         otwór na wlocie do pomiaru ciśnienia całkowitego

-         otwory na bocznej ściance sondy do pomiaru ciśnienia statycznego

Manometr podłączony do rurki Prandtla wskaże ciśnienie dynamiczne

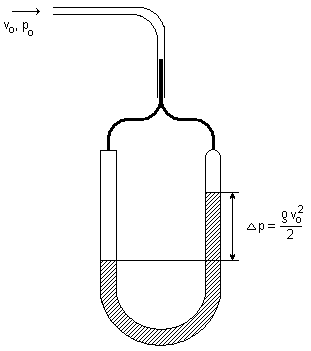
Sonda Prandtla- tak jak sonda Pitota mierzy lokalną prędkość przepływu.

ZWĘŻKA VENTURIEGO

Pomiar prędkości lokalnej w strumieniu płynu

Zwężka Venturiego (do pomiaru prędkości lokalnej)

Zwężka zbieżno-rozbieżna

C - stała zależna od konstrukcji zwężki

Gdzie

Może być v1 < vo i ciśnienie w otworkach O różne od ciśnienia po

Dlatego

Zwężkę Venturiego możemy stosować do niższych prędkości, gdy sonda Prandtla nie wytwarza odpowiednio dużej różnicy ciśnień.

Pomiar wydatku i prędkości średniej

-na podstawie pomiaru rozkładu prędkości lokalnej zmierzonej wg podanych powyżej metod, tj.

v = v(x, y), ,

Metoda pracochłonna, żmudna, stosowana rzadko.

 -zwężki miernicze (pomiarowe). Kryzy, dysze, zwężki Venturiego wbudowane w przewód na stałe.

Metoda oparta na równaniu Bernoulliego i jest w zasadzie identyczna do pomiaru przy pomocy zwężki Venturiego tj. pomiaru różnicy ciśnień ၄p = p1 - p2 przed i za zwężką.

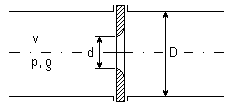
Kryza pomiarowa

D - minimalna średnica zwężki

ၡ - współczynnik wydatku

ၥ - współczynnik ściśliwości płynu

၄ps - straty ciśnienia statycznego

ၡ, ၥ - współczynniki poprawkowe

- moduł zwężki (współczynnik rozwarcia)

ZASTOSOWANIE ZASADY ZACHOWANIA PĘDU I MOMENTU PĘDU.

Reakcja wywierana przez swobodny strumień cieczy doskonałej

na powierzchnię ciała stałego.

Wzory całkowe zasady zachowania pędu i momentu pędu.

Stosować tylko wtedy, gdy ruch płynu jest ustalony.

Przeszkoda nieruchoma. Strumień płynu o żądanej gęstości ၲ porusza się wzdłuż nieruchomej ścianki zmieniającej jego kierunek o kąt ၡ.

Wyznaczyć reakcję R wywieraną przez ciecz na ściankę.

Założenia:

Ruch odbywa się w płaszczyźnie rysunku, ၭ = 0, F = 0, (czyli pominąć tarcie i siły masowe) ponadto pa = const czyli na zewnątrz strumienia panuje stałe ciśnienia pa.

Bilans pędu na powierzchniach kontrolnych

Pierwsza i druga całka:

Trzecia, czwarta, piąta, szósta, siódma i ósma całka = 0.

---