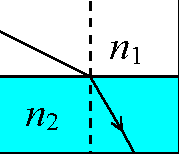
Prawo załamania światła Zmiana kierunku promieni świetlnych podczas załamania nie jest przypadkowa. Opisuje to prawo załamania światła nazywane niekiedy prawem Snelliusa (patrz - biografie: Snell van Royen). Prawo załamania światła łączy ze sobą dwa kąty - kąt padania na powierzchnię rozgraniczającą dwa ośrodki i kąt załamania powstający gdy promień przejdzie granicę i zacznie się rozchodzić w drugim ośrodku (patrz rysunek niżej).

Warto zwrócić uwagę na fakt, że kąty padania i załamania są liczone od normalnej do powierzchni, a nie od samej powierzchni. (Więcej informacji na temat liczenia kątów od normalnej znajduje się w rozdziale Kąty padania, odbicia, załamania)

Prawo załamania - postać 1 - podstawowa
		α - kąt padania β - kąt załamania v1 - prędkość światła w ośrodku 1 v2 - prędkość światła w ośrodku 2
Słownie prawo załamania można sformułować następująco: Stosunek sinusa kąta padania, do sinusa kąta załamania jest dla danych ośrodków stały i równy stosunkowi prędkości fali w ośrodku pierwszym, do prędkości fali w ośrodku drugim. Kąty padania i załamania leżą w tej samej płaszczyźnie. Inne postacie prawa załamania Zdefiniujmy wielkość zwaną bezwzględnym współczynnikiem załamania ośrodka:
	v - prędkość światła w ośrodku c - prędkość światła w próżni (c = 299 792 458 m/s) n - bezwzględny współczynnik załamania
Podstawmy teraz tę wielkość do wzoru na prawo załamania, zmieniając nieco postać - tzn. wyliczając prędkość v (wzór otrzymujemy mnożąc obie strony ostatniego równania przez v i dzieląc przez n):
Podstawimy ten wzór raz w wersji dla ośrodka 1  (n1 - bezwzględny współczynnik załamania w ośrodku 1)   A potem w wersji dla ośrodka 2  (n2 - bezwzględny współczynnik załamania w ośrodku 2)

Wtedy otrzymamy:
		n1 - bezwzględny współczynnik załamania ośrodka 1 n2 - bezwzględny współczynnik załamania ośrodka 2 c - prędkość światła w próżni
Stąd ostatecznie będziemy mieli drugą postać prawa załamania światła. Wzór prawa załamania - postać 2   Ta wersja prawa załamania wiąże kąty padania i załamania z bezwzględnymi współczynnikami załamania w obu ośrodkach. Sformułowanie słowne: Stosunek sinusa kąta padania, do sinusa kąta załamania jest równy stosunkowi bezwzględnego współczynnika załamania ośrodka do którego przechodzi fala, do bezwzględnego współczynnika załamania ośrodka, z którego fala pada na powierzchnię rozgraniczającą oba ośrodki. Wzór prawa załamania - postać 3 Jest jeszcze trzecia postać prawa załamania. Powstaje ona po zdefiniowaniu kolejnej wielkości zwanej względnym współczynnikiem załamania:
		n1 - bezwzględny współczynnik załamania ośrodka 1 n2 - bezwzględny współczynnik załamania ośrodka 2 n12 - współczynnik załamania (względny) ośrodka 2 względem ośrodka 1
Warto zwrócić uwagę na fakt, że względny współczynnik załamania czyta się od tyłu: - jest to współczynnik załamania ośrodka drugiego (do którego wchodzi światło) względem ośrodka pierwszego (z którego przychodzi światło). Po podstawieniu względnego współczynnika załamania do 2 postaci prawa załamania otrzymamy: Zatem:   stosunek sinusa kąta padania do sinusa kąta załamania jest równy względnemu współczynnikowi załamania światła ośrodka do którego światło wpada względem ośrodka z którego światło wychodzi.

---