POLITECHNIKA ŚLĄSKA W GLIWICACH

WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA

Katedra Informatyki i Ekonometrii

Badania operacyjne

Projekt nr 1

Optymalizacja liniowa

Wykonał: Krystian Mrowiec

Data: 17.04.2008

Kierunek: ZiIP 2.2

Miasto: Zabrze

Funkcja celu: (a+8)x₁+ (b+10)x₂ min/max

Ograniczenia:

1. (2b+16)x₁+ (2c+18)x₂ ≤ 8a+8b+20

2. (a+4)x₁+ (b+6)x₂ ≤ 6(a+c+10)

3. (c+10)x₁+ (a+3)x₂≥ 2(b+c+2)

4. (a+c)x₁ ≤ (b+c+2)x₂

Po podstawieniu parametrów: a=6, b=4, c=2, otrzymuję następujący model, który traktuję jako model dualny

Fc: 14x₁+ 14x₂ max

Ograniczenia:

24x1+ 22x2 ≤ 84 10x1+ 10x2 ≤ 108 12x1+ 9x2≥16 x1 ≤ 8x2 x1,x2≥0

0≤84-24x1-22x2 0≤108-10x1-10x2 0≤-16+12x1+9x2 0≤-8x1+8x2

Zadanie:

Producent opon Dębica produkuje opony do samochodów ciężarowych (x₁) i osobowych (x₂). Do produkcji tych opon wykorzystuje: kauczuk naturalny, guma i włókna szklane. Zużycie tych surowców na wyprodukowanie tysiąca opon, dopuszczalne limity zużycie surowców oraz zyski ze sprzedaży podaje tabela:

Wyrób	Zużycie surowców do produkcji opon			Zysk jednostkowy
		Kauczuk naturalny	Guma		Włókna szklane
Opony do samochodów ciężarowych	24	10	12	14
Opony do samochodów osobowych	22	10	9	14
Dobowy limit zużycia surowców	84	108	16

Ile należy wyprodukować opon do samochodów osobowych, a ile do samochodów ciężarowych, aby nie przekraczając limitów zużycia surowców zmaksymalizować zysk ze sprzedaży.

Ponadto należy uwzględnić warunek, że opony do samochodów ciężarowych powinno się produkować nie więcej niż opon do samochodów osobowych.

Rozwiązanie metodą graficzną:

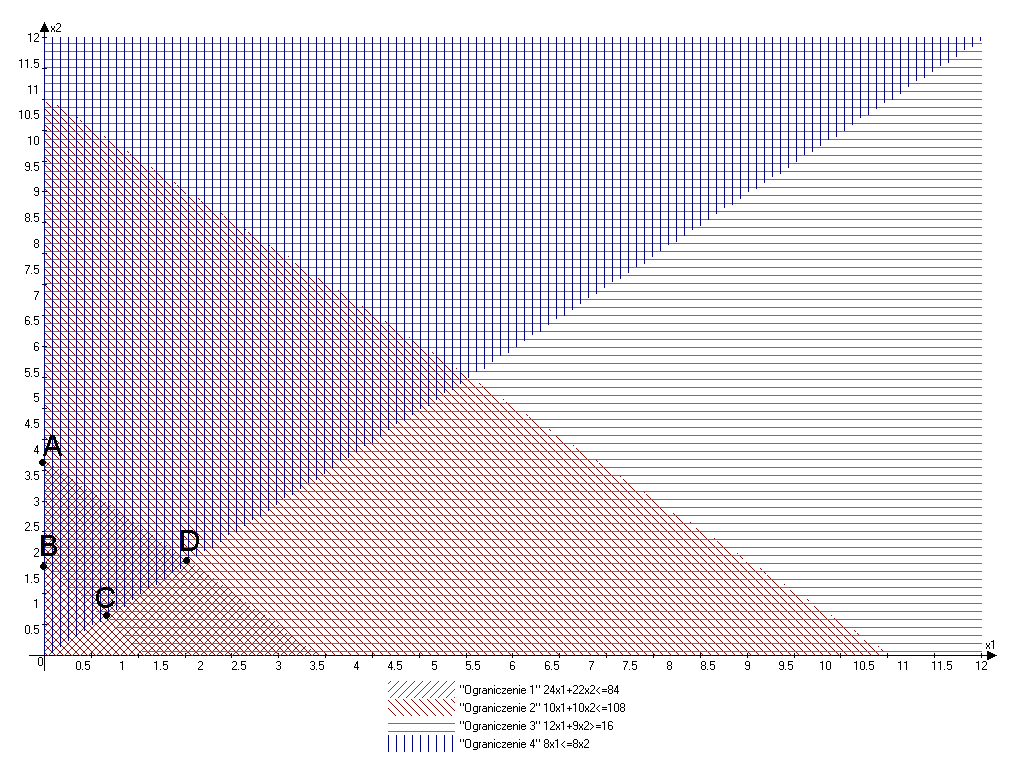
Obliczam współrzędne punktu A Stąd współrzędne punktu	Obliczam współrzędne punktu B Stąd współrzędne punktu
Obliczam współrzędne punktu C Stąd współrzędne punktu	Obliczam współrzędne punktu D Stąd współrzędne punktu

Podstawiam otrzymane wartości x₁ i x₂ do funkcji celu, aby znaleźć optymalne rozwiązania:

1. 
   

Fc_A:
MAX

2. 
   

Fc_B:

3. 
   

Fc_C:

4. 
   

Fc_D:

Na tej podstawie nasze optymalne rozwiązanie (maksymalizujące zysk) to: zaprzestanie produkcji opon do samochodów ciężarowych, a wyprodukowanie 3820 sztuk opon przeznaczonych do samochodów osobowych, otrzymując zysk 53454 zł.

Model dualny

Funkcja celu modelu dualnego G: 84y₁+108y₂-16y₃+0y₄ min

Ograniczenia:

1. 24y₁+10y₂-12y₃+8y₄-14≥0

2. 22y₁+10y₂-9y₃-8y₄-14≥0

Podstawiam do równań wartość x₁ i x₂

1. y₁(84-24x₁-22x₂₎=0

2. y₂(108-10x₁-10x₂)=0

3. y₃(-16+12x₁+9x₂)=0

4. y₄(-8x₁+8x₂)=0

5. x₁(24y₁+10y₂-12y₃+8y₄-14)=0 x₁=0 y₁≥0

6. x₂(22y₁+10y₂-9y₃-8y₄-14)=0

Podstawiam otrzymane wyniki do funkcji celu modelu dualnego:

G:

Rozwiązanie modelu liniowego za pomocą programu Excel (dodatek Solver)

Rozwiązanie modelu dualnego za pomocą programu Excel (dodatek Solver)

Odpowiedź:

W celu zmaksymalizowania zysków, producent opon Dębica powinien w ciągu doby produkować 3820 opon do samochodów osobowych, natomiast całkowicie zaprzestać produkcji opon do samochodów ciężarowych. W ten sposób wypracuje 53454 zł zysku.

str. 2

---