36. Ogólna charakterystyka modelu wzrostu Harroda.

I=O (C+I=C+S), przyjmujemy ze S=O

I/Y=O/Y

ΔY/Y * I/ΔY = O/Y

ΔY/Y = O/Y : I/ΔY = r

Gdzie:

ΔY/Y = r - tempo wzrostu dochodu narodowego

O/Y = s - udział oszczędności w dochodzie narodowym, wyraża stałą, przeciętna i krańcową skłonność do oszczędzania; stopa oszczędności

I/ΔY = k - krańcowy współczynnik kapitałochłonności produkcji mierzony wielkością nakładu inwestycyjnego I na jednostkę dochodu narodowego ΔY; stopa kapitałochłonności

Równanie Harrod zapisał w postaci:

r = s/k = Gf

Jest pierwszym modelem ujmującym gospodarkę w sposób dynamiczny. Gf to faktyczna stopa wzrostu, której niezbędnym uzupełnieniem są gwarantowana stopa wzrostu (Gw) oraz naturalna stopa wzrostu (Gn).

Gw - wyraża sytuację wzrostu gosp. przy pełnym wykorzystaniu zdolności prod.

Gn - wyraża potencjalne możliwości rozwoju, a składają się na nią stopa przyrostu naturalnego β (ilość przyszłej siły roboczej) +postęp tech. α (przyrost wydajności pracy)

Wyróżnił 3 stany:

1. Gw=Gf=Gn - stan równowagi dynamicznej, gospodarka wytwarza tyle ile może wchłonąć popyt jednocześnie rezerwy zasobu ludzkiego dokładnie pokrywają zapotrzebowanie.

2. Gw>Gf<Gn - mechanizm depresyjny, agregatowa podaż zaczyna przewyższać regatowy popyt, co prowadzi do powstania zapasów. Przedsiębiorstwa ograniczają produkcje i zwalniają pracowników. Jednocześnie spada stopa inwestycji indukowanych (zależnych od dochodu narodowego), a inwestycje autonomiczne (wnikające z postępu technicznego) od dochodu stanowią dolną granicę spadku dla PKB.

3. Gw<Gf<Gn - Sytuacja nie wykorzystanych zdolności produkcyjnych przedsiębiorstwa inwestują gdyż wysoka jest stopa oszczędności. Agregatowy popyt stale przewyższa podaż co pobudza nowe inwestycje i i dalszy wzrost zatrudnienia, popytu i PKB.

Według Harroda wzrost zrównoważony jest wprost proporcjonalny do stopy inwestycji, a odwrotnie proporcjonalny do kapitałochłonności inwestycji. Postuluje by stosować kapitałoooszczędne inwestycje, co daje efekt w postaci niższego kosztu wytworzenia jednostki dochodu narodowego.

37. Sposób ujęcia przez Domara popytowego i podażowego aspektu wydatków inwestycyjnych.

Podejście Domara polega na zauważeniu dualnego charakteru inwestycji. Po pierwsze inwestycje wpływają na wzrost możliwości produkcyjnych czyli aparatu wytwórczego, po drugie zaś kreują możliwości konsumpcyjne czyli korzystnie oddziałują na stronę popytową gospodarki. Autor przyjął założenia wyjściowe do modelu:

1. stała skłonność do oszczędzania α

2. stała produktywność inwestycji γ

3. pełne zatrudnienie i wykorzystanie zdolności produkcyjnych

4. nie uwzględnia handlu zagr. oraz wydatków rządowych

Przy danych założenia przyrost zdolności produkcji = przyrostowi PKB

Strona potażowa inwestycji:

Strona popytowa:

Porównując ze sobą otrzymamy:

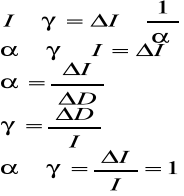
Warunek zrównoważonego rozwoju

Jeżeli rzeczywista stopa wzrostu inwestycji r jest większa niż iloczyn γ*α to zagregowany popyt rośnie szybciej niż możliwości produkcyjne i gospodarce grozi niedobór możliwości produkcyjnych. Po pewnym czasie ten niedobór może stać się przyczyną do dalszego wzrostu inwestycji. Jeśli natomiast rzeczywista stopa wzrostu inwestycji jest mniejsza niż iloczyn γ*α to zagregowany popyt rośnie wolniej niż możliwości produkcyjne i gospodarce grozi nadwyżka możliwości produkcyjnych. Aby uniknąć niedoborów i nadwyżek mocy produkcyjnych trzeba przeznaczyć konkretną wielkość na inwestycje w danym okresie i będzie ona przebiegała wzdłuż linii wyznaczonej przez γ*α. W takim wypadku gospodarka znajdzie się w równowadze.

38. Rola mnożnika inwestycyjnego we wzroście gospodarczym.

Mnożnik Keynesa wyprowadzenie:

D=I+C : dochód = suma inwestycji i konsumpcji

: dochód = suma stopy inwestowania i akumulacji

;

;

produktywność inwestycji (krańcowa) :
;

Przyrost dochodu wywołany przyrostem nakładu inwestycji o jednostkę jest tym większy im wyższa jest krańcowa stopa konsumpcji :
a mniejsza stopa oszczędzania.

krańcowa produktywność inwestycji (przyrost dochodu wywołany ostatnią jednostką poniesionych nakładów). Rola mnożnika polega na „mnożeniu” produktywności inwestycji, co oznacza, że każda kolejna inwestycja daje bardziej niż proporcjonalne przyrosty dochodu narodowego. Dzieje się tak dlatego, że każda inwestycja uruchamia złożoną liczbę procesów gospodarce: Popyt na środki prod. , siłę roboczą, nowe technologie, nowe usługi, itd. Jedna inwestycja ma więc przełożenie na wiele dziedzin.

39. Równanie Michała Kaleckiego jako przykład podażowego modelu wzrostu gospodarczego.

Kalecki opracował model wzrostu dla gospodarki centralnie zarządzanej w warunkach dostępności zarówno środków produkcji jak i siły roboczej. Model opiera się na tezie, że tempo wzrostu jest wprost proporcjonalne do inwestycji i odwrotnie proporcjonalne do ich kapitałochłonności. Model:

I/D - stopa inwestycji w roku t-1

1/k - produktywność danych nakładów inwestycyjnych, odwrotność kapitałochłonności

a - zużycie fizyczne (amortyzacja) i moralne sprzętu produkcyjnego odejmowane od dochodu jako koszt

u - usprawnienia produkcyjne organizacyjne itd.

s - koszty alternatywne nakładów na inwestycje

n - dochody z tytułu zmianowego wykorzystania czynników wytwórczych

40. Funkcja Cobba-Douglasa jako przykład wieloczynnikowego modelu wzrostu gospodarczego.

Cobb i Douglas opracowali funkcję będącą wieloczynnikowym modelem wzrostu. W

wyjściowej postaci zmiennymi są: F - wielkość majątku trwałego , L - liczba zatrudnionych, Z - czynnik ziemi (pomijany jednak w dalszej analizie jako, że uznano ten zasób jako stały - z czym na pewno nie zgadza się Czyżewski).

Postać matematyczna i warunki na parametry:

Y - dochód narodowy w czasie t=1,2,3,4,...,n lat,

F - wielkość majątku trwałego w gospodarce narodowej w latach t,

L - liczba zatrudnionych przy wytwarzaniu dochodu narodowego w czasie t,

a, ε - parametry stałe

a - czynnik skalujący

- właściwością tej funkcji jest to, że wykładniki jej sumują się do 1

ε + (1 - ε) = 1

- czyli opiera się na założeniu stałych korzyści ze skali produkcji.

Szacowana wartość parametru ε wyraża udział majątku trwałego trwałego tworzeniu

dochodu narodowego, a parametr 1 - ε wyraża udział zatrudnienia w tworzeniu dochodu

narodowego.

Funkcja ma sens ekonomiczny gdy 0 < ε < 1

Równanie tempa wzrostu dochodu narodowego - różniczka funkcji

Funkcja ta dowodzi, że nie da się tempa wzrostu opisać jedynie jako zależności między F_t (majątkiem) a Z_t (zatrudnieniem), a trzeba uwzględnić tzw. „czynnik resztkowy” γ spowodowany postępem i innowacjami. Późniejsze badania dokonywane nad zależnościami ukazanymi w tej funkcji dowiodły, że coraz większy wpływ na wzrost mają postęp naukowy i wynalazki.

41. Istota poprawki J. Tinbergena w modelu Cobba-Douglasa.

AD.6

Istota poprawki Tinbergena w funkcji Cobba- Douglasa sprowadza się do tego, że T. zauważył, iż nie można sprowadzać wzrostu dochodu tylko do rosnących wartości majątku oraz zatrudnienia, ponieważ ich efekty relatywnie spadają z okresu na okres na rzecz rosnących korzyści z tytułu postępu innowacyjnego. Doło…żył więc do funkcji współczynnik v oznaczający właśnie ten postęp.

e - podstawa logarytmu naturalnego

v - stopa wzrostu dochodu narodowego wynikająca z postępu innowacyjnego

t - kolejne lata objęte analizą

Założenia:

- wykładniki nie muszą zrównać się do 1,

- Wprowadzony osobny, niezależny parametr, uchyla również założenie o stałych

korzyściach ze skali produkcji.

Mamy więc:

42. Interpretacja współczynników „e” i „a” w funkcji Cobba-Douglasa.

AD.7

Parametr „a” jest czynnikiem skalującym wartości modelu (ustawiającym model)

Parametr „ε” (nie jak napisała szanowna Joanna „e”) jest w równaniu wzrostu dochodu narodowego współczynnikiem udziału (wagą udziału) majątku i ztrudnienia w tworzeniu dochodu narodowego.

Parametr „ε” po przekształceniach:

Dzieląc funkcję przez L

Różniczkując powyższe równanie

Parametr ε jest zatem współczynnikiem elastyczności tempa wzrostu produkcyjności

pracy do tempa wzrostu technicznego uzbrojenia pracy.

Zatem gdy ε Є (0,1) oznacza, że stopa wzrostu technicznego uzbrojenia pracy przewyższa

stopę wzrostu wydajności pracy

Dochód więc reaguje wolniejszym wzrostem na wzrost wielkości majątku trwałego F

Jeżeli F↑ o 1% to Y↑ o ε · Y

Jeżeli L↑ o 1% to Y↑ o (1 - ε) ·Y

---