Łódź, dn. 25 listopada 2002 r.

Wydział Chemiczny.

Kierunek

Papiernictwo i Poligrafia.

Ćwiczenie Nr 99

Oznaczanie współczynnika dyfuzji elektrolitu metodą komorową.

Ćwiczenie wykonano:25.11.2002 r.

Sprawozdanie złożono: 2.12.2002 r.

Ćwiczenie wykonała:

Agnieszka Andruszkiewicz

Część teoretyczna.

Dyfuzją nazywamy samorzutny proces przenoszenia cząsteczek jednej substancji względem drugiej substancji wywołany gradientem potencjałów chemicznych składników. Pierwsze prawo Ficka stwierdza, że przepływ cząsteczek jest proporcjonalny do gradientu stężenia;

J = - D

Przepływ J podaje liczbę cząsteczek przechodzących w jednostkowym czasie przez w jednostkową powierzchnię przekroju prostopadłego do kierunku gradientu stężenia ( x),

jest liczbą cząsteczek w jednostkowej objętości w rozpatrywanym punkcje,

D nazywamy współczynnikiem dyfuzji, zależy od rodzaju układu, (w którym zachodzi proces), od temperatury, stężenia, a czasem od ciśnienia. Znak ,,-,, oznacza, że przepływ jest w stronę malejącego stężenia. Prędkość dyfuzji jest wprost proporcjonalna od różnicy stężeń i odwrotnie proporcjonalna do grubości warstwy, przez którą proces zachodzi.

. W roztworach rozcieńczonych gradient potencjału chemicznego składnika może zostać zastąpiony gradientem stężenia, a przepływ składnika wywołany dyfuzją możemy zapisać;

J_i = -D grad c_i

Przepływ składnika J_i powoduje zmiany jego stężenia w czasie, które opisuje II prawo FICKA

=
( D
)

Celem mojego ćwiczenia jest oznaczenie współczynnika dyfuzji elektrolitu metodą komorową. Współczynnik dyfuzji D wyznaczę eksperymentalnie rozwiązując II prawo FICKA dla odpowiednich warunków brzegowych i początkowych. W szczególnym przypadku, gdy przepływ jest stacjonarny, niezmienny w czasie, współczynnik dyfuzji D można wyznaczyć z praw FICKA . Metody wyznaczenia wartości D opartej na rozwiązaniu I prawa FICKA nazywa się metodami stacjonarnymi i należy do niej moja metoda, którą będą wykorzystywała do realizacji ćwiczenia a jest nią metoda komorowa.

Opis metody komorowej.

Komora dyfuzyjna składa się z dwóch części o objętościach V₁ i V₁₁, rozdzieloną przegrodą porowatą (diafragmą), którą stanowić może szkło porowate, błona polimerowa itp.W pierwszej komorze zawierającej elektrody umieszcza się elektrolit (np. chlorek potasu KCL) a w drugiej wodę destylowaną. Komorę podłącza się do konduktometru, na którym odczytujemy przewodnictwo elektrolitu. W wyniku dyfuzji przewodnictwo KCL powinno maleć.

Przegrodę porowatą charakteryzują dwa parametry;

A - efektywna powierzchnia

I - efektywna grubość

Rozwiązanie I prawa FICKA dla metody komorowej ma postać.

ln
=
D t

Gdzie
=
(
+
) jest wielkością charakterystyczną dla danej komory tzw. Stała komorowa wyrażona w cm^-2

Część doświadczalna.

1. Napełniam pierwszą komorę roztworem elektrolitu, natomiast do drugiej część komory nalewam wodą destylowaną.

2. Podłączam komorę do konduktometru i mierzę przewodnictwo w odstępach dziesięciominutowych przez 2-2,5 godz.

3. Ponieważ, mierzone przewodnictwo jest proporcjonalne od stężenia roztworu, wykonuję wykres zależności ln G = f (t).

4. Obliczam metodą najmniejszych kwadratów, współczynnik nachylenia prostej b

5. Obliczam współczynnik dyfuzji z wzoru b = -β D .

Po przekształceniu D =

Pomiary;

Pomiary wykonane w celu obliczenia współczynnika dyfuzji elektrolitu - metodą komorową.

Lp.	CZAS t	PRZEWODNICTWO G [mS]	ln G	t lnG	t
1	0	25	3,218875825	0	0
2	600	25	3,218875825	1931,325495	360000
3	1200	24,8	3,186352633	3823,62316	1440000
4	1800	24,2	3,186352633	5735,43474	3240000
5	2400	24,1	3,18221184	7637,308417	5760000
6	3000	23,5	3,157000421	9471,001263	9000000
7	3600	23	3,135494216	11287,77918	12960000
8	4200	22,8	3,126760536	13132,39425	17640000
9	4800	22,5	3,113515309	14944,87348	23040000
10	5400	22,45	3,111290614	16800,96932	29160000
11	6000	22,1	3,095577609	18573,46565	36000000

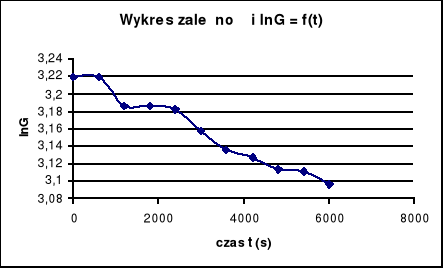
Równanie krzywej y = ax + b

y = -2,16855 ∗10^-5x + 3,22253

Natomiast współczynnik korelacji wynosi -0,986, jest bliski jedności, co świadczy o zależności liniowej.

Metodą najmniejszych kwadratów obliczam współczynnik nachylenia prostej, b wg wzoru

b =

gdzie;

m - liczba pomiarów

b = -2,16855 ∗10^-5

Wiedząc, że stała komory, wyznaczona metodą kalibracji dla 0,1 n KCl jest równa

β = 1,94 cm , można obliczyć współczynnik dyfuzji elektrolitu;

b = -β D

D =
=
= 1,1178*10^-5 [
]

Ponieważ współczynnik dyfuzji w roztworach ciekłych są rzędu 10^-4 - 10^-6,powyższy wynik mogę uznać za prawidłowy.

Wnioski;

Celem mojego ćwiczenia jest oznaczenie współczynnika dyfuzji. Obserwacja wykonywanego doświadczenia pokazuje Mi, że w wyniku procesu dyfuzji CHLORKU POTASU jego początkowe stężenie w komorze, w której został umieszczony, uległo zmniejszeniu. Ogólnie mówiąc nastąpiło przemieszczenie części jonów z komory z elektrodami do komory z wodą destylowaną.

Tym samym nastąpił spadek przewodnictwa właściwego, KCl, co jest zgodne z prawami chemii fizycznej elektrolitów, mówiącą o tym, że przy spadku stężenia roztworu obserwuje się spadek przewodnictwa właściwego i jednocześnie wzrasta przewodnictwo równoważnikowe.

Natomiast powolny spadek przewodnictwa chlorku potasu wynika z małej ruchliwości jonów K⁺ i Cl^-.

Omawiając wykres lnG = f(t) wykonany z otrzymanych wyników, mogą powiedzieć, że spadek przewodnictwa w kolejnych odstępach czasu jest coraz mniejszy. Świadczy to o tym, że dyfuzja jest coraz mniej intensywna i przebiega tylko do określonego momentu,do wyrównania stężeń jonów K⁺ i Cl^- w obu komorach.

5

---