Sprawozdania z analizy wybranych rozkładów statystycznych

1. Dane

1	2	3	4	5	6	7	8	9	10
360.9	422.9	283.8	318.0	283.4	580.9	572.1	414.1	413.9	315.9
11	12	13	14	15	16	17	18	19	20
434.3	423.2	468.4	617.6	421.5	656.7	542.7	251.6	667.9	438.6
21	22	23	24	25	26	27	28	29	30
452.6	385.5	321.2	413.0	341.8	543.3	463.6	469.9	424.3	686.6

2. Legenda do danych

Dane reprezentują liczbę godzin jaką na naukę poświęcają losowo wybrani studenci II roku INFORMTYKI studiów zaocznych.

3. Wnioski z testu błędów grubych

Badany wynik należy uznać za obciążony błędem grubym na poziomie istotności
,jeżeli spelniona jest nierówność.




Wynik taki należy wykluczyć z dalszej analizy i powtórzyć ją bez niego.

Dla mojego zestawu danych, dla poziomu istotności 0,05 nie ma wyniku obciążonego błędem grubym, ponieważ powyższa nierówność nie jest spełniona.

B4_minus=1,654

B4_plus=2,041

a wartość krytyczna b_i dla n=30 dla poziomu istotności
=0,05 wynosi 2,958

4. Wnioski z testu serii

Liczba serii może być miarą losowości badanego zjawiska. Zbyt mała świadczy o zakłóceniu losowości.

Liczba serii jest zmienną losową U, której wartości u spełniają zależność

2≤u≤n1+n2

gdzie:

n1- grupa wyrazów jednego rodzaju

n2- grupa wyrazów drugiego rodzaju

Hipotezę o niezależności wyników poszczególnych prób należy odrzucić, na poziomie istotności
jeżeli spelniona jest nierówność u≤U


Dla mojego zestawu danych, na poziomie istotności 0,05 hipotezę o niezależności wyników przyjmujemy, ponieważ powyższa nierówność nie jest spełniona:

Wartość krytyczna dla:

n1=y1=15

n2=y0=15

wynosi 11 a moja liczba serii wynosi 12

12≥11(U0,05)

5. Zestawienie parametrów rozkładów na podstawie oszacowania punktowego i graficznego

a) Rozkład normalny:

	Wartość oczekiwana - μ	Odchylenie średnie - σ
Oszacowanie punktowe	446,34	117,729
Oszacowanie graficzne	446,34	131,047

b) Rozkład logarytmonormalny:

	Wartość oczekiwana - μ	Odchylenie średnie - σ
Oszacowanie punktowe	446,995	120,475
Oszacowanie graficzne	450,407	134,429

c) Rozkład Gumbela:

	Miara rozrzutu zmiennej losowej - α	Moda - Mo
Oszacowanie punktowe	9,445⋅10^-3	503,108
Oszacowanie graficzne	9,035⋅10^-3	505,693

d) Rozkład Weibulla:

	Współczynnik kształtu - k	Parametr skali - Xm	Parametr przesunięcia - Xo
Oszacowanie punktowe	2,29	478,763	221,076
Oszacowanie graficzne	2,29	554,561	170,692

6. Zestawienie testów zgodności

Test Kołmogorowa-Smirnowa


Test w²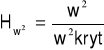


Test ω²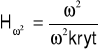


Hipoteza o zgodności rozkładów empirycznego z teoretycznym może być odrzucona lub nieodrzucona

	Test Kołmogorowa-Smirnowa	Test w^2	Test ω^2
Rozkład normalny	0,572 nieodrzucona	0,234 nieodrzucona	0,215 nieodrzucona
Rozkład log.-norm.	0,486 nieodrzucona	0,156 nieodrzucona	0,142 nieodrzucona
Rozkład Gumbela	0,805 nieodrzucona	0,528 nieodrzucona	0,488 nieodrzucona
Rozkład Weibulla	0,483 nieodrzucona	0,179 nieodrzucona	0,162 nieodrzucona

7. Zestawienie wyników uzyskanych w programie MOSTAT

	Rozkład normalny	Rozkład logarytmo-normalny	Rozkład Gumbela	Rozkład Weibulla
Wartość oczekiwana U50	441,97	432,03	-	-
Odchylenie średnie SIGMA	131,067	135,252	-	-
Wynik testu H	0,35224	0,22428	0,73075	0,24257
Miara rozrzutu zmiennej losowej - α	-	-	0,0075	-
Moda - Mo	-	-	502,7310	-
Parametr skali Xm	-	-	-	480.2711
Parametr skali X0	-	-	-	210.8830
K	-	-	-	1,9264

8. Wnioski (na podstawie 6 i 7)

Tabela zestawienia testów zgodności

Rozkłady	Dane z testów	Test K-S	Test w^2	Test ω^2	MOSTAT
Rozkład normalny	Wartość testowa	0,138	0,584	0,099	-
		Wartość krytyczna	0,2417	2,4933	0,4614	-
		Wynik testu H	0,572	0,234	0,215	0,35224
	Rozkład logarytmo-normalny	Wartość testowa	0,118	0,388	0,065	-
		Wartość krytyczna	0,2417	2,4933	0,4614	-
		Wynik testu H	0,486	0,156	0,142	0,22428
	Rozkład Gumbela	Wartość testowa	0,195	1,318	0,225	-
		Wartość krytyczna	0,2417	2,4933	0,4614	-
		Wynik testu H	0,805	0,528	0,488	0,73075
	Rozkład Weibulla	Wartość testowa	0,117	0,446	0,075	-
		Wartość krytyczna	0,2417	2,4933	0,4614	-
		Wynik testu H	0,483	0,179	0,162	0,24257

Z w/w tabeli wynika, że do analizy danych wejściowych możemy wybrać każdy z omawianych rozkładów:

- rozkład normalny

- rozkład logarytmo-normalny

- rozkład Gumbela

- rozkład Weibulla

Jednak jeżeli za kryterium przyjąć wyniki testów zgodności, najlepszy w tym przypadku jest rozkład logarytmo-normalny (alternatywnie najniższe wartości testów zgodności mamy w rozkładzie Weibulla.

4

---