W1
Prawdopodobieństwo - jest to miara zdarzenia losowego.
Zmienna losowa - jest to taka zmienna, która przybiera różne wartości liczbowe z określonymi prawdopodobieństwami.
Zmienna losowa jest skokowa (dyskretna) - jeżeli zbiór wartości, które może przyjmować zmienna jest skończony lub przeliczalny.
Zmienna losowa jest ciągła - jeżeli zbiór wartości, które może przyjmować zmienna jest nieprzeliczalny.
Dystrybuanta zmiennej losowej - jest to funkcja:
F(x) = P(X<x)
Rozkłady zmiennej losowej skokowej: +zero-jedynkowy; +dwumianowy; +Poissona.
W2
Estymator - jest to zmienna losowa o określonym rozkładzie. Jego podstawowe charakterystyki to wartość oczekiwana E(Tn) i odchylenie standardowe D(Tn).
Własności dobrego estymatora: +nieobciążoność; +zgodność; +wysoka efektywność.
Estymator jest asymptotycznie nieobciążony, gdy: lim b(Tn) = 0
Estymator jest zgodny, jeżeli: plim Tn = θ
Estymacja punktowa - polega na tym, że za ocenę parametru przyjmuje się konkretną liczbę otrzymaną za pomocą estymatora, na podstawie próby losowej.
Estymacja przedziałowa - polega na tym, że konstruuje się pewien przedział (zwany przedziałem ufności), o którym możemy powiedzieć, że z określonym prawdopodobieństwem 1-α będzie zawierał wartość szacowanego parametru. Prawdopodobieństwo 1-α określa się jako współczynnik ufności.
Współczynnik ufności (1-α) - jest to prawdopodobieństwo tego, że wyznaczając na podstawie n-elementowych prób dolną i górną granicę przedziału nieznana wartość parametru znajduje się w tym przedziale.
Wpływ wsp. ufności na precyzję: 1. Im większa liczba obserwacji, tym krótszy przedział ufności =>większa precyzja. 2. Im większa wartość współczynnika ufności, tym dłuższy przedział => mniejsza precyzja.
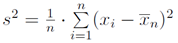
Wzór na estymację punktową dla wariancji: Wariancja z próby
jest estymatorem wariancji σ².
W3
Hipoteza statystyczna - jest to dowolne przypuszczenie dotyczące nieznanego rozkładu statystycznego jednej zmiennej lub łącznego rozkładu wielu zmiennych w populacji.
Hipotezy parametryczne - dotyczą nieznanych wartości parametrów rozkładu statystycznego, takich jak: wartość przeciętna, wariancja, czy wskaźnik struktury.
Hipotezy nieparametryczne - są to przypuszczenia na temat klasy rozkładów, do których należą: rozkład statystyczny w populacji, postaci rozkładu cechy statystycznej, współzależności cech lub losowości próby.
Hipoteza zerowa - H0; podstawowa hipoteza statystyczna sprawdzana danym testem. Nie zawsze musi być hipotezą prostą.
Hipoteza alternatywna - H1; hipoteza statystyczna konkurencyjna w stosunku do H0. Na ogół jest to hipoteza złożona.
Błąd I-ego rodzaju - jest to błąd polegający na odrzuceniu hipotezy zerowej, gdy jest ona prawdziwa.
Błąd II-ego rodzaju - jest to błąd polegający na przyjęciu hipotezy zerowej, gdy jest ona fałszywa.
Poziom istotności (α) - jest to prawdopodobieństwo błędu I-ego rodzaju.
Moc testu - jest to prawdopodobieństwo odrzucenia testowanej hipotezy, gdy jest ona fałszywa. Innymi słowy jest to prawdopodobieństwo NIE popełnienia błędu II-ego rodzaju. Oznaczenie: 1-β.
Położenie obszaru krytycznego zależy od konstrukcji hipotezy alternatywnej (H1).
W4
Nieparametryczne testy istotności: +testy losowości; +testy niezależności; +testy zgodności.
Testy losowości - weryfikują hipotezę, że próba ma charakter losowy.
Testy niezależności - sprawdzają hipotezę o niezależności dwóch zmiennych losowych.
Testy zgodności - 1. Służące do weryfikacji hipotez o postaci funkcyjnej rozkładu populacji generalnej. 2. Służące do weryfikacji hipotez, że dystrybuanty dwóch lub więcej zmiennych losowych są identyczne.
W5
Funkcja regresji - to analityczne przyporządkowanie średniej wartości zmiennej zależnej konkretnym wartościom zmiennej niezależnej.
Funkcja regresji I-go rodzaju - relacjom zmiennych zależnych przyporządkowuje średnie warunkowe zmiennej niezależnej.
Funkcja regresji II-go rodzaju - jest to przybliżenie funkcji regresji I-go rodzaju, opisujące zależność korelacyjną zmiennych losowych w próbie.
Wariancja resztowa - nie posiada interpretacji.
Błąd standardowy reszt (Su) - informuje jakie jest przecięte odchylenie wartości empirycznych zmiennej objaśnianej od wartości teoretycznych.
Wsp. zmienności losowej (Vu) - inf. jaki % śr. arytm. stanowi błąd stand. reszt.
Wsp. zbieżności losowej (φ²) - wyjaśnia jaka część zmian wartości zmiennej objaśnianej nie została wyjaśniona zmianami zmiennych objaśniających.
![]()
Wsp. determinacji (R²) - inf. jaka część zmian wartości zmiennej objaśnianej została wyjaśniona przez oszacowaną funkcję regresji.
Średnie błędy ocen parametrów (błędy szacunku): S(a0) i S(a1) - inf. o ile przeciętnie różniłyby się oszacowane parametry od ich prawdziwych wartości, gdyby szacunku dokonywać wielokrotnie na próbach o tej samej liczebności.
W1
Prawdopodobieństwo - jest to miara zdarzenia losowego.
Zmienna losowa - jest to taka zmienna, która przybiera różne wartości liczbowe z określonymi prawdopodobieństwami.
Zmienna losowa jest skokowa (dyskretna) - jeżeli zbiór wartości, które może przyjmować zmienna jest skończony lub przeliczalny.
Zmienna losowa jest ciągła - jeżeli zbiór wartości, które może przyjmować zmienna jest nieprzeliczalny.
Dystrybuanta zmiennej losowej - jest to funkcja: F(x) = P(X<x)
Rozkłady zmiennej losowej skokowej: +zero-jedynkowy; +dwumianowy; +Poissona.
W2
Estymator - jest to zmienna losowa o określonym rozkładzie. Jego podstawowe charakterystyki to wartość oczekiwana E(Tn) i odchylenie standardowe D(Tn).
Własności dobrego estymatora: +nieobciążoność; +zgodność; +wysoka efektywność.
Estymator jest asymptotycznie nieobciążony, gdy: lim b(Tn) = 0
Estymator jest zgodny, jeżeli: plim Tn = θ
Estymacja punktowa - polega na tym, że za ocenę parametru przyjmuje się konkretną liczbę otrzymaną za pomocą estymatora, na podstawie próby losowej.
Estymacja przedziałowa - polega na tym, że konstruuje się pewien przedział (zwany przedziałem ufności), o którym możemy powiedzieć, że z określonym prawdopodobieństwem 1-α będzie zawierał wartość szacowanego parametru. Prawdopodobieństwo 1-α określa się jako współczynnik ufności.
Współczynnik ufności (1-α) - jest to prawdopodobieństwo tego, że wyznaczając na podstawie n-elementowych prób dolną i górną granicę przedziału nieznana wartość parametru znajduje się w tym przedziale.
Wpływ wsp. ufności na precyzję: 1. Im większa liczba obserwacji, tym krótszy przedział ufności =>większa precyzja. 2. Im większa wartość współczynnika ufności, tym dłuższy przedział => mniejsza precyzja.
Wzór na estymację punktową dla wariancji: Wariancja z próby
jest estymatorem wariancji σ².
W3
Hipoteza statystyczna - jest to dowolne przypuszczenie dotyczące nieznanego rozkładu statystycznego jednej zmiennej lub łącznego rozkładu wielu zmiennych w populacji.
Hipotezy parametryczne - dotyczą nieznanych wartości parametrów rozkładu statystycznego, takich jak: wartość przeciętna, wariancja, czy wskaźnik struktury.
Hipotezy nieparametryczne - są to przypuszczenia na temat klasy rozkładów, do których należą: rozkład statystyczny w populacji, postaci rozkładu cechy statystycznej, współzależności cech lub losowości próby.
Hipoteza zerowa - H0; podstawowa hipoteza statystyczna sprawdzana danym testem. Nie zawsze musi być hipotezą prostą.
Hipoteza alternatywna - H1; hipoteza statystyczna konkurencyjna w stosunku do H0. Na ogół jest to hipoteza złożona.
Błąd I-ego rodzaju - jest to błąd polegający na odrzuceniu hipotezy zerowej, gdy jest ona prawdziwa.
Błąd II-ego rodzaju - jest to błąd polegający na przyjęciu hipotezy zerowej, gdy jest ona fałszywa.
Poziom istotności (α) - jest to prawdopodobieństwo błędu I-ego rodzaju.
Moc testu - jest to prawdopodobieństwo odrzucenia testowanej hipotezy, gdy jest ona fałszywa. Innymi słowy jest to prawdopodobieństwo NIE popełnienia błędu II-ego rodzaju. Oznaczenie: 1-β.
Położenie obszaru krytycznego zależy od konstrukcji hipotezy alternatywnej (H1).
W4
Nieparametryczne testy istotności: +testy losowości; +testy niezależności; +testy zgodności.
Testy losowości - weryfikują hipotezę, że próba ma charakter losowy.
Testy niezależności - sprawdzają hipotezę o niezależności dwóch zmiennych losowych.
Testy zgodności - 1. Służące do weryfikacji hipotez o postaci funkcyjnej rozkładu populacji generalnej. 2. Służące do weryfikacji hipotez, że dystrybuanty dwóch lub więcej zmiennych losowych są identyczne.
W5
Funkcja regresji - to analityczne przyporządkowanie średniej wartości zmiennej zależnej konkretnym wartościom zmiennej niezależnej.
Funkcja regresji I-go rodzaju - relacjom zmiennych zależnych przyporządkowuje średnie warunkowe zmiennej niezależnej.
Funkcja regresji II-go rodzaju - jest to przybliżenie funkcji regresji I-go rodzaju, opisujące zależność korelacyjną zmiennych losowych w próbie.
Wariancja resztowa - nie posiada interpretacji.
Błąd standardowy reszt (Su) - informuje jakie jest przecięte odchylenie wartości empirycznych zmiennej objaśnianej od wartości teoretycznych.
Wsp. zmienności losowej (Vu) - inf. jaki % śr. arytm. stanowi błąd stand. reszt.
Wsp. zbieżności losowej (φ²) - wyjaśnia jaka część zmian wartości zmiennej objaśnianej nie została wyjaśniona zmianami zmiennych objaśniających.
Wsp. determinacji (R²) - inf. jaka część zmian wartości zmiennej objaśnianej została wyjaśniona przez oszacowaną funkcję regresji.
Średnie błędy ocen parametrów (błędy szacunku): S(a0) i S(a1) - inf. o ile przeciętnie różniłyby się oszacowane parametry od ich prawdziwych wartości, gdyby szacunku dokonywać wielokrotnie na próbach o tej samej liczebności.
Wyszukiwarka
Podobne podstrony:
I i II tura - pyt + odp, Studia, Zastosowanie statystyki w zarzadzaniu
SOP-zagadnienia na exam, Dokumenty STUDIA SKANY TEXT TESTY, ADMINISTRACJA UNIWEREK WROCŁAW MAGISTER,
Zagadnienia na kolokwium OEBHP, (Sylwia) studia semestr 3, Analiza żywności, Bhp i ergonomia
Lasy miejskie – przegląd wybranych zagadnień na podstawie literatury
Wybrane zagadnienia z części ogólnej prawa cywilnego, studia, semestr V, zobowiazania
reszta zagadnień na egzamin, Notatki Europeistyka Studia dzienne, II semestr
Zagadnienia na ćwiczenia z Biologii molekularnejFarm2009, Studia i edukacja, farmacja
Zagadnienia na towaroznawstwo handlowo celne, Studia, I o, rok III, sem VI, Towaroznawstwo handlowo-
na egzamin sciaga testowa, Studia, III rok, Gospodarka Nieruchomosciami, testy GN
ZAGADNIENIA NA EXAM Z GENETYKI 10
więcej podobnych podstron