Konstrukcje stalowe
projekt 3
Marek Tabor
Rok 3B Gr 14B WIMiR
1. Wstępny dobór przekrojów
Dobór przekroju zaczynam od słupa nr 2 tj. belki ponieważ od jej
wymiarów geometrycznych będą zależały wymiary słupa. Słup
musi być szerszy od belki aby byla możliwość położenia spoiny
na całym obwodzie.
słup nr 2 (belka)
Materiał na słup przyjmuję 18G2A
siły przekrojowe działające na słup:
wytrzymałość:
wstepne pole przekroju
wstepny wskaźnik wytrzymałośći
dobieram z normy:
Dwuteownik IPE 330
Cechy przekroju:
Charakterystyka:
Wymiary:
Napreżenia zastepcze
warunek spełniony, przekrój dobrany prawidłowo
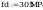
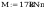
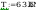
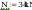
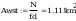
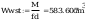
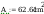
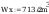
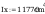
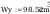
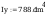
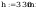
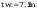
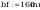
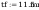
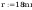
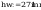
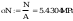
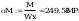
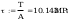
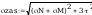
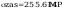
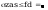
słup nr 1
Materiał na słupy przyjmuję 18G2A
siły przekrojowe działające na słup:
wytrzymałość:
wstępne pole przekroju
wstepny wskaźnik wytrzymałości
Ze względu na to że dla ceownika tak duży wskażnik wytrzymałości
jest tylko względem krótszego boku a wcześniej dobrany został
dwuteownik o szerokość 160mm muszę wybrać inny profil.
dobieram z normy:
Dwuteownik szerokostopowy HE 220 B
Cechy przekroju:
Wymiary:
Charakterystyka:
Napreżenia zastepcze
Warunek spełniony, przekrój dobrany prawidłowo
Słup nr3
Ponieważ siły działajace w słupie nr 3 są mniejsze od sił w
słupie nr 1 dobieram
przekrój słupa nr 3 taki sam jak słupa nr 1 tj. HE 220 B ze
względów konstrukcyjnych
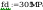
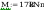
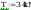
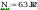
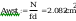
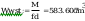
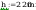
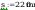
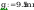
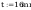
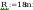
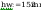
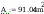
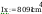
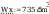
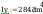
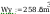
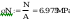
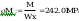
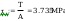
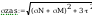
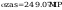
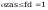
2. Sprawdzenie nośności
połączenia belki dwuteowej IPE 330 ze słupem HE 220B wykonanego
za pomocą spoin pachwinowych.
odczytuję z tablicy 18:
alfa prostopadłe
alfa równoległe
przyjęto spoine łącząca środnik ze słupem as:
spoina łącząca półke ze słupem:
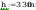
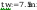
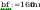
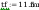
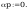
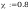
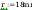
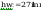
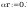
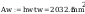
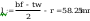
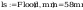
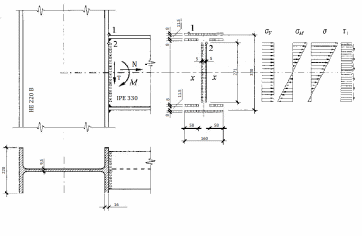
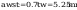
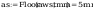
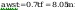
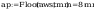
Pole powirzchni spoiny:
Pole powierzchni spoiny łączącej srodnik ze słupem
Moment bezwładności spoiny Ix:
Obliczanie naprężeń występujących w spoinie
Warunek dla punktu 1 ze wzoru (93)
przy czym
Warunek dla punktu 2 ze wzoru (93)
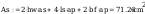
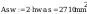
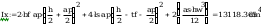
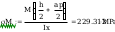
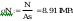
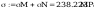
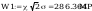
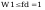
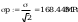
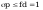
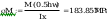
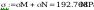
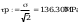
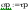
Wszystkie warunki spełnione, połaczenie zostało poprawnie
zaprojektowane
Węzeł B
W węzle B działają mniejsze siły przekrojowe niż w węzle A
więc nie ma potrzeby sprawdzania nośności spoiny
3. Sprawdzenie nośności
słupa nr 1
Ustalenie klasy przekroju HE 220 B
- dla środnik (tabl. 6, poz. a)
- półka (tabl. 6, poz. b)
przekrój zalicza sie do klasy 1
Dla klasy 1 ψ=1 a αp>1,0. Nośność obliczeniową przekroju
przy zginaniu określono wg wzoru (42), przy przyjęciu αp=1,07
Nośnmość obliczeniową przekroju przy osiowym ściskaniu wg wzoru
(33)
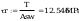
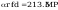
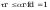
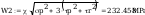
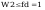
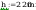
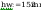
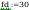
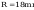
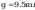
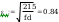
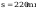
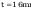

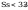
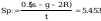
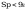
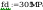
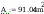
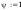
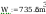
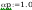
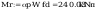
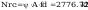
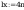
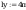
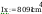
Smukłości słupa wynoszą
smukłość porownawcza wg wzoru(38)
smukłości względne wg wzoru (35) i współczynniki wyboczeniowe
współczynniki wyboczeniowe obliczam z zależności: λ=(1+λ2*n)-1/n
Moment krytyczny słupa określono jako dla pręta widełkowo
podpartego o węzłach poprzecznie nieprzesuwnych, obciążonego
liniowo zmiennymi momentami (wg tabl. 12 poz. a, β=0,55)
według tabl. Z1-2:
według wzorów (Z1-4) i (Z1-5)
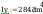
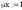
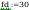
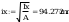
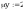
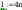
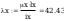
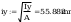
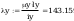
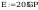
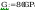
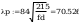
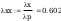
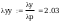
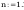
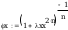
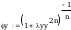
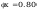
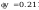
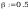
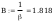
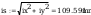
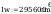
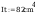
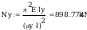
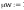
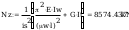
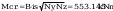
Według wzoru (50):
współczynnik wyboczeniowy dla krzywe a0, n=2,5:
Warunek nośności (stateczności) słupa ściskanego i zginanego wg
wzoru (58), w rozpatrywanym przypadku należy sprawdzić dwukrotnie.
dla ϕx=0,806 i βx=1
<1-Δx
składnik poprawkowy wg wzoru (57)
<0,1
dla ϕy=0,211 i β=0,55 oraz Δy=0
<1
Dodatkowo sprawdzono (β<1) warunek (54) w postaci:
<1
Wymagane warunki nośności są spełnione
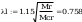
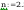
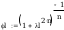
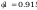
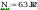
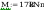
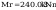
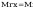
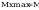
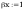
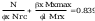
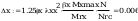
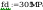
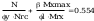
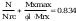
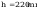
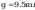
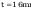
Sprawdzenie warunku smukłości przy ścinaniu wg tabl. 7
stąd nośność obliczeniową przekroju przy ścinaniu określono
wg wzoru (47)
przekrój powierzchni poddanej ścinaniu
Według punktu p. 4.5.2d spełniony jest warunek:
Vmax<Vo
nie jest więc wymagane sprawdzenie warunku (55)
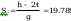
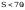
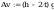
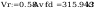
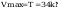
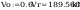
Wyszukiwarka
Podobne podstrony:
PhysHL P3 M01 MS
512 P3 N856
PhysHL P3 M05 TZ1 M
P3 PLAN KONSERWATORSKI (FORMAT 2000x2500)
P3
Banki2010 wykresy p3 [ www potrzebujegotowki pl ]
p3 2010 rus
ŁMgoss wod cw 1 p3
PhysHL P3 M06 TZ2
Mathcad p3
p3
Zestaw zadan I Kalamajska solns p3
arkusz p3 id 68810 Nieznany
11ak19 p3 circuit 1265id 13070 Nieznany
p3
PhyHL N07 P3 TZ0 MS
elektra p3
p3 sprawozdanie obliczone
IB math 2008 HL p3
protokol p3