Konstrukcje stalowe

projekt 3

Marek Tabor

Rok 3B Gr 14B WIMiR

1. Wstępny dobór przekrojów

Dobór przekroju zaczynam od słupa nr 2 tj. belki ponieważ od jej wymiarów geometrycznych
będą zależały wymiary słupa. Słup musi być szerszy od belki aby byla możliwość położenia
spoiny na całym obwodzie.

słup nr 2 (belka)

Materiał na słup przyjmuję
18G2A

siły przekrojowe działające na słup:

wytrzymałość: fd

305MPa

:=

M

178kN m

⋅

:=

T

63.5kN

:=

N

34kN

:=

Awst

N

fd

1.115 cm

2

⋅

=

:=

wstepne pole przekroju

Wwst

M

fd

583.607 cm

3

⋅

=

:=

wstepny wskaźnik wytrzymałośći

dobieram z normy:

Dwuteownik IPE 330

Cechy przekroju:

Charakterystyka:

A

62.61cm

2

:=

Wx

713.2cm

3

:=

Ix

11770cm

4

:=

Wy

98.52cm

3

:=

Iy

788.1cm

4

:=

Wymiary:

h

330mm

:=

tw

7.5mm

:=

bf

160mm

:=

tf

11.5mm

:=

r

18mm

:=

hw

271mm

:=

σN

N

A

5.4304 MPa

⋅

=

:=

σM

M

Wx

249.58 MPa

⋅

=

:=

τ

T

A

10.142 MPa

⋅

=

:=

σzas

σN

σM

+

(

)

2

3

τ

2

⋅

+

:=

Napreżenia zastepcze

σzas

255.614 MPa

⋅

=

σzas

fd

≤

1

=

warunek spełniony, przekrój dobrany prawidłowo

słup nr 1

Materiał na słupy przyjmuję
18G2A

siły przekrojowe działające na słup:

wytrzymałość:

fd

305MPa

:=

M

178kN m

⋅

:=

T

34kN

:=

N

63.5kN

:=

Awst

N

fd

2.082 cm

2

⋅

=

:=

wstępne pole przekroju

Wwst

M

fd

583.607 cm

3

⋅

=

:=

wstepny wskaźnik wytrzymałości

Ze względu na to że dla ceownika tak duży wskażnik wytrzymałości jest tylko względem
krótszego boku a wcześniej dobrany został dwuteownik o szerokość 160mm muszę wybrać
inny profil.

dobieram z normy:

Dwuteownik szerokostopowy HE 220 B

Cechy przekroju:

Wymiary:

h

220mm

:=

s

220mm

:=

g

9.5mm

:=

t

16mm

:=

R

18mm

:=

hw

152mm

:=

Charakterystyka:

A

91.04cm

2

:=

Ix

8091cm

4

:=

Wx

735.5cm

3

:=

Iy

2843cm

4

:=

Wy

258.5cm

3

:=

σN

N

A

6.975 MPa

⋅

=

:=

σM

M

Wx

242.01 MPa

⋅

=

:=

τ

T

A

3.735 MPa

⋅

=

:=

σzas

σN

σM

+

(

)

2

3

τ

2

⋅

+

:=

Napreżenia zastepcze

σzas

249.071 MPa

⋅

=

σzas

fd

≤

1

=

Warunek spełniony, przekrój dobrany prawidłowo

Słup nr3

Ponieważ siły działajace w słupie nr 3 są mniejsze od sił w słupie nr 1 dobieram
przekrój słupa nr 3 taki sam jak słupa nr 1 tj. HE 220 B ze względów konstrukcyjnych

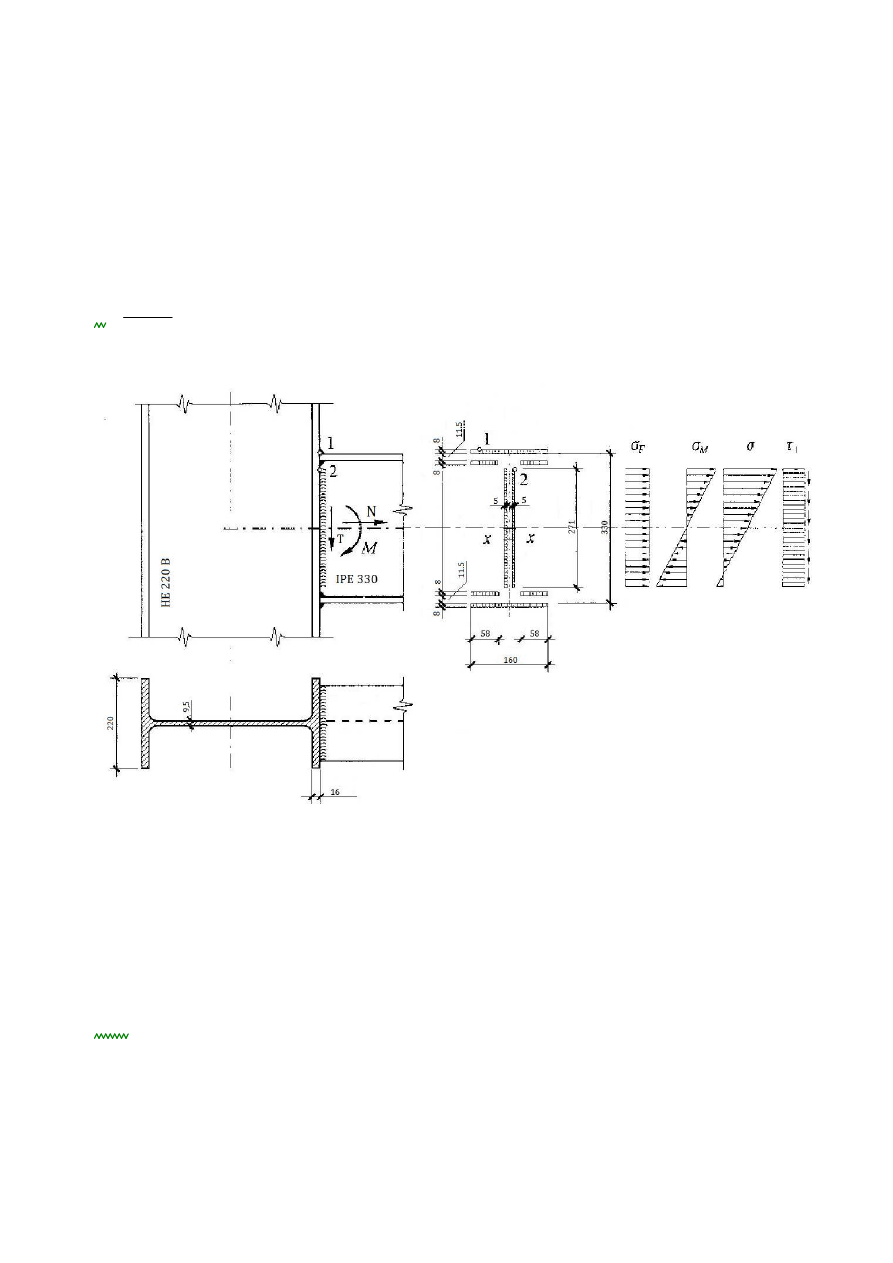
2. Sprawdzenie nośności połączenia belki dwuteowej IPE 330 ze słupem
HE 220B wykonanego za pomocą spoin pachwinowych.

odczytuję z tablicy 18:

αp

0.8

:=

alfa prostopadłe

χ

0.85

:=

αr

0.7

:=

alfa równoległe

Aw

hw tw

⋅

2032.5 mm

2

⋅

=

:=

l

bf

tw

−

2

r

−

58.25 mm

⋅

=

:=

ls

Floor l mm

,

(

)

58 mm

⋅

=

:=

przyjęto spoine łącząca środnik ze słupem as:

awst

0.7 tw

⋅

5.25 mm

⋅

=

:=

as

Floor awst mm

,

(

)

5 mm

⋅

=

:=

spoina łącząca półke ze słupem:

awst

0.7 tf

⋅

8.05 mm

⋅

=

:=

ap

Floor awst mm

,

(

)

8 mm

⋅

=

:=

Pole powirzchni spoiny:

As

2 hw

⋅

as

⋅

4 ls

⋅ ap

⋅

+

2 bf

⋅

ap

⋅

+

71.26 cm

2

⋅

=

:=

Pole powierzchni spoiny łączącej srodnik ze słupem

Asw

2 hw

⋅

as

⋅

2710 mm

2

⋅

=

:=

Moment bezwładności spoiny Ix:

Ix

2 bf

⋅

ap

⋅

h

2

ap

2

+









2

⋅

4 ls

⋅ ap

⋅

h

2

tf

−

ap

2

−









2

⋅

+

2

as hw

3

⋅

12













⋅

+

13118.365 cm

4

⋅

=

:=

Obliczanie naprężeń występujących w spoinie

σM

M

h

2

ap

2

+









⋅

Ix

229.312 MPa

⋅

=

:=

σN

N

As

8.911 MPa

⋅

=

:=

σ

σM

σN

+

238.223 MPa

⋅

=

:=

Warunek dla punktu 1 ze wzoru (93)

W1

χ

2

⋅

σ

⋅

286.364 MPa

⋅

=

:=

W1

fd

≤

1

=

przy czym

σp

σ

2

168.449 MPa

⋅

=

:=

σp

fd

≤

1

=

Warunek dla punktu 2 ze wzoru (93)

σM

M 0.5 hw

⋅

(

)

⋅

Ix

183.857 MPa

⋅

=

:=

σ

σM

σN

+

192.768 MPa

⋅

=

:=

τp

σ

2

136.307 MPa

⋅

=

:=

σp

τp

:=

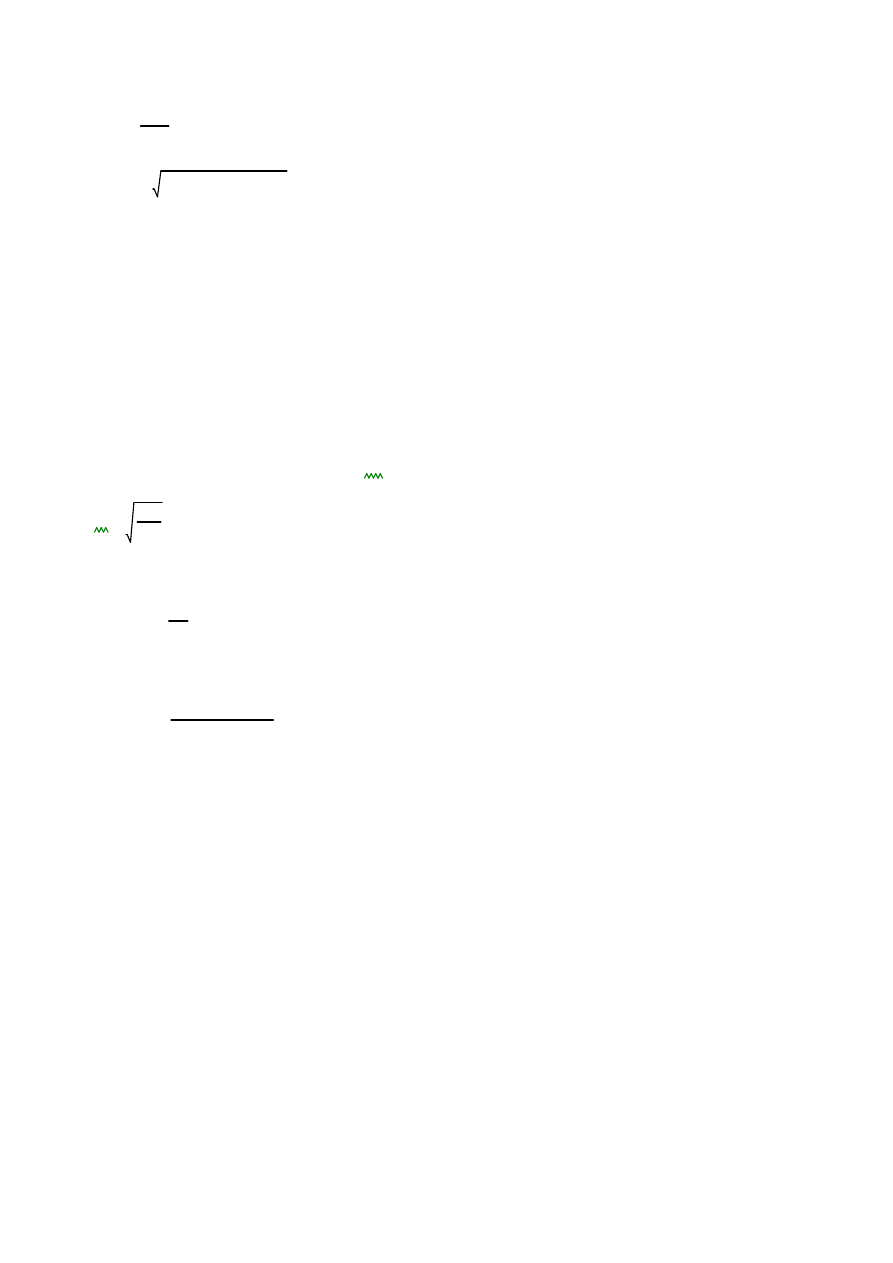
τr

T

Asw

12.546 MPa

⋅

=

:=

αr fd

⋅

213.5 MPa

⋅

=

τr

αr fd

⋅

≤

1

=

W2

χ

σp

2

3

τp

2

τr

2

+

(

)

⋅

+

⋅

232.458 MPa

⋅

=

:=

W2

fd

≤

1

=

Wszystkie warunki spełnione, połaczenie zostało poprawnie zaprojektowane

Węzeł B

W węzle B działają mniejsze siły przekrojowe niż w węzle A więc nie ma potrzeby
sprawdzania nośności spoiny

3. Sprawdzenie nośności słupa nr 1

Ustalenie klasy przekroju HE 220 B

fd

305

:=

ε

215

fd

0.84

=

:=

- dla środnik (tabl. 6, poz. a)

Ss

hw

g

16

=

:=

Ss

33

ε

<

- półka (tabl. 6, poz. b)

Sp

0.5 s

g

−

2 R

⋅

−

(

)

t

5.453

=

:=

Sp

9

ε

<

przekrój zalicza sie do klasy 1

Dla klasy 1 ψ=1 a αp>1,0. Nośność obliczeniową przekroju przy zginaniu określono wg
wzoru (42), przy przyjęciu αp=1,07

Mr

αp W

⋅

fd

⋅

240.03 kN m

⋅

⋅

=

:=

Nośnmość obliczeniową przekroju przy osiowym ściskaniu wg wzoru (33)

Nrc

ψ A

⋅ fd

⋅

2776.72 kN

⋅

=

:=

Smukłości słupa wynoszą

μx

1

:=

fd

305

:=

μy

2

:=

l

4m

:=

λx

μx lx

⋅

ix

42.43

=

:=

λy

μy ly

⋅

iy

143.159

=

:=

smukłość porownawcza wg wzoru(38)

λp

84

215

fd

⋅

70.526

=

:=

smukłości względne wg wzoru (35) i współczynniki wyboczeniowe

λxx

λx

λp

0.602

=

:=

λyy

λy

λp

2.03

=

:=

n

1.2

:=

współczynniki wyboczeniowe obliczam z zależności: λ=(1+λ

2*n

)

-1/n

ϕx

1

λxx

2 n

⋅

+

(

)

1

−

n

:=

ϕy

1

λyy

2 n

⋅

+

(

)

1

−

n

:=

ϕx

0.806

=

ϕy

0.211

=

Moment krytyczny słupa określono jako dla pręta widełkowo podpartego o węzłach poprzecznie
nieprzesuwnych, obciążonego liniowo zmiennymi momentami (wg tabl. 12 poz. a, β=0,55)

β

0.55

:=

według tabl. Z1-2:

B

1

β

1.818

=

:=

is

ix

2

iy

2

+

109.591 mm

⋅

=

:=

według wzorów (Z1-4) i (Z1-5)

Iw

295600cm

6

:=

It

82cm

4

:=

Ny

π

2

E Iy

⋅

μy l

⋅

(

)

2

898.774 kN

⋅

=

:=

μw

1

:=

Nz

1

is

2

π

2

E

⋅ Iw

⋅

μw l

⋅

(

)

2

G It

⋅

+













8574.437 kN

⋅

=

:=

Mcr

B is

⋅

Ny Nz

⋅

⋅

553.145 kN m

⋅

⋅

=

:=

Według wzoru (50):

λl

1.15

Mr

Mcr

⋅

0.758

=

:=

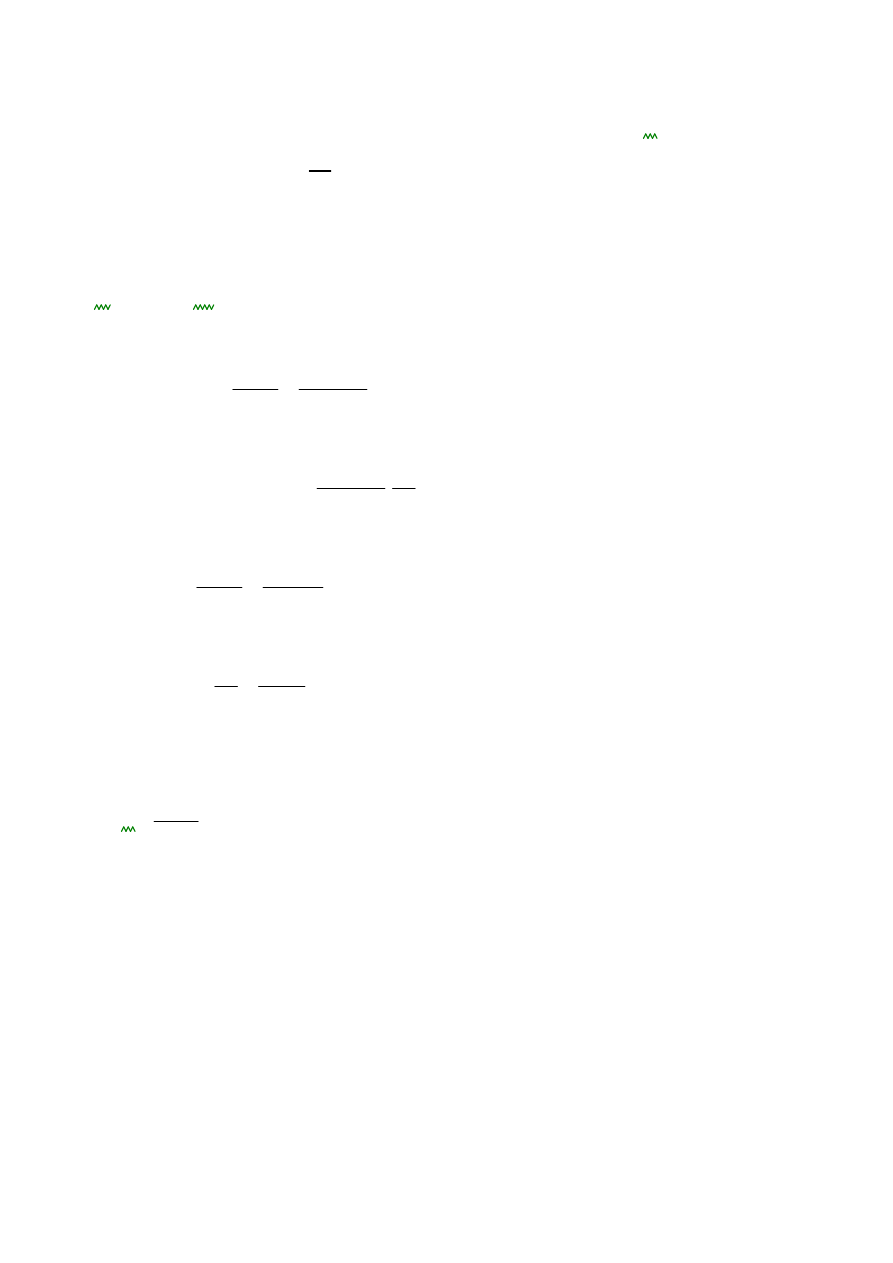
współczynnik wyboczeniowy dla krzywe a0, n=2,5:

n

2.5

:=

ϕl

1

λl

2 n

⋅

+

(

)

1

−

n

:=

ϕl

0.915

=

Warunek nośności (stateczności) słupa ściskanego i zginanego wg wzoru (58), w rozpatrywanym przypadku
należy sprawdzić dwukrotnie.

N

63.5kN

:=

M

178kN m

⋅

:=

Mr

240.03 kN m

⋅

⋅

=

Mrx

Mr

:=

Mxmax

M

:=

βx

1

:=

dla ϕx=0,806 i βx=1

N

ϕx Nrc

⋅

βx Mxmax

⋅

ϕl Mrx

⋅

+

0.839

=

<1-∆x

składnik poprawkowy wg wzoru (57)

∆x

1.25

ϕx

⋅

λxx

2

⋅

βx Mxmax

⋅

Mrx

⋅

N

Nrc

⋅

0.006

=

:=

<0,1

dla ϕy=0,211 i β=0,55 oraz ∆y=0

N

ϕy Nrc

⋅

β Mxmax

⋅

ϕl Mrx

⋅

+

0.554

=

<1

Dodatkowo sprawdzono (β<1) warunek (54) w postaci:

N

Nrc

Mxmax

ϕl Mrx

⋅

+

0.834

=

<1

Wymagane warunki nośności są spełnione

Sprawdzenie warunku smukłości przy ścinaniu wg tabl. 7

S

h

2 t

⋅

−

g

19.789

=

:=

S

70

ε

<

stąd nośność obliczeniową przekroju przy ścinaniu określono wg wzoru (47)

Av

h

2 t

⋅

−

(

) g

⋅

:=

przekrój powierzchni poddanej ścinaniu

Vr

0.58 Av

⋅

fd

⋅

315.943 kN

⋅

=

:=

Według punktu p. 4.5.2d spełniony jest warunek:

Vmax

T

34 kN

⋅

=

:=

Vo

0.6 Vr

⋅

189.566 kN

⋅

=

:=

Vmax<Vo

nie jest więc wymagane sprawdzenie warunku (55)

h

330mm

:=

tw

7.5mm

:=

bf

160mm

:=

tf

11.5mm

:=

r

18mm

:=

hw

271mm

:=

h

220mm

:=

hw

152mm

:=

R

18 mm

⋅

=

g

9.5 mm

⋅

=

s

220 mm

⋅

=

t

16 mm

⋅

=

fd

305MPa

:=

A

91.04cm

2

:=

ψ

1

:=

W

735.5cm

3

:=

αp

1.07

:=

lx

4m

:=

ly

4m

:=

Ix

8091cm

4

:=

Iy

2843cm

4

:=

ix

Ix

A

94.272 mm

⋅

=

:=

iy

Iy

A

55.882 mm

⋅

=

:=

E

205GPa

:=

G

80GPa

:=

fd

305MPa

:=

h

220 mm

⋅

=

g

9.5 mm

⋅

=

t

16 mm

⋅

=