Mathcad – opis do ćwiczenia

ZADANIE:

DLA JAKICH

D

,

h

OBJĘTOŚĆ WALCA

V

BĘDZIE NAJWIĘKSZA, PRZY

ZAŁOŻENIU, ŻE OBWÓD

GŁÓWNEGO PRZEKROJU

WALCA JEST STAŁY?

1. Rysunek walca

należy wczytać z pliku walec.bmp wydając polecenie Insert Picture

Po wydaniu tego polecenia pojawi się ramka z polem, w które należy wpisać

nazwę pliku lub wpisać ścieżkę prowadzącą do pliku graficznego (Mathcad

2000 pozwala importować grafikę zapisaną wyłącznie w plikach BMP). Nazwa

pliku musi być podana jako ciąg znaków, dlatego jej wpisywanie musi zaczynać

się od wprowadzenia znaku ”.

2. Rozwiązanie

Należy zdefiniować dwie funkcje O i V, według których liczone będą

odpowiednio obwód i objętość walca.

Obwód przekroju walca wyraża się wzorem: O=2D+2h, a objętość walca:

V=

π

D

2

/4h.

Obie funkcje muszą być uzależnione od zmiennych argumentów D i h.

PRz, KMK, 11’2004

Mathcad – opis do ćwiczenia

Zastosowana funkcja Maximize wymaga zbudowania bloku rozwiązania

(ang. Solve block), podobnie jak to było przy funkcji Find służącej do

rozwiązywania układów równań. Blok rozwiązania musi zawierać:

a.

Wartości startowych poszukiwanych parametrów D i h

b.

Słowo Given

c.

Zestaw warunków ograniczających, które podane muszą być z

wykorzystaniem operatorów logicznych dostępnych z paska

narzędziowego Boolean

W naszym przykładzie warunki będą trzy: dwa zapewniające fizyczny sens

zadania (wymiary walca większe od zera) oraz trzeci nakładający ograniczenia

na obwód walca. Proszę przyjąć konkretną liczbę np. O=100m.

d.

Użycia funkcji rozwiązującej:

Maximize(

funkcja_maksymalizowana, parametr1, parametr2

)

3. Obliczenie maksymalnej objętości walca

Uzyskane z funkcji Maximize rozwiązanie zawarte jest w

dwuelementowym wektorze (bo szukane były dwa parametry) pod przykładową

nazwą MAX.

MAX

33.333
16.667













m

=

W celu wykorzystania elementów tego wektora do obliczenia objętości V

musimy posłużyć się indeksowaniem macierzowym. Dlatego też indeksy użyte

w wywołaniu funkcji V muszą być wpisane w pola uzyskane poprzez

naciśnięciu klawisza [.

V MAX

1

MAX

2

,

(

)

14544.453m

3

=

PRz, KMK, 11’2004

Mathcad – opis do ćwiczenia

4. Graficzna ilustracja rozwiązania

Podstawowym założeniem jest przeprowadzanie obliczeń dla zbioru

wartości wzajemnie od siebie zależnych parametrów O, D i V.

Po podaniu wartości stałego parametru O następuje zdefiniowanie

arbitralnie przyjętego zakresu zmiennej i, która będzie używana jako zmienna

pomocnicza indeksująca pozostałe obliczenia. Przykładowo, proszę

przeprowadzić obliczenia dla kolejnych pięćdziesięciu kombinacji wymiarów

walca.

Po zdefiniowaniu odpowiedniego zakresu zmiennej i przystępujemy do

obliczeń poszczególnych wymiarów walca, które jednak są ze sobą wzajemnie

powiązane (wszystkie indeksy użyte w obliczeniach muszą być typu

macierzowego, zatem należy je wprowadzać po naciśnięciu klawisza [):

h

i

i 1 m

⋅

(

)

⋅

:=

Taki sposób zdefiniowania parametru h prowadzi do wygenerowania

tablicy wartości, które h może przyjąć. Pierwszym elementem tej tablicy jest

h

1

=1m, co jest zgodne z wcześniej przyjętym oczywistym założeniem, że h>0.

Na podstawie tak zdefiniowanego parametru h oblicza się następnie

parametr D. Wzór na D uzyskamy oczywiście z przekształcenia wcześniej

wykorzystywanego wzoru O=2D+2h czyli D=(O-2h)/2.

Zastosowanie indeksów macierzowych wyrażonych za pomocą zmiennej i

prowadzi do uzyskania tablicy z wartościami D odpowiadającymi

poszczególnym elementom z tablicy wartości zmiennej h – oznacza to, że

otrzymaliśmy pary parametrów D i h, przykładowo:

h

10

10 m

=

D

10

40 m

=

PRz, KMK, 11’2004

Mathcad – opis do ćwiczenia

Pozostaje, zatem obliczyć objętość walca dla takich par. Zapisując

definicję zmiennej V

i

otrzymujemy kolejną tablicę wartości, tym razem

parametru V.

V

i

π

D

i

( )

2

4

⋅

h

i

⋅

:=

Wracając do poprzedniego przykładu dla dziesiątej spośród rozważanych

par mamy:

V

10

12566.371m

3

=

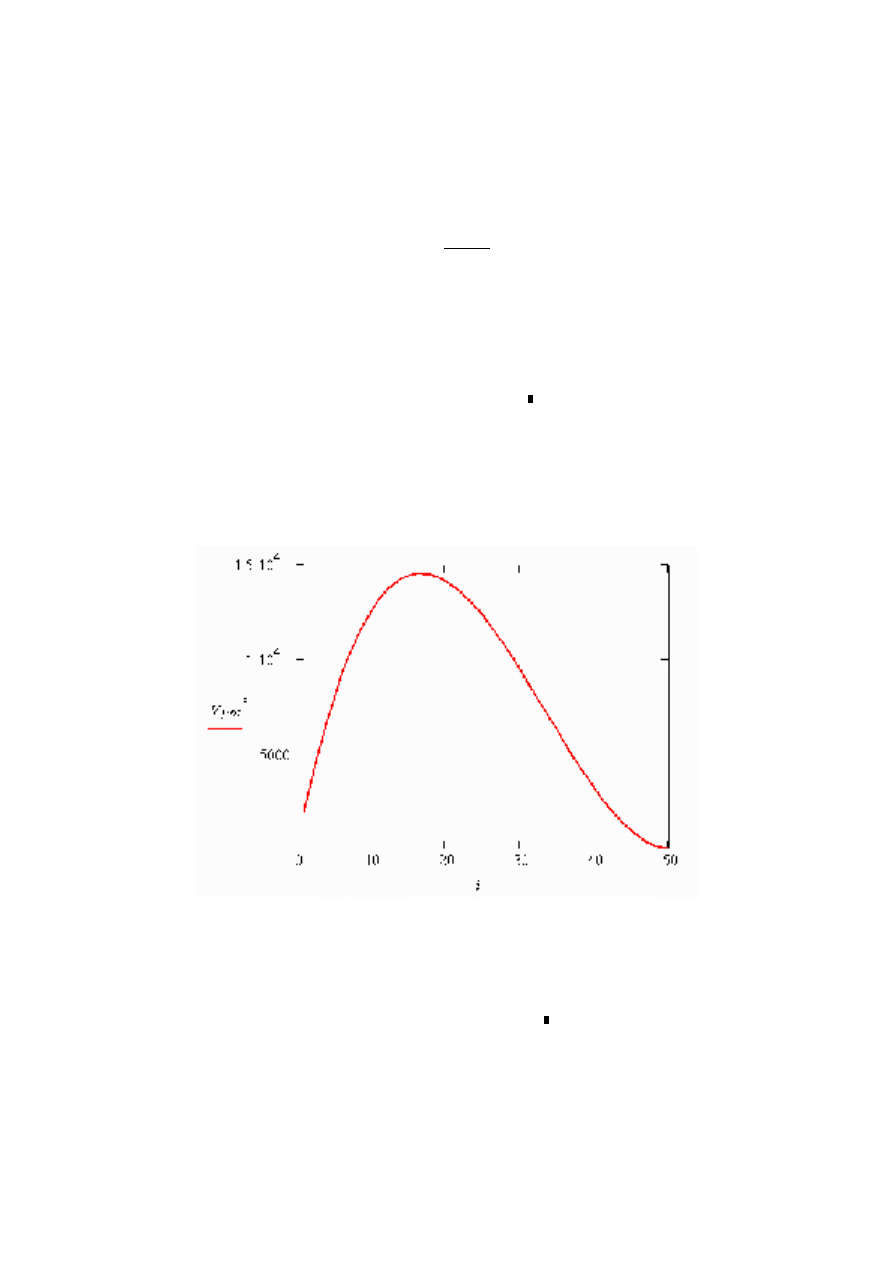
Pozostaje narysowanie wykresu ilustrującego zbiór wartości

przechowywany w tablicy V

i

. Jako odciętą należy podać na wykresie zmienną

indeksującą i.

Możliwe jest znalezienie największej spośród obliczonych objętości

znajdujących się w tablicy V. W tym celu wykorzystamy funkcję max().

max V

( )

14540.076 m

3

=

Uzyskane w ten sposób rozwiązanie różni się od obliczonego na podstawie

pary zmiennych (MAX

1

,MAX

2

), gdyż tym razem poszukiwanie parametrów

D i h zostało ograniczone do zbioru liczb całkowitych.

PRz, KMK, 11’2004