1. Pochodne

PRZYKŁAD
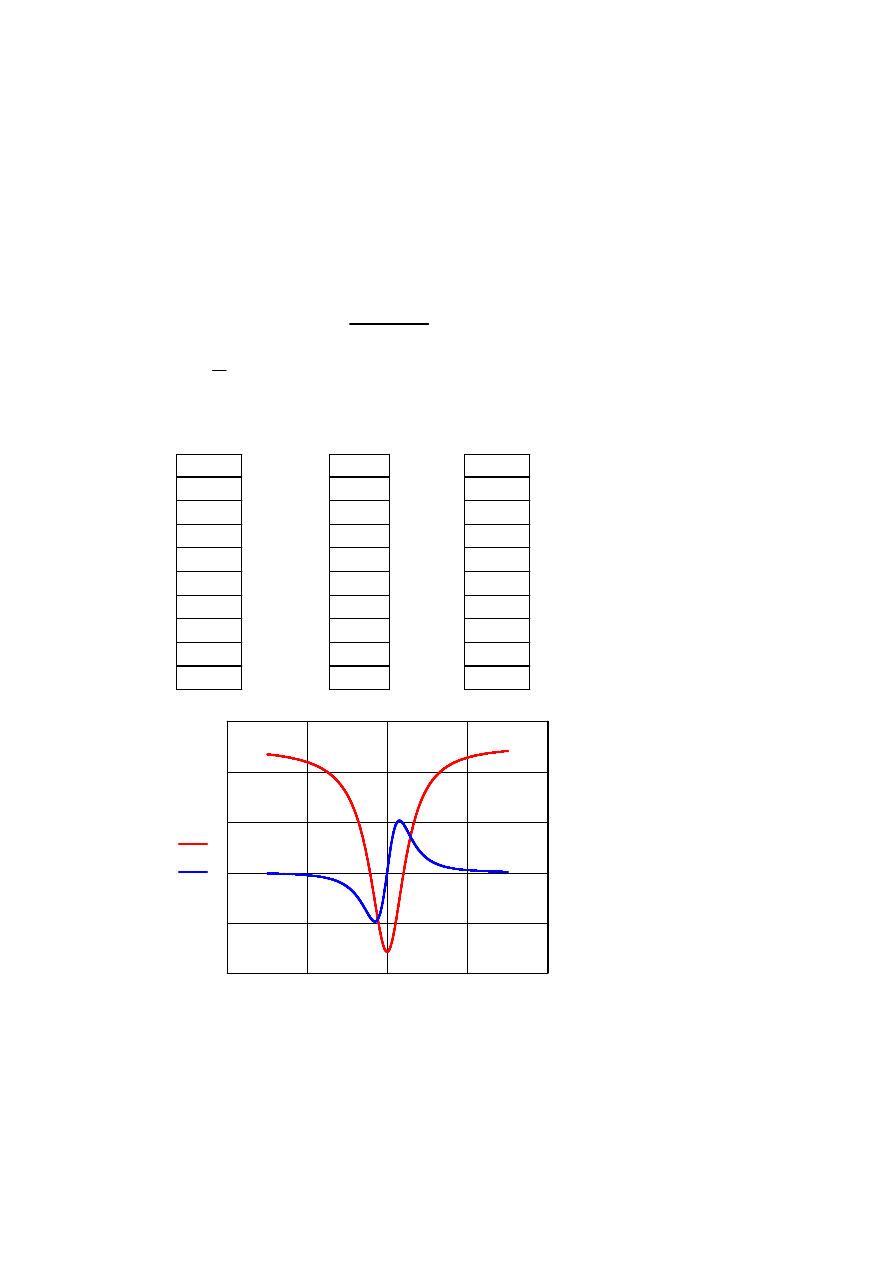
Dana jest funkcja f(x) w przedziale -15<x<15:
1. Wyznaczy

ć

pochodn

ą

funkcji df(x)

2. Sporz

ą

dzi

ć

tabelki, wspólne wykresy dla x, f(x), df(x)

3. Wykona

ć

przekształcenia symboliczne wykonaj ponownie wykresy

x

15

−

14.99

−

,

15

..

:=

f x

( )

5x

2

x

22

−

+

x

2

7

+

:=

df x

( )

x

f x

( )

d

d

:=

x

-15

-14.99

-14.98

-14.97

-14.96

-14.95

-14.94

-14.93

-14.92

...

=

f x

( )

4.69

4.689

4.689

4.689

4.688

4.688

4.687

4.687

4.687

...

=

df x

( )

-0.036

-0.036

-0.036

-0.036

-0.036

-0.036

-0.036

-0.036

-0.036

...

=

20

−

10

−

0

10

20

4

−

2

−

0

2

4

6

f x

( )

df x

( )

x

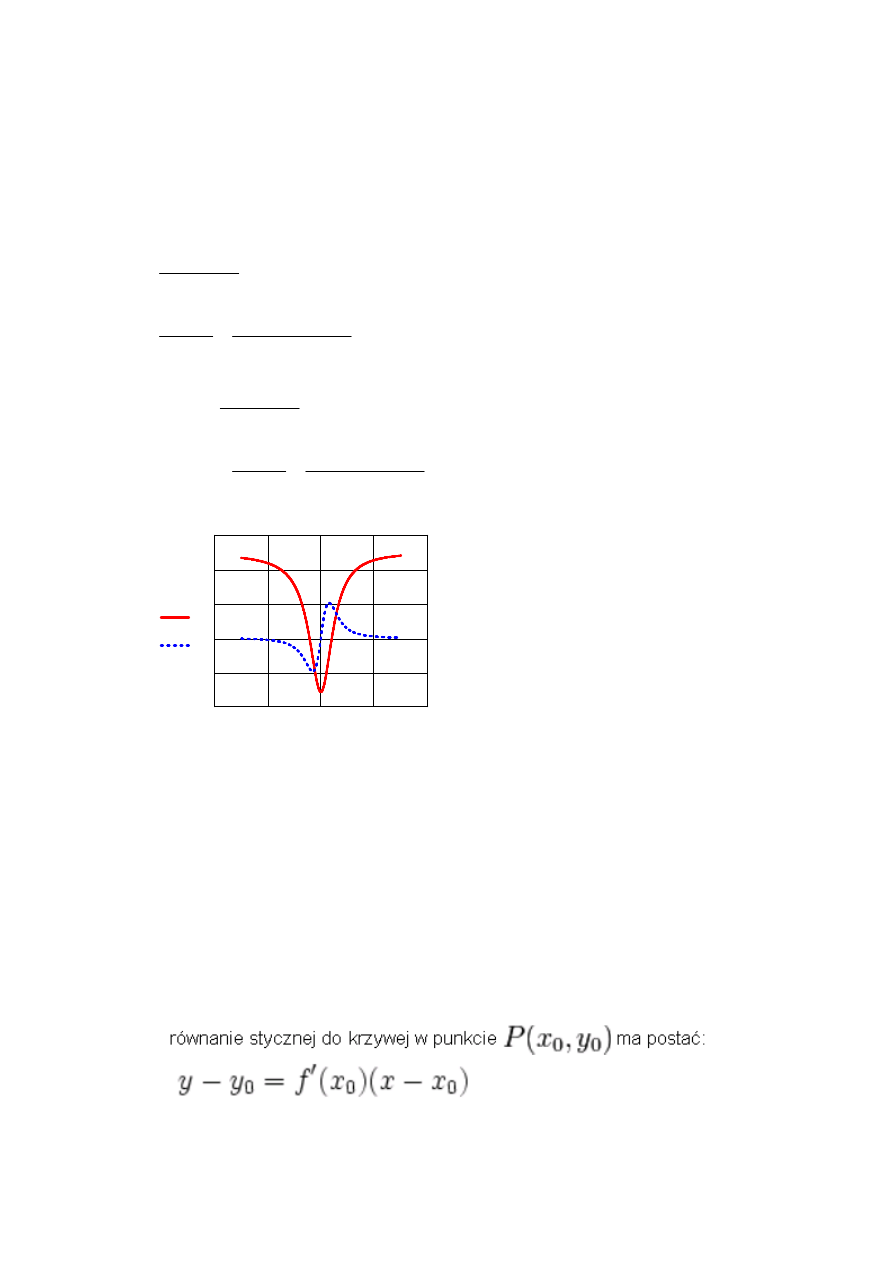
Przekształcenia symboliczne

Aby wyznaczy

ć

wzór pochodnej skopiuj poni

ż

ej wyra

ż

enie okre

ś

laj

ą

ce funkcj

ę

f(x) - to znaczy tylko praw

ą

stron

ę

definicji funkcji. Nast

ę

pnie umie

ść

kursor przy

zmiennej x i z menu Symbolics/Variable wybierz Differentiate.

5x

2

x

22

−

+

x

2

7

+

x

15

−

14.99

−

,

15

..

:=

10 x

⋅

1

+

x

2

7

+

2 x

⋅

5 x

2

⋅

x

+

22

−

(

)

⋅

x

2

7

+

(

)

2

−

f2 x

( )

5x

2

x

22

−

+

x

2

7

+

:=

df2 x

( )

10 x

⋅

1

+

x

2

7

+

2 x

⋅

5 x

2

⋅

x

+

22

−

(

)

⋅

x

2

7

+

(

)

2

−

















:=

20

−

10

−

0

10

20

4

−

2

−

0

2

4

6

f2 x

( )

df2 x

( )

x

Zadanie 1

Dana jest funkcja f(x) w przedziale 0<x<20:
1. Wyznaczy

ć

pochodn

ą

funkcji df(x)

2. Sporz

ą

dzi

ć

tabelki, wspólny wykres dla x, f(x), df(x)

3. Wykona

ć

przekształcenia symboliczne wykonaj ponownie wykresy

4. Oblicz współczynnik kierunkowy "KIER" (warto

ść

pochodnej) dla stycznej w

wybranym przez siebie punkcie "XA" oraz napisz równanie linii stycznej w tym
punkcie - jako funkcj

ę

LIN(x) - wstaw na wykres razem z x, f(x), df(x)

Funkcja: f(x)=2x +2 +9(cos(x/2))^2

Wskazówka:

2. Całki

PRZYKŁAD
Dana jest funkcja df3(x) w przedziale -4<x<4:
1. Wyznaczy

ć

całk

ę

funkcji df3(x)

2. Sporz

ą

dzi

ć

tabelki, wspólne wykresy dla x, f3(x), df3(x)

3. Wyznacz warto

ść

całki oznaczonej dla wybranego podprzedziału

4. Wykona

ć

przekształcenia symboliczne

x

4

−

3.99

−

,

4

..

:=

df3 x

( )

sin

x

2

























2

:=

f3 x

( )

x

df3 x

( )

⌠



⌡

d













x

2

sin x

( )

2

−

→

:=

x

-4

-3.99

-3.98

-3.97

-3.96

-3.95

-3.94

...

=

df3 x

( )

0.827

0.831

0.834

0.838

0.842

0.845

0.849

...

=

f3 x

( )

-2.378

-2.37

-2.362

-2.353

-2.345

-2.337

-2.328

...

=

4

−

2

−

0

2

4

3

−

2

−

1

−

0

1

2

3

df3 x

( )

f3 x

( )

x

4

−

4

x

df3 x

( )

⌠



⌡

d

4

sin 4

( )

−

→

4.757

=

PRZEKSZTAŁCENIA SYMBOLICZNE: Aby wyznaczy

ć

wzór całki skopiuj poni

ż

ej wyra

ż

enie

okre

ś

laj

ą

ce funkcj

ę

df3(x) - to znaczy tylko praw

ą

stron

ę

definicji funkcji. Nast

ę

pnie umie

ść

kursor przy zmiennej x i z menu Symbolics/Variable wybierz Integrate.

sin

x

2

























2

x

2

sin x

( )

2

−

Zadanie 2

Dana jest funkcja df2(x) w przedziale -1<x<1:
1. Wyznaczy

ć

całk

ę

funkcji df2(x)

2. Sporz

ą

dzi

ć

tabelki, wspólne wykresy dla x, f2(x), df2(x)

3. Wyznacz warto

ść

całki oznaczonej dla wybranego przez siebie

podprzedziału
4. Wykona

ć

przekształcenia symboliczne

Funkcja: df2(x)=-x^2 + (sinx)^2

3. Równania ró

ż

niczkowe w Mathcadzie

Funkcja Odesolve([vector], x, b, [npoints]) Wyznacza rozwi

ą

zanie zwykłego

równania ró

ż

niczkowego (ordinary differential equation - ODE), z warunkami

pocz

ą

tkowymi lub brzegowymi. Równanie musi by

ć

liniowe wzgl

ę

dem najwy

ż

szej

pochodnej, a liczba warunków pocz

ą

tkowych lub brzegowych musi by

ć

równa

rz

ę

dowi równania.

Argumenty:

vector - (opcjonalne) wektor nazw funkcji (tylko dla układu równa

ń

)

x - nazwa zmiennej wzgl

ę

dem której całkujemy

b - koniec przedziału całkowania

npoints - (opcjonalne) liczba punktów aproksymacji (domyslnie 1000)

Dla otrzymania rozwi

ą

zania z u

ż

yciem Odesolve nale

ż

y napisa

ć

Solve block,

Który rozpoczyna si

ę

słowem Given, nast

ę

pnie wpisujemy równanie i warunki

pocz

ą

tkowe, u

ż

ywaj

ą

c wytłuszczonego znaku równo

ś

ci (Boolean equal

uzyskiwanego przez Ctrl=). Pochodne mo

ż

na wstawia

ć

jako symbole z palety

Calculus lub wpisywa

ć

z kreskami "prim" uzyskiwanymi przez Ctrl[F7]

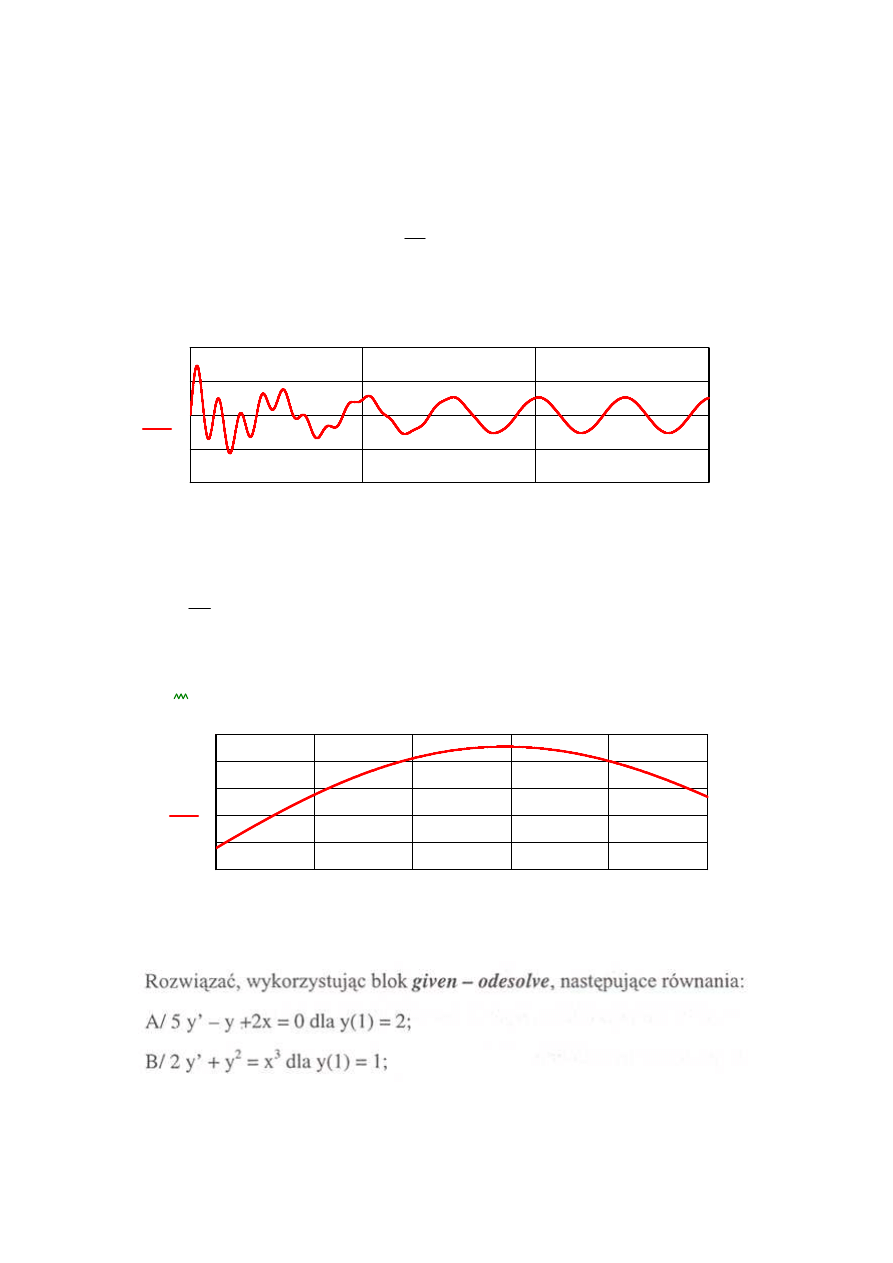
I Sposób

Given

x

0 0.01

,

150

..

:=

100 y'' x

( )

⋅

10 y' x

( )

⋅

+

101 y x

( )

⋅

+

50 cos

x 1

⋅

4













⋅

=

y 0

( )

0

=

y' 0

( )

1

=

y

Odesolve x 150

,

(

)

:=

0

50

100

150

2

−

1

−

0

1

2

y x

( )

x

II Sposób

Given

4

2

t

f t

( )

d

d

2

⋅

f t

( )

+

t

=

f 0

( )

4

=

f 5

( )

13.5

=

f

Odesolve t 5

,

(

)

:=

0

1

2

3

4

5

0

5

10

15

20

25

f t

( )

t

Zadanie 3

4. Upraszczanie i przekształcanie wyra

ż

e

ń

algebraicznych

Simplify (paleta SYMBOLIC)- upraszczenie skomplikowanych wyra

ż

e

ń

c

2

c

+

2

−

c

2

+

(

) c

⋅

simplify

1

1

c

−

→

Expand (paleta SYMBOLIC)- wymna

ż

a wyra

ż

enia

c

2

c

+

2

−

c

2

+

(

) c

⋅

expand

c

2

c

+

2

−

c

2

2 c

⋅

+

→

Collect (paleta SYMBOLIC)- grupowanie wyrazów i wyci

ą

ganie wspólnego

czynnika przed nawias

3s

2

d

5s

2

d

2

+

7s d

2

⋅

+

collect s

,

5 d

2

⋅

3 d

⋅

+

(

)

s

2

⋅

7 d

2

⋅

s

⋅

+

→

Substitute (paleta SYMBOLIC)- podstawianie

3c

3

2c

2

+

c

+

4

+

substitute c

z

4

+

=

,

3 z

3

⋅

38 z

2

⋅

+

161 z

⋅

+

232

+

→

Convert to Partial Fraction (paleta SYMBOLIC)- przedstawienie wyra

ż

enia jako

sume ułamków prostych

c

3

−

(

) c

6

+

(

)

⋅

c

2

−

(

) c

5

+

(

)

⋅

parfrac

8

7 c

5

+

(

)

⋅

8

7 c

2

−

(

)

⋅

−

1

+

→

Obliczanie granic funkcji (paleta CALCULUS)

∞

x

1

x

lim

→

0

→

Zadanie 4

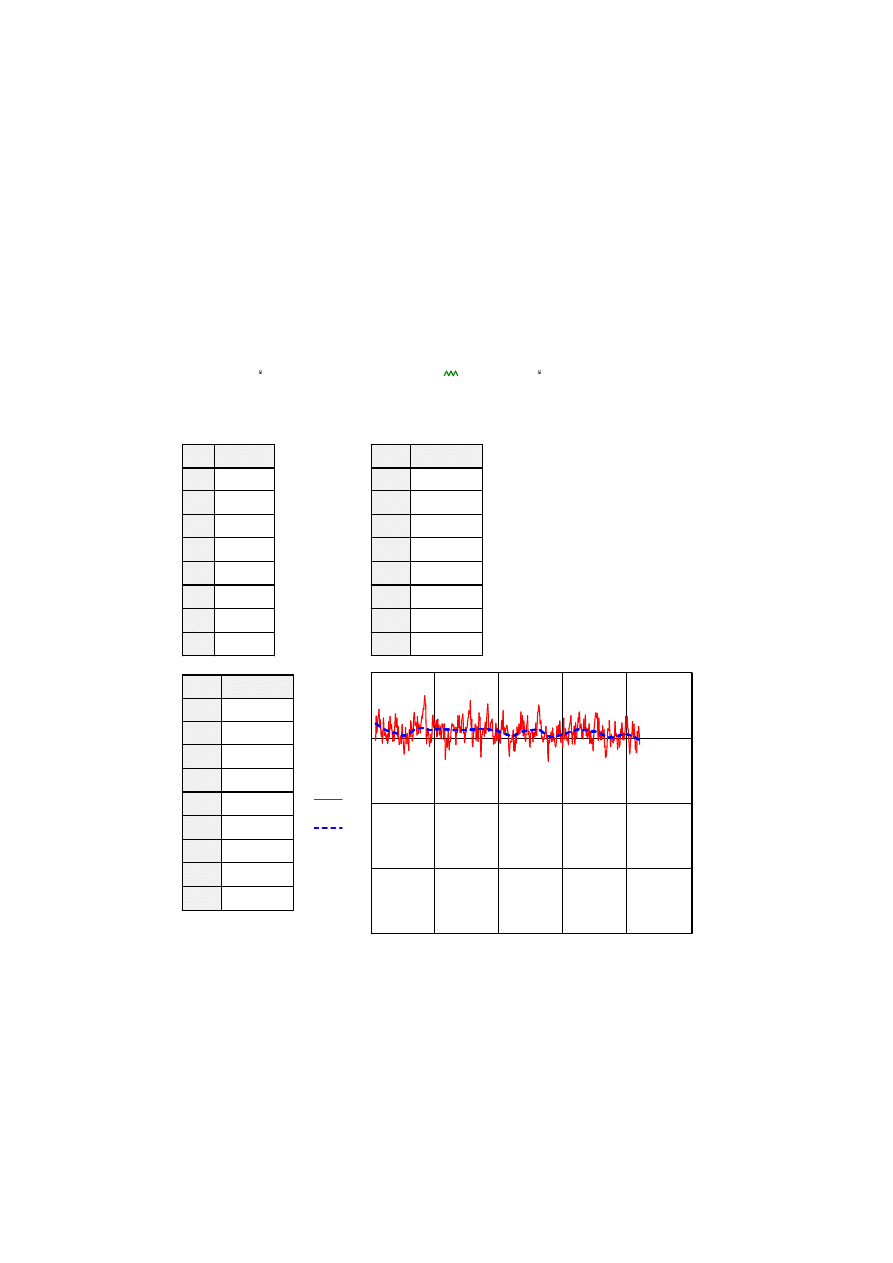
5. Wygładzanie funkcji

Wygładzanie danych to specyficzny rodzaj dopasowania krzywych. Zagadnienie
wygładzania ma cz

ę

sto miejsce, gdy dane wej

ś

ciowe zawieraj

ą

składniki

szumowe, które wymagaj

ą

eleminacji.

Jedn

ą

z funkcji słu

żą

c

ą

wygładzaniu danych jest supsmooth. Funkcja ta dopasowuje

odcinki linii na zasadzie liniowego dopasowania dla k s

ą

siednich punktów metod

ą

majmniejszych kwadratów.

Importujemy dane wybieracj

ą

c Insert/Data/File Input

Improtujemy kolejno Wspolrz

ę

dne x i y

x

x.txt

:=

y

y.txt

:=

x

1

1

2

3

4

5

6

7

8

13.5

15

16.5

18

19.5

21

22.5

...

=

y

1

1

2

3

4

5

6

7

8

0.059

0.067

0.061

0.062

0.065

0.066

0.067

...

=

z

supsmooth x y

,

(

)

:=

0

200

400

600

800

1 10

3

×

0

0.02

0.04

0.06

y

z

x

z

1

1

2

3

4

5

6

7

8

9

0.064

0.064

0.064

0.064

0.064

0.064

0.064

0.064

...

=

Zadanie 5

Przeprowad

ź

operacj

ę

wygładzania danych wykresu momentu, maj

ą

c dane

czas i moment w postaci plików *.txt, wykorzystuj

ą

c do tego funkcj

ę

supsmooth

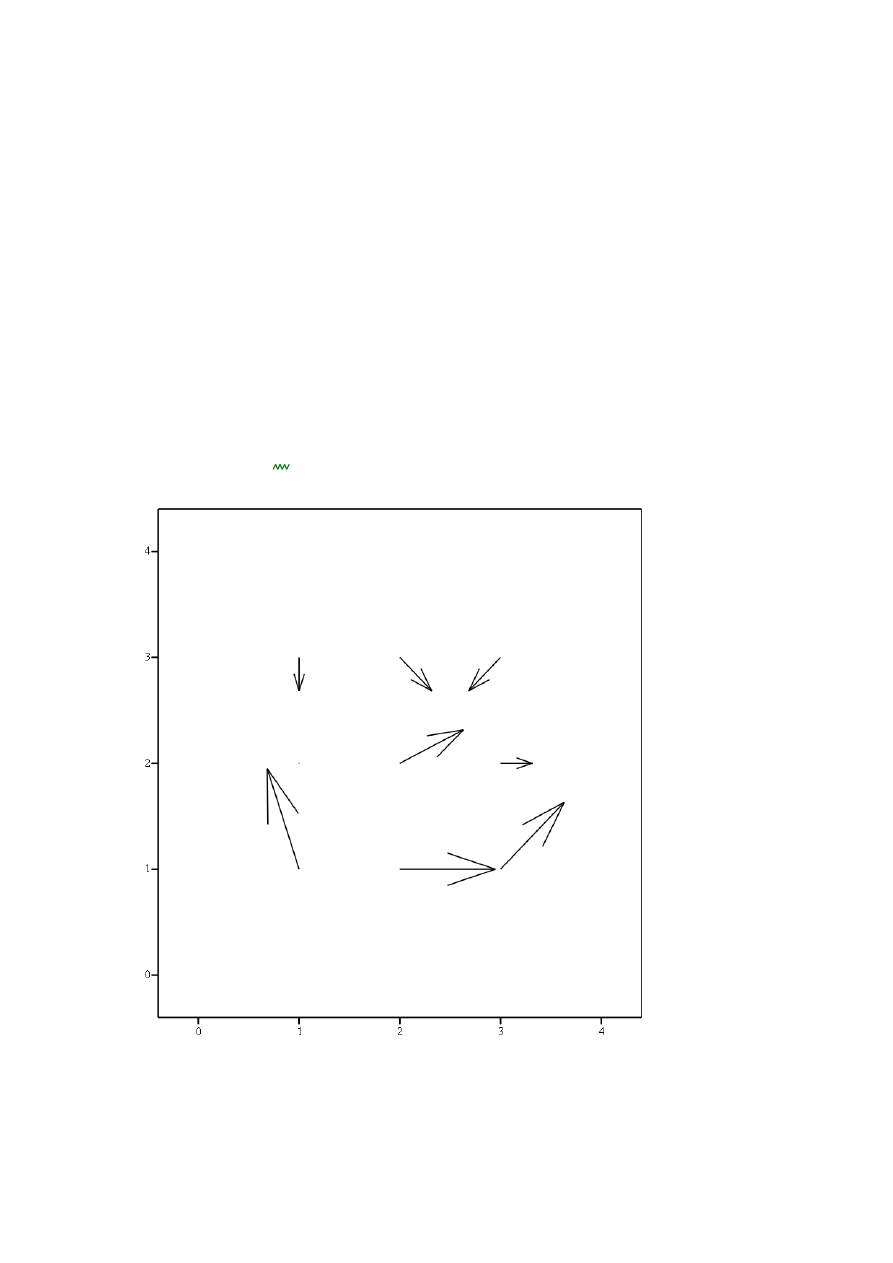
6. Wykresy wektorowe- Przepisz przykład

Wykres wektorowy (Vector Field Plot) słu

ż

y do graficznego przedstawiania wektorów.

Nie mo

ż

na na nim pokazywa

ć

funkcji. Poło

ż

enie liczby w macierzy okre

ś

la poło

ż

enie

wektora na wykresie.

W macierzy element z pierwszego wiersza i pierwszej kolumny to wektor zaczepiony w
punkcie (1,1), element tablicy z wiersza drugiego i kolumny pierwszej to wektor
zaczepiony w punkcie (2,1). O warto

ś

ci pierwszego wiersza lub kolumny decyduje

zmienna ORIGIN.

Sposobem zobrazowania wykresu wektorowego jest utworzenie dwóch tablic
wypełnionymi liczbami. Pierwsza tablica powinna zawiera

ć

współrz

ę

dn

ą

X wektora, a

druga wspórz

ę

dn

ą

Y

ORIGIN

1

≡

M

1

−

3

2

0

2

1

0

1

1

−

















:=

N

3

0

2

0

1

0

1

−

1

−

1

−

















:=

M N

,

(

)