LABORATORIUM METROLOGII
29
.11.2007
Ćwiczenie III: Pomiary czasu częstotliwości i przesunięcia fazowego
Adrian Kajetan Bekasiewicz
EiT 1
album: 108834
1. Obliczyć błąd systematyczny pomiaru korzystając z metody różniczki zupełnej, wiedząc ze błąd
generatora podstawy czasu oscyloskopu wynosi 3%, i przyjmując błąd odczytu ekranu oscyloskopu 1mm.
X
t
[cm]
10
D
tx
[ms/cm] 0,05
F
x
[Hz]
2000
δ
fx
[%]
5
Obliczenia zostały wykonane następująco:
F
x
=
1
D
tx
X
T
⇒
F
x
=
1
10∗10
−
3
∗
0,05
=
2kHz
f
x
=∣
∂
f
x
∂
X
T
X
T
∣∣
∂
f
x
∂
D
tx
D
tx
∣
f
x
=
f
x
f
x
100 %
f
x
=∣
X
T
D
tx
X
T
2
∣∣
D
tx
D
tx
2
X
T
∣
f
x
=
∣
X
T
D
tx
X
T
2
∣∣
D
tx
D
tx
2
X
T
∣
1
D
tx
X
T
100 %=
∣
D
Xt
D
Xt
∣
∣
X
T
X
T
∣
100 %
Po wykonaniu stosownych przekształceń zapisuję :
fx
=
X
T
=
1[mm]oraz
D
tx
D
tx
=
3 %
Po podstawieniu wartości ostatecznie otrzymuję:
fx
=
∣
D
Xt
D
Xt
∣
∣
X
T
X
T
∣
100 %=
1
100
3
100
100 %=4 %
2. Obliczyć maksymalne błędy systematyczne pomiarów. Wyznaczyć błąd względny jako stosunek wartości
obliczonej do teoretycznej. Sprawdzić czy zmierzona wartość mieści się w granicach błędu względem
wartości teoretycznej.
Teoretycznawartość kąta przesunięcia fazowego wynosi :
R=1,021 [k ], C=102,7[nF ] , f =1[kHz]
tg
x
=−
RC , =2 f
=
2 1000=6283,18
rad
s
⇒
tg
x
=−
6283,18∗1021∗102,7∗10
−
9
=−
0,6588
x
=
arctg −0,6588=33
o
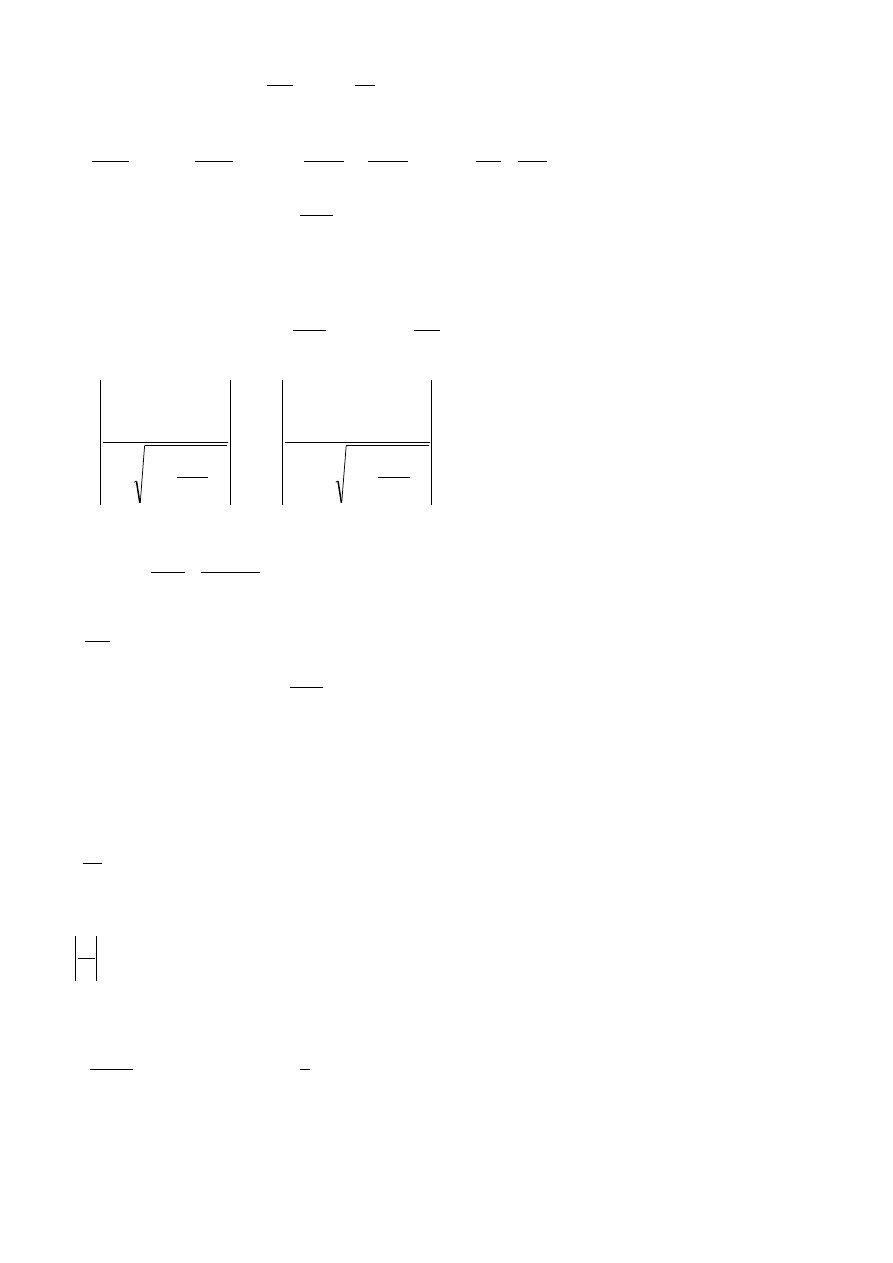
Wartość przesunięcia kąta fazowegodla tablicy 9.2:
=
X
X
T
∗
360
o
=
1
10
∗
360
o
=
36
o
X
=
1 [mm] , X
T
=
1[mm]−błąd odczytu z oscyloskopu
=
∣
∂
∂
X
T
X
T
∣
∣
∂
∂
X
T
X
T
∣
=
∣
X
X
T
∣
∣
X
X
T
2
∣
360
o
=
0,1
10
0,1
100
360
o
=
3,96
o
=
3,96
33
100 %=12 %
∣−
x
∣=
36−33=3
o
Zatem kąt zmierzony mieści się w granicach błędu
Wartość przesunięcia kąta fazowegodla tablicy 9.3:
=±
arcsin
2X
0
2X
m
=±
arcsin
4,4
8
=±
33
o
Maksymalny błąd względny obliczyłem wykorzystując wzór:
(
)
⋅
−
+
⋅
−
±
=
xm
m
m
x
m
m
x
x
x
x
x
x
x
x
ε
ε
ε
ϕ
2
0
2
0
0
2
0
2
2
1
2
2
2
2
1
2
1
W wyniku przeprowadzeniaobliczeń otrzymałem:
max
=
0,1
6,68
0,1∗4,4
53,44
=
0,023≈1,32
o
Wykorzystuję zależność:
%
100
⋅
=
x
x
ϕ
ε
δϕ
ϕ
=
1,32
33
100 %=4 %
∣−
x
∣=
33−33=0
o
Zatem kąt zmierzony mieści się w granicach błędu
4. Obliczyć błąd dyskretyzacji w tablicy 9.5
p
x
T
N
f
=
Błąd dyskretyzacji:
N
1
=
δ
Wynik obliczeń błędu jest procentowy zatem należy otrzymaną wartość pomnożyć przez 100%.
Przykładowe obliczeniadla T
p
=
0,001[ s]:
f
x
=
5
0,001
=
5000 [ Hz]
dyskr.
=
1
5
∗
100 %=20 %
Wyraźnie widać, że błąd dyskretyzacji maleje wraz ze wzrostem liczby pomiarów (co wynika ze wzoru). Przy
małym wypełnieniu licznika błąd dyskretyzacji jest coraz mniejszy i dla N=1 osiąga 100%. Wynika stąd, że
należy tak dobierać warunki pomiaru aby wypełnienie licznika było możliwie największe. Co prowadzi do
minimalizacji błędu dyskretyzacji. Częstotliwość utrzymuje się na stałym poziomie.
5. Wyliczyć i porównać niestabilność generatorów HM 8032 i HM 8031-2.
Celem obliczenia niestabilności względnej generatorów posłużę się wzorem:
f
f
=
f
max
−
f
min
f
nom
Dla HM 8032:
f
f
=
5172,274−5172,244
5000
=
6∗10
−
6
Dla HM 8131−2:
f
f
=
5000,001−5000
5000
=
2∗10
−
7
Analizując choćby rząd wielkości wyników, widać że generator HM 8131-2 ma większą stabilność niż HM 8032.
Spowodowane to jest wpływem warunków zewnętrznych na działanie generatora HM 8032.
6. Na podstawie wzorów podanych w części teoretycznej wyznaczyć częstotliwość generatora na podstawie
pętel epicykloidy i hipocykloidy.
W celu wykonania zadania wykorzystamwzory :
epicykloida :
f
1
f
2
=
1
n1
hipocykloida:
f
1
f
2
=
1
n−1
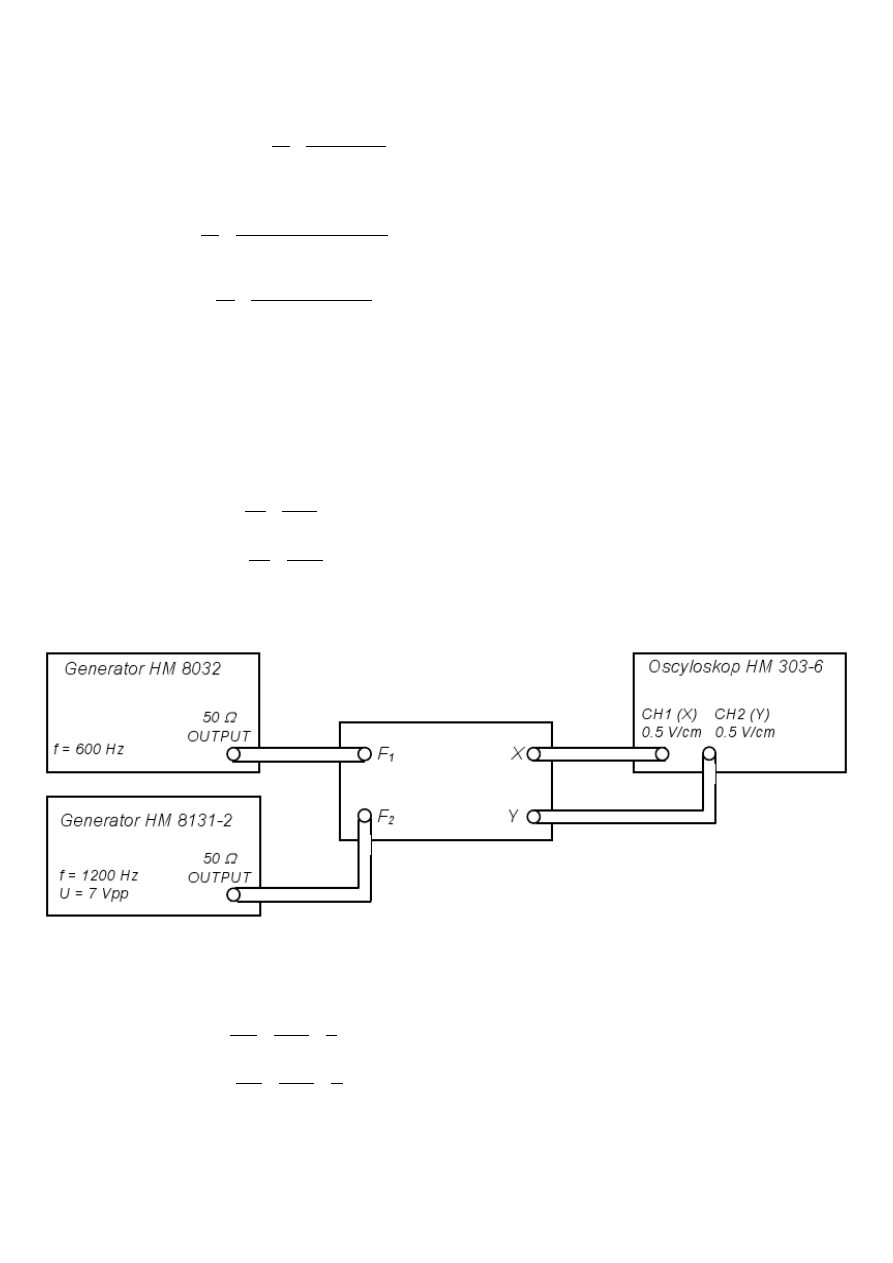
Układ pomiarowy był podłączony jak na rysunku poniżej.
Wartość szukana w obu przypadkach− f
2
:
Znamy wartości dlaepicykloidy f
1e
=
599 [ Hz]oraz dla hipocykloidy f
1h
=
598[ Hz ]
Wykorzystującinformację o liczbie pętli dlaepicykloidy 1, dla hipocykloidy 3 obliczam:
epicykloida :
f
1 e
f
2 e
=
1
11
=
1
2
⇒
f
2 e
=
2f
1e
⇒
f
2 e
=
2∗598=1196[ Hz ]
hipocykloida:
f
1h
f
2h
=
1
3−1
=
1
2
⇒
f
2h
=
2f
1h
⇒
f
2h
=
2∗599=1198 [Hz ]
Wyniki obliczone różnią się nieznacznie od wartości otrzymanych w wyniku pomiaru.
Wyszukiwarka
Podobne podstrony:
cw3 4 odp
PG cw3
Klucz odp W strone matury[1]
fizyka 1 odp (3)
zestaw14 odp
2009 ODP
Analiza 2, am2 e efgh6 odp[1]
matematyka 2 odp (4)
odp 108 143 id 331974 Nieznany
Prawo handlowe pytania odp
cw3
cw3 rezystancja id 123348 Nieznany
pozostale odp bankowosc id 3805 Nieznany
odp matematyka 2
cw3 2014 notatki
więcej podobnych podstron