Projekt
nr 1 - Poz. 1.1 strona nr
|
|
|
CHARAKTERYSTYKA WARUNKÓW PODPARCIA UKŁADU |
|
|
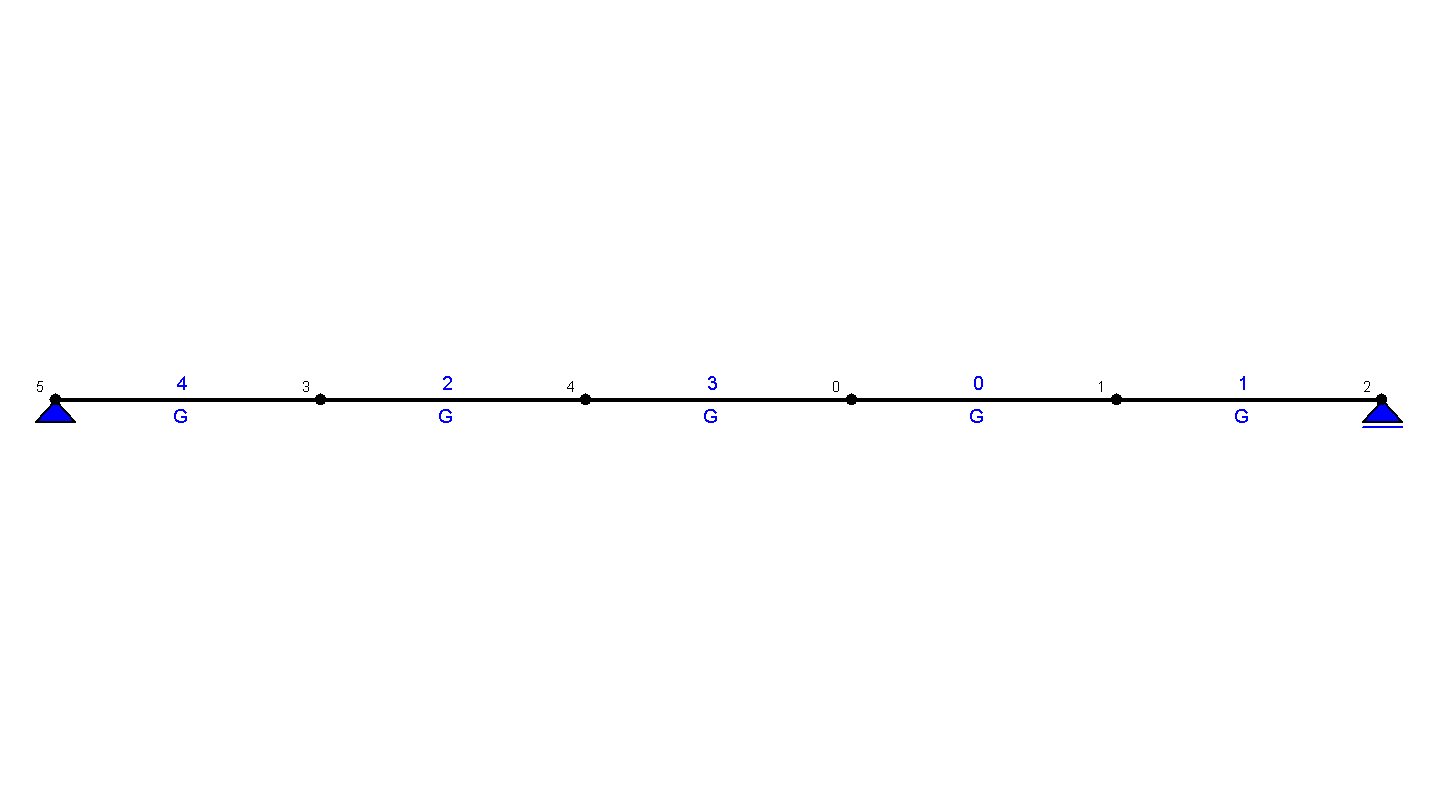
Charakterystyka podpór układu
|
|
Nr |
Węzeł |
Typ |
Kąt [st] |
Podatność x [m/kN] |
Podatność y [m/kN] |
Podatność kątowa [rad/kNm] |
|
|
|
0 |
5 |
Nieprzesuwna |
0.00 |
0.0000 |
0.0000 |
---- |
|
|
|
1 |
2 |
Przesuwna |
0.00 |
0.0000 |
0.0000 |
---- |
|
Informacje związane z wymuszeniami podpór układu
|
|
Nr |
Wymuszenie x [m] |
Wymuszenie y [m] |
Wymuszenie kątowe [rad] |
|
|
|
0 |
0.0000 |
0.0000 |
---- |
|
|
|
1 |
0.0000 |
0.0000 |
---- |
|
UWAGA! Wartości związane z podatnością i wymuszeniami podpór określone są w lokalnych układach współrzędnych poszczególnych podpór.
|
|
|
CHARAKTERYSTYKA OBCIĄŻENIA UKŁADU |
|
|
Charakterystyka grup obciążeń
|
Nr |
Nazwa |
Typ |
I/O |
Min |
Max |
Psi d |
Ranga |
Opis |
|
0 |
Wymuszenia układu |
ZMIENNE |
AKTYWNE |
1.00 |
1.00 |
1.00 |
1 |
Osiadanie podpór układu. |
|
1 |
Ciężar własny konstrukcji |
STALE |
AKTYWNE |
1.00 |
1.00 |
1.00 |
1 |
Obciążenie ciężarem własnym. |
|
2 |
Obciążenia podstawowe |
ZMIENNE |
AKTYWNE |
1.00 |
1.00 |
1.00 |
1 |
Obciążenia podstawowe układu. |
Charakterystyka sił związanych z wszystkimi grupami obciążenia
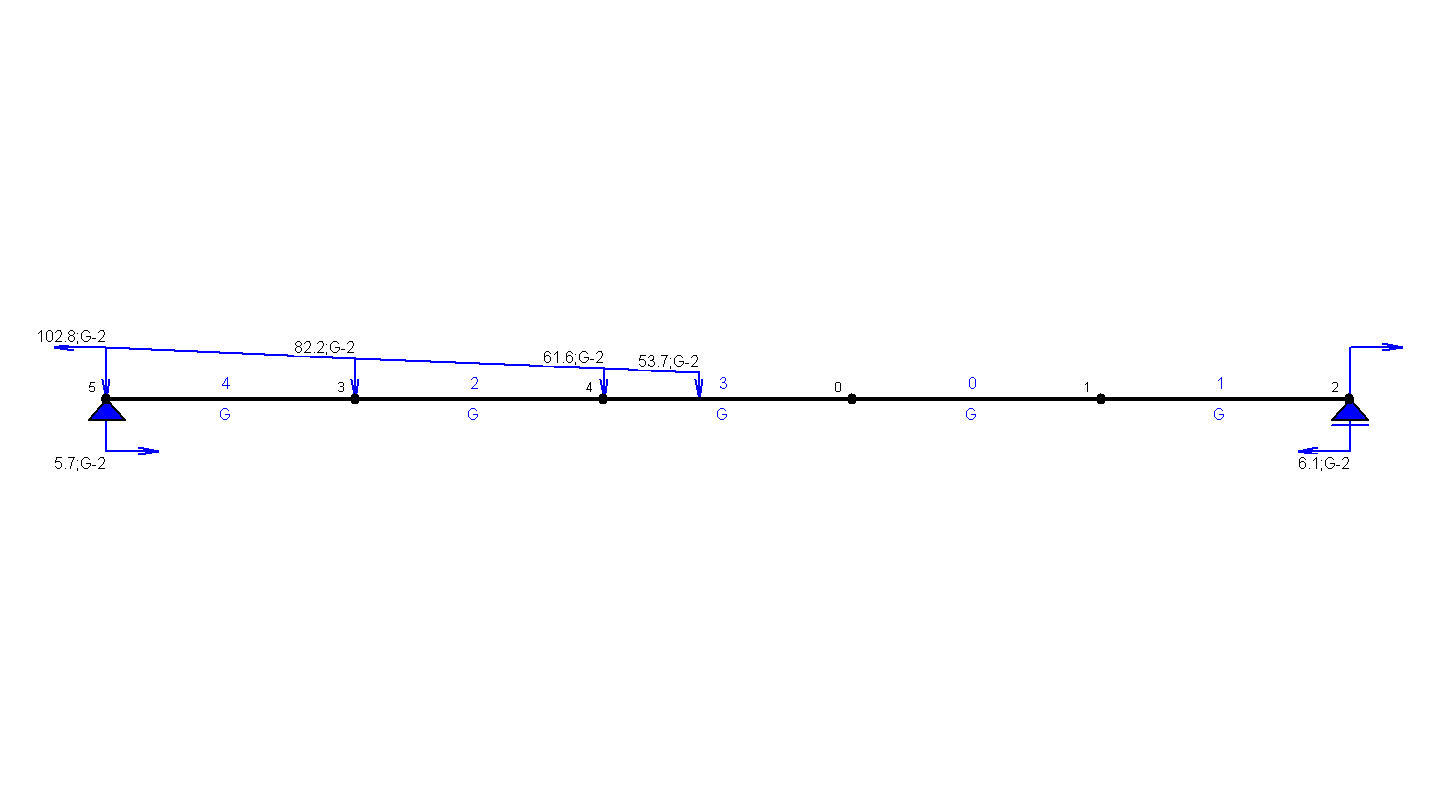
|
Nr |
Pręt |
Typ |
Kąt [st] |
S1 [m] |
S2 [m] |
W1 [kN(m)] |
W2 [kN(m)] |
Tg [K] |
Td [K] |
|
0 |
4 |
Mom. skupiony |
---- |
0.000 |
---- |
-5.680 |
---- |
---- |
---- |
|
1 |
1 |
Mom. skupiony |
---- |
0.524 |
---- |
6.064 |
---- |
---- |
---- |
|
2 |
4 |
Liniowe X |
0.00 |
0.000 |
0.524 |
102.750 |
82.200 |
---- |
---- |
|
3 |
2 |
Liniowe X |
0.00 |
0.000 |
0.524 |
82.200 |
61.650 |
---- |
---- |
|
4 |
3 |
Liniowe X |
0.00 |
0.000 |
0.202 |
61.650 |
53.730 |
---- |
---- |
Uwzględnienie ciężaru własnego
|
|
Pręt |
Grawitacja |
|
|
|
0 |
UWZGLĘDNIONO |
|
|
|
1 |
UWZGLĘDNIONO |
|
|
|
2 |
UWZGLĘDNIONO |
|
|
|
3 |
UWZGLĘDNIONO |
|
|
|
4 |
UWZGLĘDNIONO |
|
UWAGA! Obciążenie ciężarem własnym jest automatycznie przypisywane do grupy obciążenia: "Ciezar wlasny konstrukcji".
|
|
|
WYNIKI DLA KOMBINATORYKI OBCIĄŻEŃ |
|
|
Charakterystyka grup obciążeń
|
Nr |
Nazwa |
Typ |
I/O |
Min |
Max |
Psi d |
Ranga |
Opis |
|
0 |
Wymuszenia układu |
ZMIENNE |
AKTYWNE |
1.00 |
1.00 |
1.00 |
1 |
Osiadanie podpór układu. |
|
1 |
Ciężar własny konstrukcji |
STALE |
AKTYWNE |
1.00 |
1.00 |
1.00 |
1 |
Obciążenie ciężarem własnym. |
|
2 |
Obciążenia podstawowe |
ZMIENNE |
AKTYWNE |
1.00 |
1.00 |
1.00 |
1 |
Obciążenia podstawowe układu. |
Obliczenia (kombinatorykę) przeprowadzono dla obciążeń OBLICZENIOWYCH
Efekty działania obciążeń z grup o statusie "stałe" są uwzględniane zawsze, natomiast z grup o statusie "zmienne" tylko wtedy, gdy wpływają na zwiększenie lub zmniejszenie wartości finalnej odpowiednio do poszukiwanego ekstremum.
Jeżeli uwzględniane są wartości obliczeniowe obciążenia to sumowanie wartości cząstkowych będących efektem działania obciążeń zarówno stałych jak i zmiennych, odbywa się przy uwzględnieniu odpowiedniego współczynnika obciążenia.
W sumowaniu nie uwzględnia się efektów wynikłych z działania obciążenia z grup NIEAKTYWNYCH.
Charakterystyka relacji między grupami obciążenia
|
Nr |
Typ |
Grupy |
|
0 |
LUB |
0;1;2; |
Grupy relacji określają możliwości i zasady kojarzenia skutków związanymi z poszczególnymi schematami obciążenia. Efekty wywołane grupami zawartymi w relacji typu "LUB", kojarzone są dowolnie z uwzględnieniem faktu stałości lub zmienności obciążenia. Relacja typu "ALBO", umożliwia natomiast wybranie jednej ze zdefiniowanych w niej grup, której efekt najmocniej wpływa na ekstremalizację poszukiwanej wartości.
|
|
|
OBWIEDNIA SIŁ PRZEKROJOWYCH - NORMALNE [kN] |
|
|
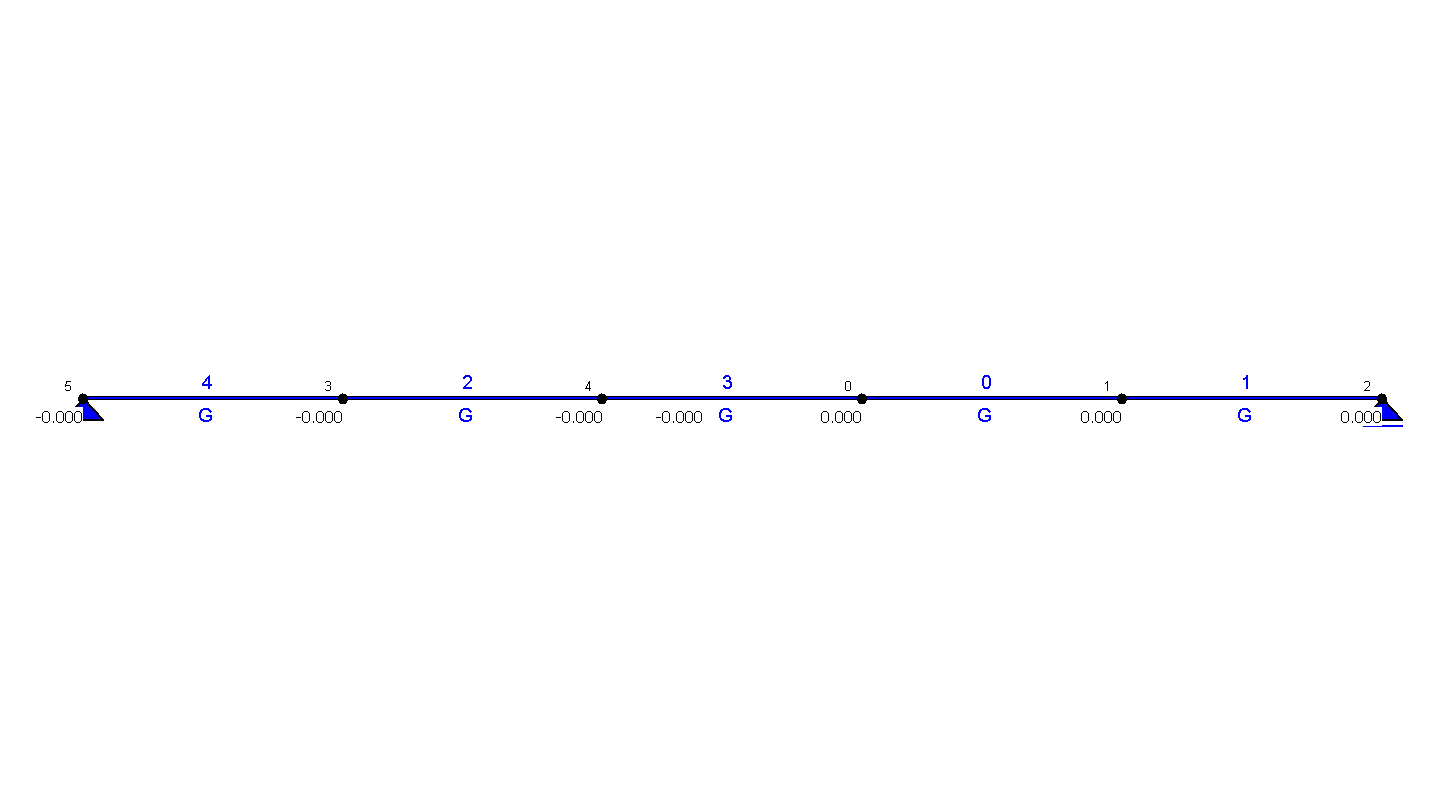
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
|
|
|
OBWIEDNIA SIŁ PRZEKROJOWYCH - TNĄCE [kN] |
|
|
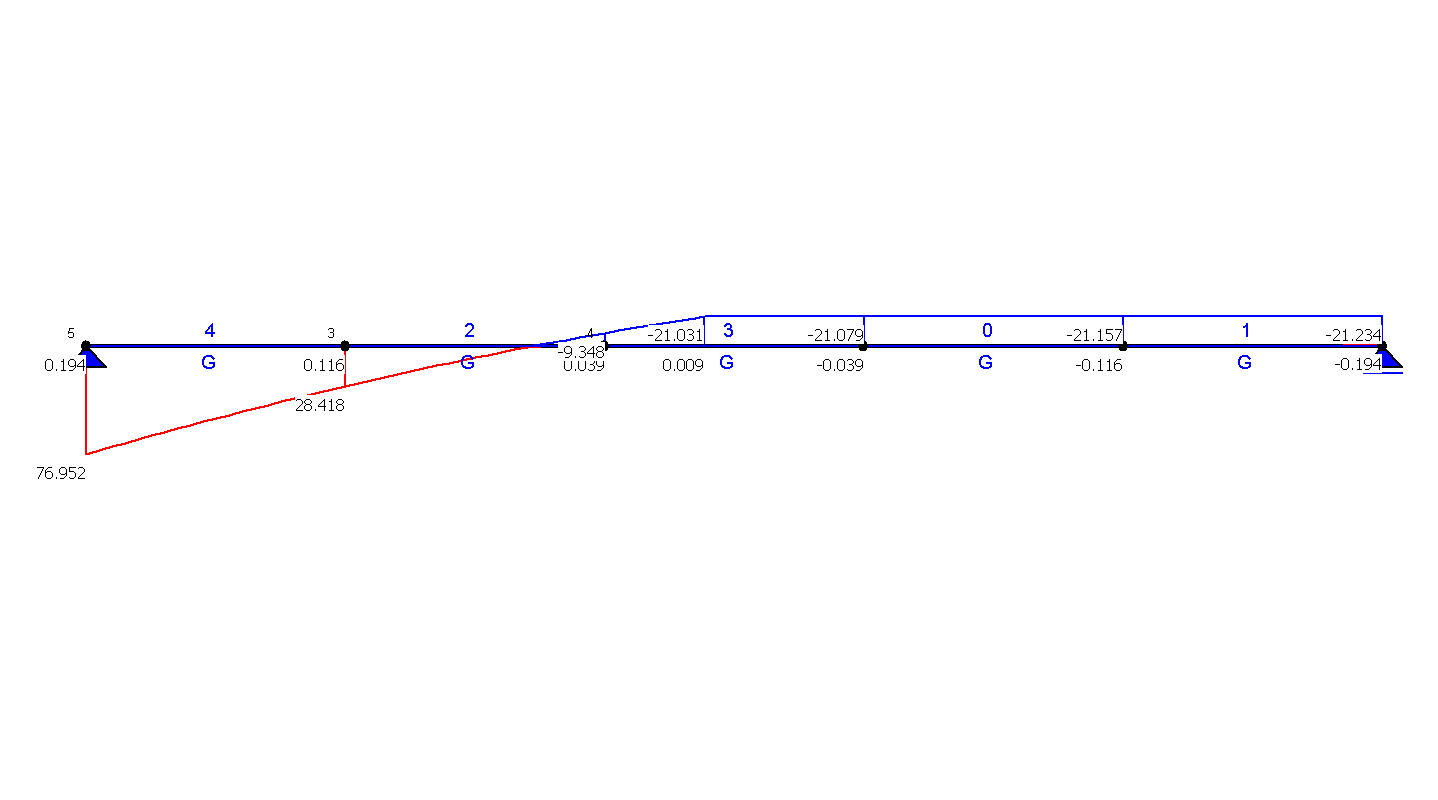
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
|
|
|
OBWIEDNIA SIŁ PRZEKROJOWYCH - MOMENTY ZGINAJĄCE [kNm] |
|
|
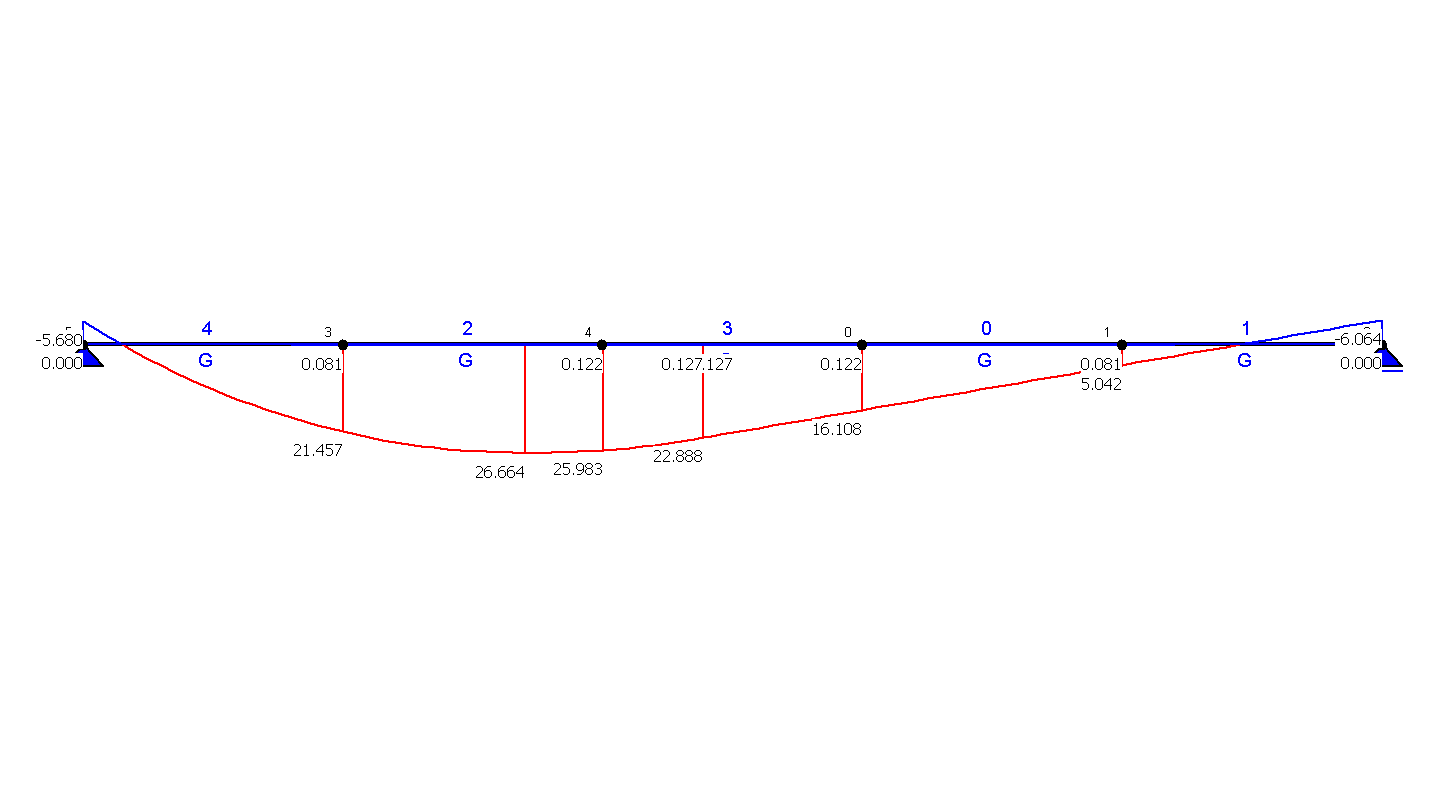
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
|
|
|
WARTOŚCI SIŁ PRZEKROJOWYCH - KOMBINATORYKA |
|
|
Zestawienie tabelaryczne wartości sił przekrojowych w charakterystycznych punktach
|
Pręt |
x/L |
N [kN] |
T [kN] |
M [kNm] |
Grupy |
|
0 |
0.000 |
*0.000* |
-0.039 |
0.122 |
-1; |
|
|
0.000 |
0.000 |
*-21.079* |
16.108 |
1;2; |
|
|
0.000 |
0.000 |
-0.039 |
*0.122* |
-1; |
|
|
0.000 |
*0.000* |
-21.079 |
16.108 |
1;2; |
|
|
0.000 |
0.000 |
*-0.039* |
0.122 |
-1; |
|
|
0.000 |
0.000 |
-21.079 |
*16.108* |
1;2; |
|
|
1.000 |
*0.000* |
-0.116 |
0.081 |
-1; |
|
|
1.000 |
0.000 |
*-21.157* |
5.042 |
1;2; |
|
|
1.000 |
0.000 |
-0.116 |
*0.081* |
-1; |
|
|
1.000 |
*0.000* |
-21.157 |
5.042 |
1;2; |
|
|
1.000 |
0.000 |
*-0.116* |
0.081 |
-1; |
|
|
1.000 |
0.000 |
-21.157 |
*5.042* |
1;2; |
|
1 |
0.000 |
*0.000* |
-0.116 |
0.081 |
-1; |
|
|
0.000 |
0.000 |
*-21.157* |
5.042 |
1;2; |
|
|
0.000 |
0.000 |
-0.116 |
*0.081* |
-1; |
|
|
0.000 |
*0.000* |
-21.157 |
5.042 |
1;2; |
|
|
0.000 |
0.000 |
*-0.116* |
0.081 |
-1; |
|
|
0.000 |
0.000 |
-21.157 |
*5.042* |
1;2; |
|
|
1.000 |
*0.000* |
-0.194 |
0.000 |
-1; |
|
|
1.000 |
0.000 |
*-21.234* |
0.000 |
1;2; |
|
|
1.000 |
0.000 |
-0.194 |
*0.000* |
-1; |
|
|
1.000 |
*0.000* |
-21.234 |
0.000 |
1;2; |
|
|
1.000 |
0.000 |
*-0.194* |
0.000 |
-1; |
|
|
1.000 |
0.000 |
-21.234 |
*0.000* |
1;2; |
|
2 |
0.000 |
*-0.000* |
28.418 |
21.457 |
1;2; |
|
|
0.000 |
-0.000 |
*0.116* |
0.081 |
-1; |
|
|
0.000 |
-0.000 |
0.116 |
*0.081* |
-1; |
|
|
0.000 |
*-0.000* |
0.116 |
0.081 |
-1; |
|
|
0.000 |
-0.000 |
*28.418* |
21.457 |
1;2; |
|
|
0.000 |
-0.000 |
28.418 |
*21.457* |
1;2; |
|
|
1.000 |
*-0.000* |
0.039 |
0.122 |
1; |
|
|
1.000 |
0.000 |
*-9.348* |
25.983 |
-1;2; |
|
|
1.000 |
-0.000 |
0.039 |
*0.122* |
-1; |
|
|
1.000 |
*0.000* |
-9.348 |
25.983 |
-1;2; |
|
|
1.000 |
-0.000 |
*0.039* |
0.122 |
1; |
|
|
1.000 |
0.000 |
-9.348 |
*25.983* |
1;2; |
|
|
0.700 |
*-0.000* |
0.851 |
26.664 |
1;2; |
|
|
0.700 |
-0.000 |
*0.062* |
0.114 |
-1; |
|
|
0.700 |
-0.000 |
0.062 |
*0.114* |
-1; |
|
|
0.700 |
*-0.000* |
0.062 |
0.114 |
-1; |
|
|
0.700 |
-0.000 |
*0.851* |
26.664 |
1;2; |
|
|
0.700 |
-0.000 |
0.851 |
*26.664* |
1;2; |
|
3 |
0.000 |
*-0.000* |
0.039 |
0.122 |
1; |
|
|
0.000 |
0.000 |
*-9.348* |
25.983 |
-1;2; |
|
|
0.000 |
-0.000 |
0.039 |
*0.122* |
-1; |
|
|
0.000 |
*0.000* |
-9.348 |
25.983 |
-1;2; |
|
|
0.000 |
-0.000 |
*0.039* |
0.122 |
1; |
|
|
0.000 |
0.000 |
-9.348 |
*25.983* |
1;2; |
|
|
0.386 |
*-0.000* |
0.009 |
0.127 |
1; |
|
|
0.386 |
0.000 |
*-21.031* |
22.888 |
-1;2; |
|
|
0.386 |
-0.000 |
0.009 |
*0.127* |
-1; |
|
|
0.386 |
*0.000* |
-21.031 |
22.888 |
-1;2; |
|
|
0.386 |
-0.000 |
*0.009* |
0.127 |
1; |
|
|
0.386 |
0.000 |
-21.031 |
*22.888* |
1;2; |
|
|
1.000 |
*0.000* |
-0.039 |
0.122 |
-1; |
|
|
1.000 |
0.000 |
*-21.079* |
16.108 |
1;2; |
|
|
1.000 |
0.000 |
-0.039 |
*0.122* |
-1; |
|
|
1.000 |
*0.000* |
-21.079 |
16.108 |
1;2; |
|
|
1.000 |
0.000 |
*-0.039* |
0.122 |
-1; |
|
|
1.000 |
0.000 |
-21.079 |
*16.108* |
1;2; |
|
|
0.500 |
*0.000* |
-0.000 |
0.127 |
-1; |
|
|
0.500 |
0.000 |
*-21.040* |
21.626 |
1;2; |
|
|
0.500 |
0.000 |
-0.000 |
*0.127* |
-1; |
|
|
0.500 |
*0.000* |
-21.040 |
21.626 |
1;2; |
|
|
0.500 |
0.000 |
*-0.000* |
0.127 |
-1; |
|
|
0.500 |
0.000 |
-21.040 |
*21.626* |
1;2; |
|
4 |
0.000 |
*-0.000* |
76.953 |
-5.680 |
1;2; |
|
|
0.000 |
-0.000 |
*0.194* |
0.000 |
-1; |
|
|
0.000 |
-0.000 |
76.953 |
*-5.680* |
-1;2; |
|
|
0.000 |
*-0.000* |
0.194 |
0.000 |
-1; |
|
|
0.000 |
-0.000 |
*76.953* |
-5.680 |
1;2; |
|
|
0.000 |
-0.000 |
0.194 |
*0.000* |
1; |
|
|
1.000 |
*-0.000* |
28.418 |
21.457 |
1;2; |
|
|
1.000 |
-0.000 |
*0.116* |
0.081 |
-1; |
|
|
1.000 |
-0.000 |
0.116 |
*0.081* |
-1; |
|
|
1.000 |
*-0.000* |
0.116 |
0.081 |
-1; |
|
|
1.000 |
-0.000 |
*28.418* |
21.457 |
1;2; |
|
|
1.000 |
-0.000 |
28.418 |
*21.457* |
1;2; |
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
UWAGA!!! Wartości wyróżnione symbolem '*' oznaczają ekstremalne wartości dla danego punktu.
|
|
|
KOMBINATORYKA OBCIĄŻEŃ - NAPRĘŻENIA NORMALNE |
|
|
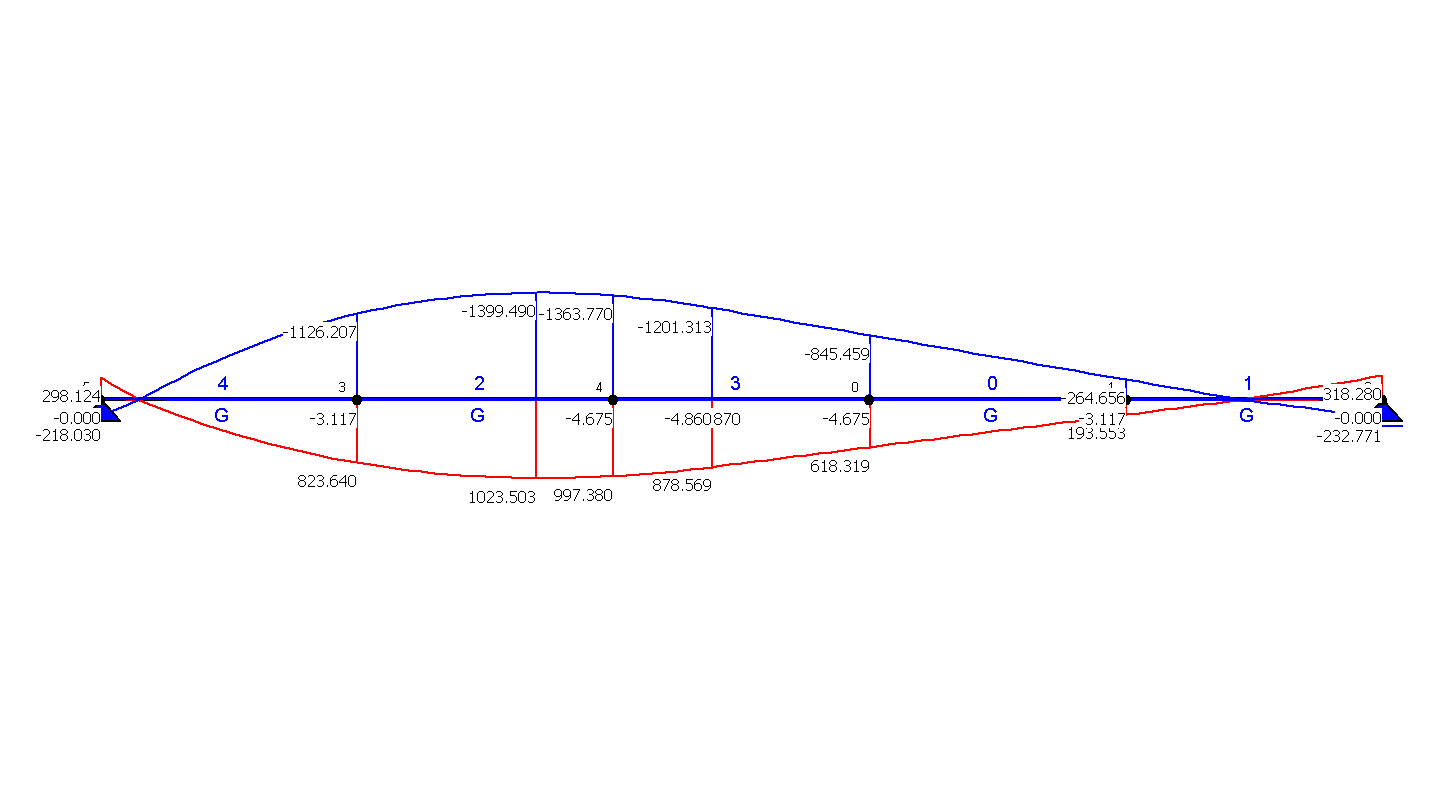
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
|
|
|
WARTOŚCI NAPRĘŻEŃ NORMALNYCH - KOMBINATORYKA |
|
|
Zestawienie tabelaryczne wartości naprężeń normalnych w charakterystycznych punktach
|
Pręt |
x/L |
nXg [MPa] |
nXd [MPa] |
Grupy |
|
0 |
0.000 |
*-845.460* |
618.319 |
1;2; |
|
|
0.000 |
-6.393 |
*4.675* |
-1; |
|
|
0.000 |
*-6.393* |
4.675 |
-1; |
|
|
0.000 |
-845.460 |
*618.319* |
1;2; |
|
|
1.000 |
*-264.655* |
193.553 |
1;2; |
|
|
1.000 |
-4.262 |
*3.117* |
-1; |
|
|
1.000 |
*-4.262* |
3.117 |
-1; |
|
|
1.000 |
-264.655 |
*193.553* |
1;2; |
|
1 |
0.000 |
*-264.655* |
193.553 |
1;2; |
|
|
0.000 |
-4.262 |
*3.117* |
-1; |
|
|
0.000 |
*-4.262* |
3.117 |
-1; |
|
|
0.000 |
-264.655 |
*193.553* |
1;2; |
|
|
1.000 |
*0.000* |
0.000 |
-1; |
|
|
1.000 |
0.000 |
*0.000* |
-1; |
|
|
1.000 |
*0.000* |
0.000 |
1;2; |
|
|
1.000 |
0.000 |
*0.000* |
1;2; |
|
2 |
0.000 |
*-1126.206* |
823.640 |
1;2; |
|
|
0.000 |
-4.262 |
*3.117* |
-1; |
|
|
0.000 |
*-4.262* |
3.117 |
-1; |
|
|
0.000 |
-1126.206 |
*823.640* |
1;2; |
|
|
1.000 |
*-1363.770* |
997.380 |
1;2; |
|
|
1.000 |
-6.393 |
*4.675* |
-1; |
|
|
1.000 |
*-6.393* |
4.675 |
-1; |
|
|
1.000 |
-1363.770 |
*997.380* |
1;2; |
|
|
0.700 |
*-1399.490* |
1023.503 |
1;2; |
|
|
0.700 |
-5.977 |
*4.371* |
-1; |
|
|
0.700 |
*-5.977* |
4.371 |
-1; |
|
|
0.700 |
-1399.490 |
*1023.503* |
1;2; |
|
3 |
0.000 |
*-1363.770* |
997.380 |
1;2; |
|
|
0.000 |
-6.393 |
*4.675* |
-1; |
|
|
0.000 |
*-6.393* |
4.675 |
-1; |
|
|
0.000 |
-1363.770 |
*997.380* |
1;2; |
|
|
0.386 |
*-1201.308* |
878.565 |
1;2; |
|
|
0.386 |
-6.645 |
*4.860* |
-1; |
|
|
0.386 |
*-6.645* |
4.860 |
-1; |
|
|
0.386 |
-1201.308 |
*878.565* |
1;2; |
|
|
1.000 |
*-845.460* |
618.319 |
1;2; |
|
|
1.000 |
-6.393 |
*4.675* |
-1; |
|
|
1.000 |
*-6.393* |
4.675 |
-1; |
|
|
1.000 |
-845.460 |
*618.319* |
1;2; |
|
|
0.500 |
*-1135.063* |
830.118 |
1;2; |
|
|
0.500 |
-6.659 |
*4.870* |
-1; |
|
|
0.500 |
*-6.659* |
4.870 |
-1; |
|
|
0.500 |
-1135.063 |
*830.118* |
1;2; |
|
4 |
0.000 |
*-0.000* |
-0.000 |
1; |
|
|
0.000 |
298.126 |
*-218.031* |
1;2; |
|
|
0.000 |
*298.126* |
-218.031 |
-1;2; |
|
|
0.000 |
-0.000 |
*-0.000* |
-1; |
|
|
1.000 |
*-1126.206* |
823.640 |
1;2; |
|
|
1.000 |
-4.262 |
*3.117* |
-1; |
|
|
1.000 |
*-4.262* |
3.117 |
-1; |
|
|
1.000 |
-1126.206 |
*823.640* |
1;2; |
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
UWAGA!!! Wartości wyróżnione symbolem '*' oznaczają ekstremalne wartości dla danego punktu.
|
|
|
KOMBINATORYKA OBCIĄŻEŃ - REAKCJE PODPOROWE |
|
|
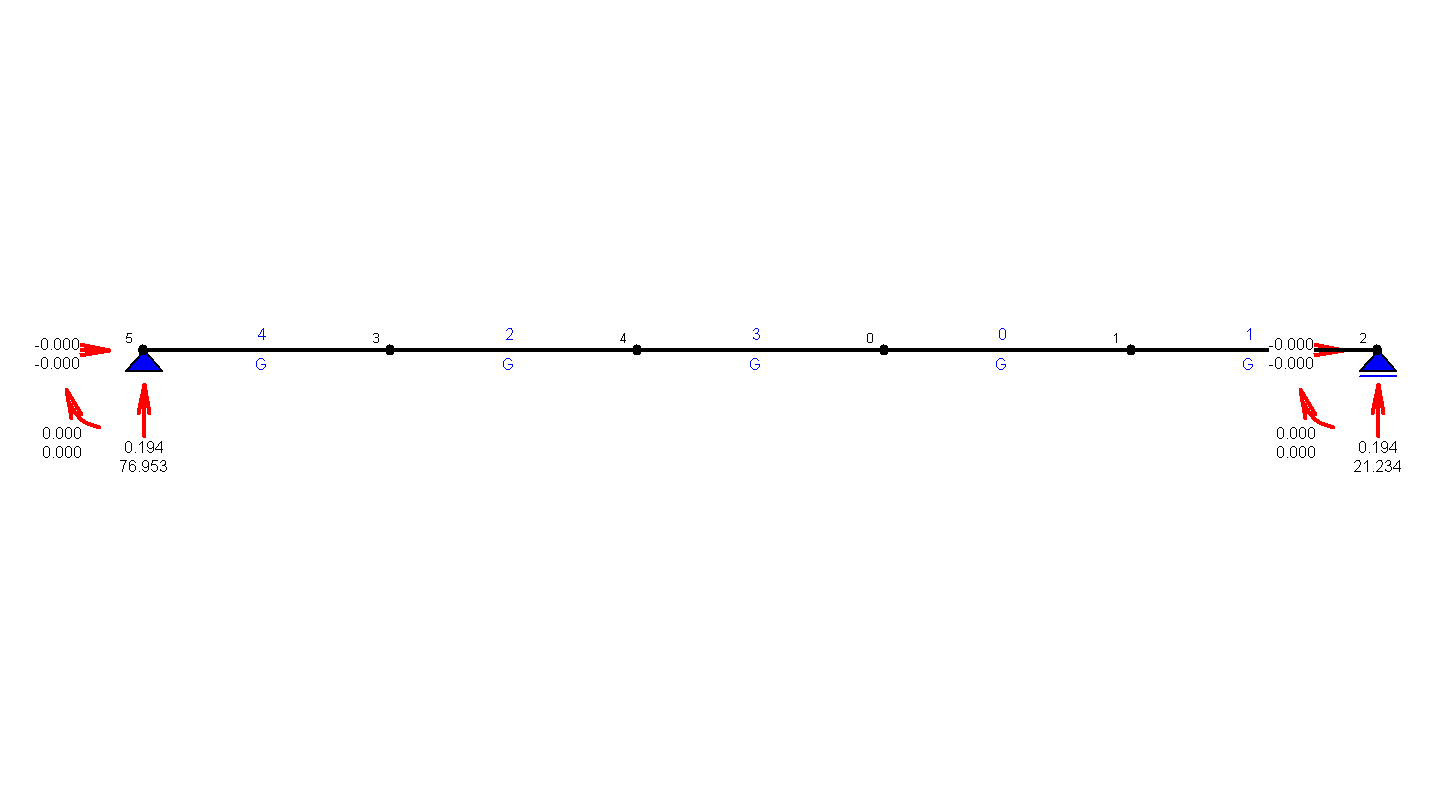
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
Tabela maksymalnych/minimalnych reakcji podporowych układu
|
Numer |
Węzeł |
min Rx [kN] |
min Ry [kN] |
min R [kN] |
min M [kNm] |
max Rx [kN] |
max Ry [kN] |
max R [kN] |
max M [kNm] |
|
0 |
5 |
-0.00 |
0.19 |
0.19 |
0.00 |
-0.00 |
76.95 |
76.95 |
0.00 |
|
1 |
2 |
-0.00 |
0.19 |
0.19 |
0.00 |
-0.00 |
21.23 |
21.23 |
0.00 |
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
|
|
|
KOMBINATORYKA OBCIĄŻEŃ - DEFORMACJE UKŁADU |
|
|
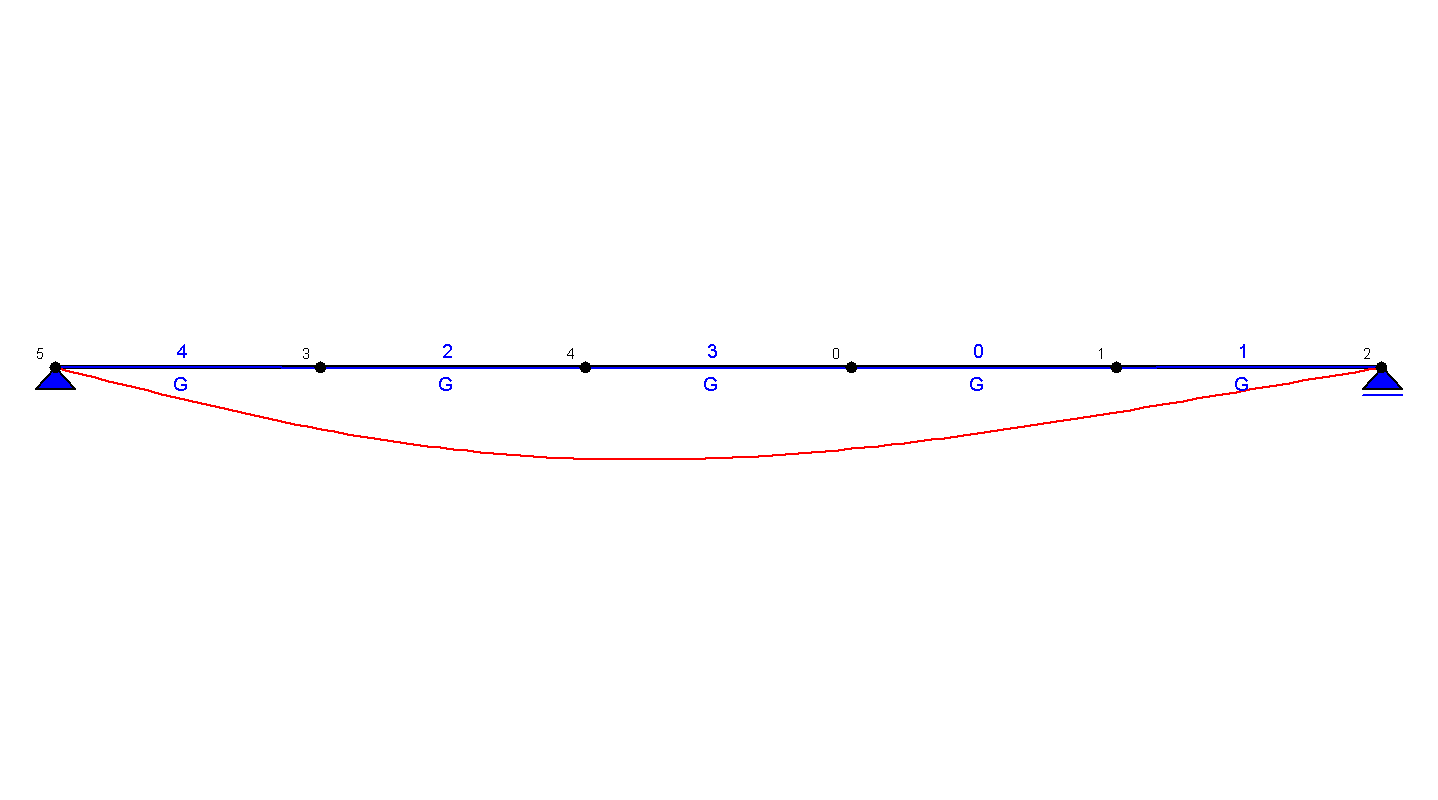
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
|
|
|
WARTOŚCI EKSTREMALNYCH PRZEMIESZCZEŃ LOKALNYCH - KOMBINATORYKA |
|
|
Zestawienie tabelaryczne ekstremalnych przemieszczeń lokalnych w charakterystycznych punktach
|
Pręt |
x/L |
min u [cm] |
min v [cm] |
min fi [st] |
max u [cm] |
max v [cm] |
max fi [st] |
|
0 |
0.000 |
-0.00000 |
0.03618 |
-2.03824 |
-0.00000 |
5.73610 |
-0.00787 |
|
|
1.000 |
-0.00000 |
0.02256 |
-3.36833 |
-0.00000 |
3.15776 |
-0.02106 |
|
1 |
0.000 |
-0.00000 |
0.02256 |
-3.36833 |
-0.00000 |
3.15776 |
-0.02106 |
|
|
1.000 |
0.00000 |
0.00000 |
-3.30452 |
0.00000 |
0.00000 |
-0.02659 |
|
2 |
0.000 |
-0.00000 |
0.02256 |
0.02106 |
-0.00000 |
4.35741 |
3.85202 |
|
|
1.000 |
-0.00000 |
0.03618 |
0.00787 |
-0.00000 |
6.46416 |
0.66226 |
|
|
0.700 |
-0.00000 |
0.03340 |
0.01233 |
-0.00000 |
6.14614 |
1.66022 |
|
3 |
0.000 |
-0.00000 |
0.03618 |
0.00787 |
-0.00000 |
6.46416 |
0.66226 |
|
|
0.386 |
-0.00000 |
0.03790 |
-0.53167 |
-0.00000 |
6.48276 |
0.00183 |
|
|
1.000 |
-0.00000 |
0.03618 |
-2.03824 |
-0.00000 |
5.73610 |
-0.00787 |
|
|
0.500 |
-0.00000 |
0.03799 |
-0.85209 |
-0.00000 |
6.41015 |
0.00000 |
|
4 |
0.000 |
0.00000 |
0.00000 |
0.02659 |
0.00000 |
0.00000 |
5.11034 |
|
|
1.000 |
-0.00000 |
0.02256 |
0.02106 |
-0.00000 |
4.35741 |
3.85202 |
UWAGA!!! Prezentowane wyniki zostały obliczone dla : Kombinatoryka obciążeń (SGN - Kombinacja podstawowa)
Raport
wygenerowany programem Soldis v4.2
Licencja:
Edukacyjna
Wyszukiwarka
Podobne podstrony:
Budownictwo Ogólne 2 - Projekt - przykład 2, Pozycja obliczeniowa nr 4, Obliczenia ław fundamentowyc
Lab 05 Obliczenia w C id 257534 Nieznany
Algorytmy obliczen id 57749 Nieznany
Oblicz (2) id 327340 Nieznany
platew obliczenia id 343774 Nieznany
Różne oblicza wsi w literaturze polskiej, prezentacje
Podstawy analizy fundamentalnej Nieznany
obliczenia wytrzymalosciowe id Nieznany
OBLICZENIA ZAPOTRZEBOWANIA CIEP Nieznany
Różne obliczenia, Dach drewniany płatwiowo-kleszczowy, 6
Prawdziwe oblicze zydostwa id 3 Nieznany
Przedstaw różne oblicza młodości w literaturze XIX wieku
1 Milosc rozne oblicza PLANSZE milosc w
Różne obliczenia, SCIANY2, A=(a1+a2)x0,5+a3=3,7[m
Różne obliczenia, Dokumentacja Budynku, Opis techniczny:
Różne obliczenia, STROPY1, 1