POCHODNA
Pojęcie pochodnej funkcji jest podstawowym pojęciem analizy matematycznej i ma szerokie zastosowania. Definicję pochodnej podali niezależnie od siebie Newton, w związku z rozważaniami dotyczącymi prędkości ruchu punktu materialnego, oraz Leibniz, przy rozpatrywaniu zagadnienia stycznej do krzywej.
Definicja.
Niech dana będzie funkcja f : A→R, A⊂R. Jeżeli istnieje granica skończona
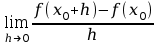
to granicę tę nazywamy pochodną funkcji f w punkcie x0 i oznaczamy najczęściej symbolem f ’(x0).
Iloraz
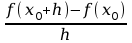
przyrostu wartości funkcji do przyrostu argumentu nazywamy ilorazem różnicowym funkcji.
Wzory na pochodne wybranych funkcji znajdują się w dołączonej tablicy.
I. Interpretacja geometryczna. Równanie stycznej
Jeżeli funkcja f jest ciągła w punkcie x0 i ma w tym punkcie pochodną f ’(x0), to do wykresu tej funkcji istnieje w punkcie (x0, f(x0)) styczna o równaniu
y-f(x0)=f ’(x0)(x- x0).
Styczna ta jest granicą siecznych przechodzących przez punkty A(x0, f(x0)) oraz
B(x0+h, f(x0+h)) przy h zmierzającym do 0. Fakt ten ilustruje poniższy rysunek.
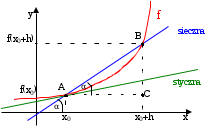
Długość odcinka BC jest równa przyrostowi wartości funkcji f odpowiadającego przyrostowi argumentu o h (długość odcinka AC). Iloraz różnicowy funkcji jest więc stosunkiem długości odcinków BC do AC. Jest on zatem równy tangensowi kąta α nachylenia siecznej AB do osi OX, co oznacza, że w sensie geometrycznym jest on równy współczynnikowi kierunkowemu siecznej AB.
Jeżeli przyrost argumentu h maleje do zera, to punkt B zbliża się do punktu A. Przy przejściu do granicy (czyli do pochodnej) punkt ten pokryje się z punktem A, a sieczna stanie się już styczną (im mniejszy przyrost argumentu h, tym bardziej sieczne zbliżają się do stycznej). Zatem pochodną w punkcie x0 możemy interpretować geometrycznie jako współczynnik kierunkowy stycznej do wykresu funkcji f w punkcie o współrzędnych (x0, f(x0)).
Przykład.
Wyznaczymy równanie stycznej do wykresu funkcji f(x)=3x2-5 w punkcie A(1,-2).
Zauważmy od razu, że x0=1 i f(x0)=f(1)=-2. Aby skorzystać z podanego wzoru stycznej, brakuje nam tylko wartości f’(1). W tym celu policzmy pochodną
f’(x)= 6x oraz f’(1)= 6∙1=6.
Na podstawie podanego wzoru stycznej otrzymujemy
y-(-2)=6(x-1)
czyli równane stycznej do funkcji w punkcie A(1,-2) ma postać
y=6x-8
II. Monotoniczność funkcji
Jednym z najważniejszych zastosowań pochodnej funkcji jest badanie i wyznaczanie monotoniczności funkcji oraz wyznaczanie jej największej i najmniejszej wartości (w całej dziedzinie, lub jej podzbiorze). Badanie monotoniczności funkcji za pomocą pochodnych opiera się na następującym twierdzeniu Lagrange’a.
TWIERDZENIE Lagrange’a
Jeżeli funkcja f jest ciągła w przedziale domkniętym [a, b] i różniczkowalna wewnątrz tego przedziału, to istnieje taki punkt c∊(a, b), że
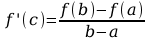
Wartość f’(c) interpretujemy jako średnią szybkość zmian wartości f(x) w przedziale [a, b]. Dlatego też twierdzenie to nosi nazwę twierdzenia o wartości średniej, lub twierdzenia o przyrostach.
Wnioski z tego twierdzenia są następujące:
1. Jeżeli pochodna funkcji f jest równa zero w każdym punkcie przedziału (a, b) to funkcja f jest stała w tym przedziale.
2. Jeżeli pochodna funkcji f jest dodatnia w każdym punkcie przedziału (a, b) to funkcja f jest w tym przedziale rosnąca.
3. Jeżeli pochodna funkcji f jest ujemna w każdym punkcie przedziału (a, b) to funkcja f jest w tym przedziale malejąca.
Przykład.
Zbadamy monotoniczność funkcji f(x) = 4+3x2-x3.
Funkcja ta jako funkcja wielomianowa jest różniczkowalna. Policzmy jej pochodną i zbadajmy jej znak.
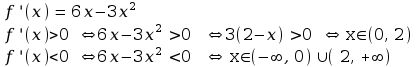
Zatem funkcja rośnie w przedziale (0, 2), natomiast maleje w przedziałach (-∞, 0) i (2,∞).
III. Ekstrema lokalne funkcji
Drugim bardzo ważnym zastosowaniem pochodnej funkcji jest wyznaczanie ekstremów lokalnych funkcji. Ekstremami lokalnymi funkcji nazywamy maksima i minima lokalne funkcji.
Mówimy, że funkcja f ma w punkcie x0 maksimum (minimum) lokalne równe f(x0), jeżeli istnieje takie otoczenie (x0-δ, x0+δ) punktu x0, że dla każdego x∊(x0-δ, x0+δ) zachodzi nierówność
f(x)≤
f(x0)
( f(x)≥ f(x0)
)
Powyższe określenia ilustrują rysunki.
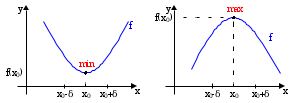
Pojęcie ekstremum funkcji w punkcie jest pojęciem lokalnym odnoszącym się do małego otoczenia tego punktu i nie należy go mylić z wartością najmniejszą i największą funkcji!
Pojęcia wartość największa lub wartość najmniejsza są globalne, a więc odnoszące się do całego zbioru, w którym określona jest dana funkcja.
Funkcja f może mieć w przedziale określoności kilka minimów i maksimów lokalnych, ale tylko jedną wartość najmniejszą i największą, która nie koniecznie musi być ekstremum lokalnym.
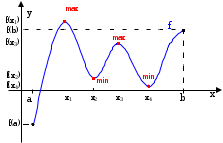
Na przedstawionym rysunku funkcja f w punktach x1 i x3 ma maksimum lokalne, a w punktach x2 i x4 minimum lokalne. Jednocześnie zauważmy, że najmniejszą wartością tej funkcji w przedziale [a, b] jest f(a), a największą f(x1). Tak więc w przedziale [a, b] funkcja f osiąga w punkcie x=a minimum globalne (mimo, że nie jest to minimum lokalne!), a w punkcie x=x1 maksimum globalne.
Ponieważ bezpośrednio z definicji trudno jest wyznaczyć ekstremum, sformułujemy teraz twierdzenia podające warunki konieczne i wystarczające istnienia ekstremum lokalnego funkcji f w punkcie x0.
TWIERDZENIE Fermata
Jeżeli funkcja różniczkowalna f ma w punkcie x0 ekstremum, to f ’(x0)=0.
Twierdzenie Fermata orzeka, że warunkiem koniecznym na to, aby funkcja f różniczkowalna w punkcie x0, miała w tym punkcie ekstremum jest zerowanie się pochodnej w tym punkcie.
Zerowanie się pochodnej w pewnym punkcie nie wystarcza jednak do istnienia ekstremum, w tym punkcie czego dowodem jest poniższy przykład.
Przykład 1.
Funkcja g(x)=x3 nie ma ekstremum w punkcie x0=0 (co jest widoczne na poniższym rysunku), ale jak łatwo sprawdzić g’(0)=0.
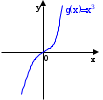
Pojawia się wiec pytanie o warunek wystarczający istnienia ekstremum i określenia jego typu (czy jest to maksimum czy minimum). Odpowiedź jest następująca.
Warunkiem wystarczającym na to, aby funkcja f miała w punkcie x0, w którym pochodna się zeruje (f’(x0)=0) ekstremum jest zmiana znaku pochodnej w tym punkcie, przy czym jeśli pochodna zmienia znak z - na +, to funkcja ma w punkcie x0 minimum, natomiast jeśli pochodna zmienia znak z + na -, to funkcja ma w punkcie x0 maksimum.
Przykład 2.
Zbadajmy ekstrema funkcji f(x)=2x3+3x2-36x+15.
Obliczamy pochodną:
f’(x) = 6x2+6x-36
f’(x) = 6 (x2+x-6),
czyli
f’(x) = 0 wtedy i tylko wtedy gdy x2+x-6 = 0, tj. dla x=-3 i x=2
Badamy teraz znak pochodnej. W tym celu narysujmy jej przybliżony wykres.
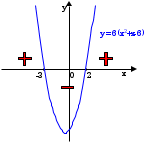
Widzimy więc, że w punkcie x=-3 funkcja ma maksimum (znak pochodnej zmienia się z + na - ) równe fmax(-3)=96, a punkcie x=2 funkcja ma minimum (znak pochodnej zmienia się z - na + ) równe fmin(2)=-19.
Przykład 3.
Zbadajmy jaką najmniejszą i jaką największą wartość przyjmuje funkcja
y = x3-3x2-9x+7 w przedziale [-2,1].
Wyznaczmy najpierw ekstrema lokalne tej funkcji. w tym celu policzmy pochodną
f’(x) = 3x2-6x-9
f’(x) =0 ⇔ 3(x+1)(x-3) = 0 ⇔ x=-1 lub x=3
Liczba 3 nas nie interesuje, gdyż leży poza przedziałem [-2,1]. Natomiast w punkcie x=-1 pochodna zmienia znak z + na -, czyli mamy maksimum lokalne równe fmax(-1)=12.
Aby wyznaczyć ekstremum globalne (wartość największą i najmniejszą) obliczamy ponadto wartośc funkcji w punktach –2 i 1.
f(-2)=5
f(1)=-4
Wartością największą funkcji f w przedziale [-2,1] jest największa spośród liczb: 12,5,-4, czyli 12. Natomiast wartością najmniejszą funkcji f w przedziale [-2,1] jest najmniejsza spośród tych liczb, czyli –4.
IV. Wklęsłość i wypukłość wykresu funkcji.
Wykres funkcji różniczkowalnej w punkcie x0 nazywamy wypukłym (wklęsłym) w tym punkcie, jeżeli istnieje takie otoczenie punktu x0, że dla każdego punktu x z tego otoczenia (oprócz niego samego) punkty P(x, f(x)) wykresu leżą powyżej (poniżej) stycznej poprowadzonej do wykresu w punkcie o odciętej x0.
Wykres funkcji wypukły (wklęsły) w każdym punkcie przedziału (a, b) nazywamy wypukłym (wklęsłym) w tym przedziale.
Przykładem funkcji, która ma wykres wypukły jest funkcja f , natomiast o wykresie wklęsłym funkcja g.
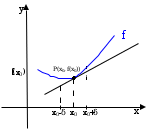 y”>0
y”>0 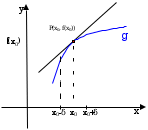 y”<0
y”<0
Jeżeli w pewnym punkcie x0 wykres funkcji f zmienia się z wypukłego na wklęsły lub odwrotnie, to punkt P(x0, f(x0)) nazywamy punktem przegięcia krzywej y=f(x).
Okazuje się, że przy pomocy pochodnych można w łatwy sposób badać wypukłość krzywych oraz wyznaczać ich punkty przegięcia. Zachodzą mianowicie następujące twierdzenia:
TWIEWDZENIE 1. Jeżeli druga pochodna funkcji f jest dodatnia w każdym punkcie przedziału (a, b), to wykres funkcji f jest w tym przedziale wypukły.
TWIERDZENIE 2. Jeżeli druga pochodna funkcji f jest ujemna w każdym punkcie przedziału (a, b), to wykres funkcji f jest w tym przedziale wklęsły.
TWIERDZENIE 3. Jeżeli druga pochodna funkcji f spełnia warunki:
f’’(x0)=0
w otoczeniu punktu x0 ma po obu stronach tego punktu różne znaki,
to punkt P(x0, f(x0)) jest punktem przegięcia wykresu funkcji f.
Przykład.
Zbadamy wypukłość i wyznaczymy punkty przegięcia wykresu funkcji f(x) = 2x3+3x2-4x+10.
Policzmy pochodne (pierwszą i drugą):
f’(x) = 6x2+6x-4 f’’(x) = 12x+6 = 6 (2x+1)
i narysujmy przybliżony wykres pochodnej
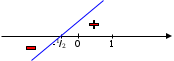
Widzimy zatem, że wykres funkcji f jest wypukły w przedziale (-1/2, +∞) (druga pochodna funkcji f jest dodatnia), natomiast w przedziale (-∞,-1/2) wklęsły (druga pochodna funkcji f jest ujemna).
Ponieważ w punkcie x0=-1/2 druga pochodna zeruje się i zmienia w otoczeniu tego punkty znak, to punkt x0=-1/2 jest punktem przegięcia wykresy tej funkcji.
Wzory na pochodne
Pochodne funkcji elementarnych:
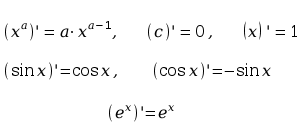
Wzory ogólne: Jeżeli funkcje f(x) i g(x) są różniczkowalne, to
[f(x) + g(x)]’ = [f(x)]’ + [g(x)]’
[f(x) - g(x)]’ = [f(x)]’ - [g(x)] ’
[f(x)g(x)]’ = [f(x)]’g(x) + f(x)[g(x)]’
[cg(x)]’ = c[g(x)]’
![]() .
.
Twierdzenia:
(pochodna funkcji odwrotnej) - jeżeli funkcja x=g(y) jest różnowartościowa i ma pochodną [g(y)]’ ≠ 0, to funkcja y=f(x), odwrotna do niej ma pochodną
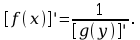
2) (pochodna funkcji złożonej) – jeżeli funkcje u=f(x) i y=g(u) mają pochodne [f(x)]’ oraz [g(u)]’ to funkcja F(x) = g(f(x)) ma pochodną [F(x)]’ = [g(u)]’[f(x)]’.
Pochodne funkcji c.d.:
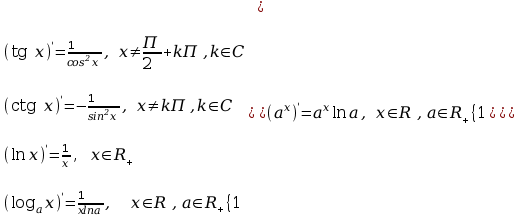
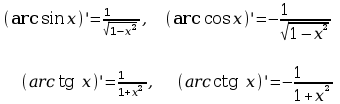
Wyszukiwarka
Podobne podstrony:
wzory poch
Ubytki,niepr,poch poł(16 01 2008)
POCH SA
matematyka podstawowe wzory i Nieznany
Fizyka 2 zadania, wzory
Fizyka Wzory I Prawa Z Objaśnieniami cz 1 [Jezierski, Kołodka]
9a Napiecia dotykowe wzory ozna Nieznany (2)
wniosek o wydanie odpisu aktu urodzenia, Wzory dokumentow
UMOWA PRZECHOWANIA, WZORY UMÓW-SKARBÓWKA,SĄD-ugody,skargi,zlecenia i inne
zalacznik 2, Wzory umów,próśb,pism,pitów,druków
Wzór rezygnacji z usługi NEOSTRADA z TELEWIZJĄ w T.P, Wzory
umowa agencyjna wzor, Dokumenty, różne pisma, Wzory pism
pozew o zachowek, WZORY UMÓW
wzory figur płaskich
UMOWA SPRZEDAŻY NA RATY, WZORY UMÓW-SKARBÓWKA,SĄD-ugody,skargi,zlecenia i inne
99, Prawo, WZORY PISM, Wzory Pism 2