OPRACOWAŁA KATARZYNA WIERCIGROCH

☺

☺

☺

☺

1. Elektron o energii 7.7·10-6J wpada w jednorodne pole magnetyczne o indukcji B= 1.3·10-9 T prostopadle
do linii pola i porusza się po okręgu. Oblicz przyspieszenie całkowite tego ruchu w [m/s2] (me = 9.11·10-31
kg).

9.39e14

R

mV

B

qV

p

p

2

=

2

2

mV

E

=

sin90

o

=1

a

R

V

=

2

2. Elektron przyspieszany w polu elektrycznym o napięciu U=35 V wpada w jednorodne pole magnetyczne
o natężeniu H=8 A/m prostopadle do linii pola i porusza się po okręgu . Oblicz promień tego ruchu w
centymetrach (me = 9.11· 10-31 kg, µo = 4π·10-7 N/A2).

199

R

mV

B

qV

p

p

2

=

=>

qB

mV

R

p

=

sin90

o

=1

2

2

mV

qU

=

3. Elektron przyspieszany w polu elektrycznym o natężeniu E=7.5 V/cm na dystansie x=3.8 cm wpada w
jednorodne pole magnetyczne o natężeniu H=8.3 A/m po kątem α=64o do linii pola i porusza się po spirali.
Oblicz skok tej spirali w milimetrach (me =9.11·10-31 kg)

4760

d

E

U

⋅

=

H

B

⋅

=

µ

qU

mV

=

2

2

R

mV

B

qV

p

p

2

=

p

V

R

T

⋅

=

π

2

T

V

h

r

⋅

=

4. Elektron przyspieszany w polu elektrycznym o napięciu U=11 V wpada w jednorodne pole magnetyczne
o natężeniu H=12 A/m prostopadle do linii pola i porusza się po okręgu . Oblicz promień tego ruchu w
centymetrach (me = 9.11· 10-31 kg, µo = 4π·10-7 N/A2). 74,2197

2

2

mV

qU

=

B

q

mV

R

p

⋅

=

5. Elektron przyspieszany w polu elektrycznym o natężeniu E=6.8 V/cm na dystansie x=9.3 cm wpada w
jednorodne pole magnetyczne o natężeniu H=9.5 A/m pod kątem α=49o do linii pola i porusza się po
spirali. Oblicz okres tego ruchu T w nanosekundach( 10^-9) (me =9.11·10-31 kg)

2,9967e3

q

H

m

T

⋅

⋅

⋅

=

µ

π

2

wyprowadzenie wzoru z zad 3

6. Elektron wpada w jednorodne pole magnetyczne o natężeniu H=7.4 A/m pod kątem α=50 do linii pola i
porusza się po spirali. Oblicz prędkość początkową elektronu v [km/s] jeżeli promień tej spirali jest równy
r=1.7cm (me =9.11·10-31 kg)

α

sin

V

V

p

=

R

mV

B

qV

p

p

2

=

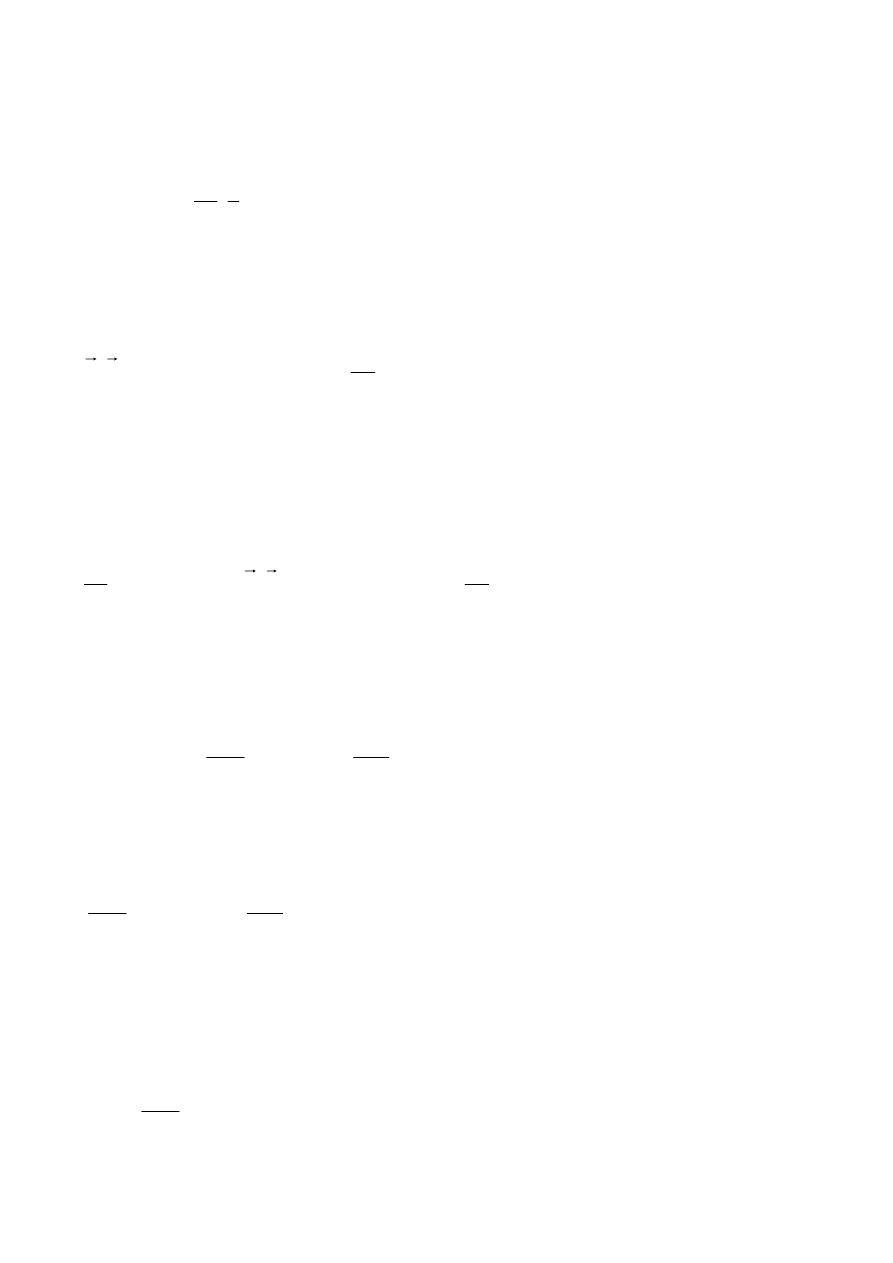
1

7. W dwóch, równoległych, długich przewodnikach płyną prądy I1 i I2 w tym samym kierunku. Jaka musi
być różnica natężeń prądów I1-I2 [mA] jeżeli odległość między przewodnikami wynosi d = 8.8cm a
indukcja pola magnetycznego B w połowie odległości między nimi wynosi 3.4·10-5 T.

7480

x=0.5d

x

I

B

⋅

=

π

µ

2

8. Z drutu miedzianego o długości l=100 cm utworzono ramkę w kształcie kwadratu i umieszczono w polu
magnetycznym o indukcji B=7.1·10-4 T prostopadle do linii sił pola. Następnie ramkę obrócono o kąt
α

=15o w czasie t=1.9·10-3s. Jaka będzie wartość siły elektromotorycznej indukcji SEM [mV] powstałej w

ramce ?

0.0794

α

φ

cos

BS

S

B

=

⋅

=

t

∆

∆

=

φ

ε

UWAGA: liczymy dla 90 i odejmujemy policzony dla naszego kąta

9. Z drutu miedzianego o długości l=31 cm utworzono ramkę w kształcie okręgu i umieszczono w polu
magnetycznym o indukcji B=8.4·10-4 T prostopadle do linii sił pola. Następnie ramkę obrócono o kąt
α

=90o w czasie t [ms] W jakim czasie wykonano ten obrót jeżeli wartość siły elektromotorycznej indukcji

SEM powstałej w ramce wynosiła 9.9 mV?

π

2

l

r

=

BS

S

B

=

⋅

=

φ

ε

φ

∆

=

∆

t

10. Elektron przyspieszany w polu elektrycznym o natężeniu E=2.7 V/cm na dystansie x=3 cm wpada w
jednorodne pole magnetyczne o indukcji B=8.3·10-9 T prostopadle do linii pola i porusza się po okręgu.
Oblicz prędkość kątowa tego ruchu ω [rad/s] (me =9.11·10-31 kg)

1,4777e3

R

V

⋅

=

ω

2

2

mV

qU

=

B

q

mV

R

p

⋅

=

11. Elektron o energii 6.1·10-19J wpada w jednorodne pole magnetyczne o natężeniu H= 3.3 A/m
prostopadle do linii pola i porusza się po okręgu . Oblicz promień tego ruchu w metrach.

1,58889

2

2

mV

E

=

qB

mV

R

p

=

12. Elektron o energii 7.7 eV wpada w jednorodne pole magnetyczne o indukcji B= 3.7·10-5 T pod kątem
α

=16o do linii pola i porusza się po spirali. Oblicz prędkość całkowitą tego ruchu w [km/s] po czasie

t=3.3·10-3s (me =9.11·10-31 kg).

2

2

mV

E

=

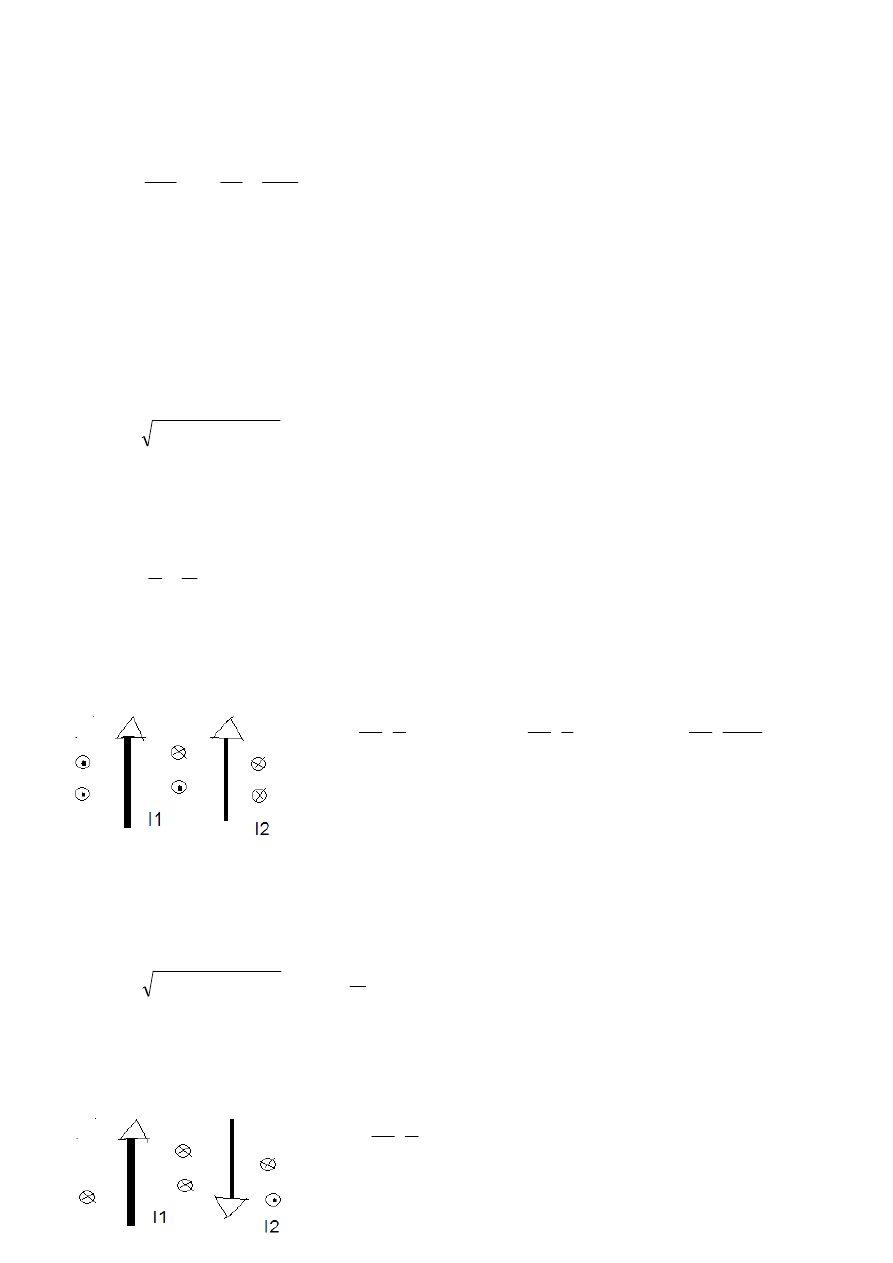
2

13. Dwa kołowe, współśrodkowe przewodniki o promieniach r1=0.2m i r2=0.6m leżą w jednej
płaszczyźnie. W przewodnikach, w tym samym kierunku, płyną prądy, odpowiednio I1=7.6A i I2=7.5A. Ile
wynosi stosunek indukcji pola magnetycznego B1/B2, w środku układu przewodników?

3,039

R

I

H

π

2

=

2

1

2

1

H

H

B

B

µ

µ

=

14. Prosty przewodnik miedziany, w którym płynie prąd o natężeniu I = 1.1 A umieszczono w jednorodnym
polu magnetycznym o indukcji B = 5 T, prostopadle do linii sił pola. Jaka jest długość tego przewodnika L
[cm], jeżeli siła F z jaką pole magnetyczne działa na przewodnik wynosi 2.9 N.

52,72

l

BI

F

∆

=

15. Kondensator o pojemności 10 µF oraz opór omowy 148 Ω są włączone szeregowo do sieci prądu
zmiennego o napięciu 220 V i częstotliwości 468 Hz. Obliczyć zawadę tego obwodu.

151,86

2

2

)

(

C

L

X

X

R

Z

−

+

=

16. Na jeziorze wzbudzono falę, która dobiegła do stromego brzegu po upływie t = 8 min. Odległość między
grzbietami fali wynosi l = 1 m, a czas między kolejnymi uderzeniami grzbietów o brzeg to = 10 s. W jakiej
odleglości s (w metrach) od brzegu wzbudzono falę?

48

0

t

l

T

V

f

=

=

D

t

V

s

f

=

17. W dwóch, równoległych, długich przewodnikach płyną prądy I1=3.1A i I2=7.7A w tym samym
kierunku. W jakiej odległości x [m] od przewodnika pierwszego, w przestrzeni między nimi, indukcja pola
magnetycznego będzie równa zeru. Odległość między przewodnikami wynosi d=1.5m.

0,431

d

I

B

⋅

=

π

µ

2

x

I

H

⋅

=

π

2

1

1

x

d

I

H

−

⋅

=

π

2

1

2

H

1

=H

2

18. Do sieci miejskiej prądu zmiennego o napięciu maksymalnym 255 V włączono szeregowo przewodnik o
oporze czynnym 144 mΩ i cewkę o indukcyjności 21.7 mH. Znaleźć częstotliwość f prądu, jeżeli amplituda
natężenia prądu w obwodzie jest równa 4.99 A.

2

2

)

(

C

L

X

X

R

Z

−

+

=

Z

U

I

=

19. W dwóch, równoległych, długich przewodnikach płyną prądy I1=2.2A i I2=9.5A w przeciwnych
kierunkach. Ile wynosi natężenie pola magnetycznego H [A/m] w odległości x=0.4m od przewodnika
drugiego, w przestrzeni między nimi. Odległość między przewodnikami wynosi d=1.6m.

d

I

B

⋅

=

π

µ

2

H= H

1

+ H

2

3

20. W pewnym obwodzie prądu przemiennego opór indukcyjny wynosi 73 i jest równy oporowi omowemu,
a opór pojemnościowy nie występuje. Wyznacz przesunięcie fazowe natężenia prądu względem napięcia w
tym obwodzie.

2

2

)

(

C

L

X

X

R

Z

−

+

=

Z

R

=

α

cos

21. Kolejarz uderza młotem w szynę. Znajdujący się w odległości l Krzysiu rejestruje dźwięk biegnący
przez szynę i powietrze w chwilach różniących się o Dt = 0.8 s. Szybkość rozchodzenia się dźwięku w
powietrzu v1 = 330 m/s, w stali v2 = 5300 m/s. Oblicz odległość l ( w metrach).

t

V

s

s

=

)

(

t

t

V

s

p

∆

+

=

22. Znaleźć wychylenie x (w cm) punktu z położenia równowagi w chwili t = T/8, jeżeli punkt ten znajduje
się w odległości z = D/12 (D - długość fali) od źródła drgań o amplitudzie A = 7.2 cm.

-1,86

t

π

ω

2

=

)

sin(

ϕ

ω

+

−

=

t

kx

A

X

pr

D

π

2

=

k

23. Prosty drut miedziany o długości l=2.5 cm przemieszcza się ruchem jednostajnym w polu
magnetycznym o indukcji B=1.4 mT,z prędkością v=3.2 m/s, prostopadle do linii sił pola. Jak będzie
wartość siły elektromotorycznej indukcji powstałej w tym drucie [mV]?

B

l

V

F

⋅

⋅

=

24. Elektron o energii 2.4 eV wpada w jednorodne pole magnetyczne o indukcji B= 7.5·10-5 T pod kątem
α

=48o do linii pola i porusza się po spirali. Oblicz prędkość całkowitą tego ruchu w [km/s] po czasie

t=9.3·10-3s (me =9.11·10-31 kg).

2

2

mV

E

=

25. Jaka jest pojemność kondensatora włączonego do obwodu prądu przemiennego, którego opór
pojemnościowy ma wartość 144 przy częstotliwości prądu 68 s-1? (Wynik podać w F.)

fC

L

X

c

π

ω

2

1

1

=

=

26. Prosty drut miedziany o średnicy d=7.5 mm i długości l=8.7 cm przemieszcza się ruchem jednostajnym
w polu magnetycznym o indukcji B, z prędkością v =1.7 m/s, prostopadle do linii sił pola. Jaka musi być
indukcja pola magnetycznego B [mT] aby moc wyindukowanego w drucie prądu wynosiła P= 6.1 mW.
Opór właściwy miedzi 1.7·10-8 Ωm ?

3,06

S

l

R

ρ

=

R

l

V

B

P

2

2

2

=

4

2

d

S

π

=

27. Dwa kołowe, współśrodkowe przewodniki o promieniach r1=0.5m i r2 =7.9m leżą w jednej
płaszczyźnie. W przewodnikach, w przeciwnym kierunku, płyną prądy, odpowiednio I1=2A i I2=7.3A. Jaka
jest wartość indukcji pola magnetycznego B w środku układu przewodników w [µ T]? (µo = 4π·10-7 N/A2)

r

I

B

⋅

=

2

µ

B= B

1

- B

2

4

28. Drgania kamertonu nastrojonego na częstość f = 494 Hz wywołują falę stojącą w strunie
unieruchomionej na obu końcach. Prędkość rozchodzenia się fali w strunie wynosi V = 328 m/s. Na strunie
powstały n = 8 strzałek o amplitudzie A = 5 mm. Oblicz maksymalną prędkość poprzeczną V1 (w m/s)
struny.

f

π

ω

2

=

ω

A

V

=

29. Znaleźć indukcyjność cewki w obwodzie prądu zmiennego, jeżeli amplituda napięcia na jej końcach
wynosi 149 V, amplituda natężenia prądu jest równa 2.7 A, a częstotliwość prądu wynosi 148 Hz. Pominąć
opór czynny cewki. Wynik podać w [H]

2

c

X

Z

=

Z

U

I

=

30. Znaleźć różnicę faz (w radianach) między dwoma punktami fali dźwiękowej rozchodzącej się w
powietrzu, jeżeli są one odległe od siebie o l = 0.6 m, a częstotliwość drgań fali wynosi f = 409 Hz.
Prędkość dźwięku v = 340 m/s

f

V

T

V

f

f

=

=

D

kl

x

x

k

=

−

=

)

(

2

1

ϕ

31. Na wysokości h=679m nad miejscem wystrzelenia jednocześnie usłyszano huk wystrzału i zauważono
kule. Jaka była Vo kuli? Prędkość dźwięku V=340m/s a g=9.81m/s^2

t

H

V

d

=

2

2

at

t

V

H

k

−

=

32. Znaleźć częstotliwość tomu podstawowego struny o napięciu siły F=5853N. Dł struny l=1.1m, a jej
ciężar Q=0.02N

ρ

S

F

S

E

V

=

=

D

V

f

=

2

D

=

l

S

V

l

=

ρ

ρ

V

Q

v

m

=

=