Magnusson r.6 - „Standardowy błąd pomiaru”
zad. 1 (str.132)
Oblicz błąd standardowy pomiaru dla testów o następujących odchyleniach standardowych i współczynnikach rzetelności:
test |
odchylenie stand. - st |
rzetelność rtt |
a |
10 |
0,90 |
b |
15 |
0,95 |
c |
2 |
0,85 |
zad. 2 (str.132)
Pewna osoba uzyskała w trzech testach z ćw.1 następujące wyniki surowe a) 55 b) 60 c) 6. Między jakimi wynikami surowymi z prawdopodobieństwem 95-procentowych leżą wyniki prawdziwe tej osoby w trzech mierzonych zmiennych?
zad. 7 (str.133)
W teście o odchyl. stand. 15 i rzetelności 0,875, osoba uzyskała wynik surowy 90. W jakich granicach leży z 95-procentową pewnością wynik prawdziwy tej osoby?
→ tj - wyniki surowe
→ se = st ![]()
→ Z![]()
= rozkład.normalny.s.odw(![]()
)
→ Tl = tj - se ⋅ z![]()
→ Tu = tj + se ⋅ z![]()
→ < → zaokr.do.całk.( Tl)
→ > → zaokr.do.całk.( Tu)
zad. 3 - 6 (str.132-133)
zad |
os. |
odchylenie stand. - st |
rzetelność rtt |
wynik prawdziwy Tj |
wynik surowy tj |
3 |
|
12,5 |
0,84 |
130 |
146 |
4 |
a |
12,5 |
0,84 |
119 |
124 |
|
b |
12,5 |
0,84 |
115 |
124 |
|
c |
12,5 |
0,84 |
110 |
124 |
5 |
a |
10 |
0,84 |
50 |
46 |
|
b |
10 |
0,84 |
50 |
42 |
|
c |
10 |
0,84 |
50 |
38 |
6 |
a |
15 |
0,875 |
100 |
90 |
|
b |
15 |
0,875 |
80 |
90 |
→ se = st ![]()
→ Z![]()
= modul.liczby(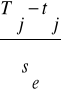
)
→ P = rozkład.normalny.s (Z![]()
)
→ p = 1 - P /gdy nie ma kierunku różnicy p · 2
Wyszukiwarka
Podobne podstrony:
Zadania do zestawu 4 - rozdzial 7, Psychometria, zadania i wzory
Zadania do zestawu 5 - rozdział 9, Psychometria, zadania i wzory
Zadania do zestawu 4 - rozdzial 7, Psychometria, zadania i wzory
~$dania do zestawu 5 rozdział 9
Zadania do zestawu 3B i 3C - rozdzial 6, Psychometria, zadania i wzory
Zadania do zestawu 3A - rozdzial 6, Psychometria, zadania i wzory
Zadania do zestawu 7 - test - Magnusson r 12, Psychometria, zadania i wzory
Zadania do zestawu 6 - Brzezinski r 15, Psychometria, zadania i wzory
Rohleder, Fizyka II Ć, zadania i wzory do rozwiązania
Zadania - r5, Psychometria, zadania i wzory
zadania do kolokwium2 odpowiedzi, psychologia, statystyka
18. Zadania do procesu wychowania, Psychologia, Teoretyczne podstawy wychowania
Fizyka 2 zadania, wzory
zadanie wzory
Rozdział 7 - Rozwój fizyczny i poznawczy w wieku od dwóch do sześciu lat, Psychologia rozwojowa, Hel
BILANS, BILANS CIEPLY, Bilans cieplny silnika jest to zestawienie rozdziału ciepła dostarczonego do
Zadania wzory empiryczne
więcej podobnych podstron