39. Rachunek zdań. Spójniki zdaniowe, funkcje zdaniowe. Tautologie.

Rachunek zdań (ang. propositional calculus)

to dział logiki matematycznej badający związki między zdaniami (zmiennymi zdaniowymi -zmienna zdaniowa to zmienna występująca w rachunku zdań, mogąca przybierać wartości prawda lub fałsz.) lub funkcjami zdaniowymi utworzonymi za pomocą spójników zdaniowych ze zdań lub funkcji zdaniowych prostszych. Rachunek zdań określa sposoby stosowania spójników zdaniowych w poprawnym wnioskowaniu.

W klasycznym rachunku zdań przyjmuje się założenie, że każdemu zdaniu można przypisać jedną z dwu wartości logicznych - prawdę lub fałsz, które umownie przyjęto oznaczać 1 i 0; dlatego klasyczny rachunek zdań nazywa się dwuwartościowym rachunkiem zdań.

W rachunku zdań treść rozpatrywanych zdań nie ma znaczenia, ważna jest jedynie ich wartość logiczna. Wartość logiczną zdań złożonych powstałych przez zastosowanie spójników zdaniowych określa funkcja prawdziwościowa, związana z każdym spójnikiem zdaniowym. Wartość ta zależy wyłącznie od prawdziwości lub fałszywości zdań składowych, nie zależy natomiast od ich treści.

Szczególną rolę w rachunku zdań odgrywają takie zdania złożone, których wartość logiczna jest równa 1, niezależnie od tego, jakie wartości logiczne mają zdania proste, z których są one zbudowane. Takie zdania nazywa się prawami rachunku zdań lub tautologiami.

Funkcja zdaniowa to wyrażenie zawierające zmienne wolne, które w wyniku związania tych zmiennych kwantyfikatorami lub podstawienia za nie odpowiednich nazw staje się zdaniem.

Dla funkcji (formy) zdaniowej F(x) o jednej zmiennej wolnej x, rozważanej w zbiorze X, wprowadza się pojęcie dziedziny DX(F) funkcji zdaniowej, obejmując tą nazwą podzbiór elementów zbioru X o tej własności, że po podstawieniu w formie zdaniowej F(x) w miejsce zmiennej x nazw tych elementów otrzymuje się zdanie prawdziwe lub fałszywe.

Każde równanie i każda nierówność z jedną niewiadomą jest funkcją (formą) zdaniową, której dziedziną jest pewien zbiór liczb. Każde równanie z dwiema lub więcej niewiadomymi jest funkcją (formą) zdaniową, której dziedziną jest zbiór par lub trójek lub odpowiedno większej ilości liczb.

Jeżeli zdanie F(a) jest prawdziwe, to mówi się, że element a spełnia formę zdaniową F(x). Zbiór elementów zbioru X spełniających daną formę zdaniową nazywa się wykresem formy zdaniowej w X.

Przykład

Forma zdaniowa x>2 zamienia się w zdanie dla tych x, dla których ten zapis ma sens. Wszelkie liczby rzeczywiste należą więc do jej dziedziny, podczas gdy na przykład nazwa SŁOŃ lub liczba zespolona 1+2i już nie.

Kwantyfikatory

1.
kwantyfikator duży; ogólny.

Dla każdego x∈X zachodzi (spełniona jest własność)
. Zdanie to, wyrażone kwantyfikatorem ogólnym jest zdaniem prawdziwym, wtedy i tylko wtedy, gdy dla dowolnego, ustalonego x∈X zdanie
jest prawdziwe, co oznacza, że:

2.
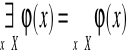
kwantyfikator szczegółowy; mały; egzystencjalny.

Istnieje takie x∈X, że zachodzi
. Zdanie wyrażone kwantyfikatorem szczegółowym, jest zdaniem prawdziwym, wtedy i tylko wtedy, gdy dla pewnego x∈X zdanie
jest prawdziwe, co oznacza, że:
.

Tautologia

to definicja, twierdzenie lub zdanie warunkowe, w którym występuje zapętlenie poprzez odniesienie do samego siebie.

Przykłady

· Prawda to to, co się naprawdę wydarzyło. (tautologiczna definicja)

· Jeśli to zdanie jest prawdziwe, to jest ono prawdziwe. (tautologiczne twierdzenie)

Nie wszystkie przypadki tautologii są takie oczywiste, na przykład zdanie „Fakt to zdarzenie, które się naprawdę wydarzyło” jest tautologią, ponieważ prawda to stwierdzenie, które ma potwierdzenie w faktach.

W logice tautologia to takie zdanie, które jest zawsze prawdziwe niezależnie od wartości logicznej składników tego zdania.

Natomiast w gramatyce tautologie są czasem stosowane dla podkreślenia czegoś, a pozorne tautologie, żeby użyć dwóch znaczeń tego samego słowa (na przykład "duże duże litery" oznacza kapitaliki dużych rozmiarów). Często jednak są po prostu błędem stylistycznym i należy starać się ich unikać.

Spójniki

Zdania proste można łączyć funktorami zdaniotwórczymi:
(lub),
(i),
(jeżeli...to...),
(wtedy i tylko wtedy gdy),  (nieprawda, że...), tworząc w ten sposób zdanie złożone.

Zdania proste zapisujemy: p, q, r, s,

1. zdanie ~ p (nieprawda, że p) nazywamy zaprzeczeniem (negacją zdania).

Negacja zmienia wartość logiczną zdania na przeciwną

Zdanie: Dzisiaj jest wtorek (prawda) i jego negacja: Nieprawda, że dzisiaj jest wtorek (fałsz).

p	~p
1	0
0	1

2. zdanie p
   q (p i q) nazywamy koniunkcją zdań p i q. Koniunkcja zdań jest prawdziwa, gdy oba zdania są prawdziwe. W przeciwnym wypadku jest fałszywa.

Koniunkcją zdań: Warszawa jest stolicą Polski (prawda). Warszawa leży nad Wisłą (prawda), jest zdanie: Warszawa jest stolicą Polski i leży nad Wisłą.

p	q	p ^ q
1	1	1
1	0	0
0	1	0
0	0	0

3. Zdanie p
   q (p lub q) nazywamy alternatywą zdań p i q. Alternatywa dwóch zdań jest prawdziwa, gdy co najmniej jedno ze zdań jest prawdziwe, a fałszywa, gdy obydwa zdania są fałszywe.

Alternatywą zdań: Zakopane leży w górach (prawda). Zakopane leży nad morzem (fałsz) jest zdanie: Zakopane leży w górach lub nad morzem (prawda).

p	q	p v q
1	1	1
1	0	1
0	1	1
0	0	0

4. Zdanie p
   q (jeżeli p to q) nazywamy implikacją zdań p i q. Zdanie p nazywamy poprzednikiem implikacji, zdanie q jej następnikiem. Implikacja jest fałszywa tylko wtedy, gdy poprzednik jest prawdziwy a następnik fałszywy.

Implikacją zdań: Dzisiaj jest niedziela (fałsz). Nie idę do szkoły (prawda), jest zdanie: Jeżeli dzisiaj jest niedziela to nie idę do szkoły (prawda).

p	q	p => q
1	1	1
1	0	0
0	1	1
0	0	1

5. Zdanie p
   q (p wtedy i tylko wtedy gdy q) nazywamy równoważnością zdań p i q. Równowartość jest prawdziwa gdy zdania p i q są obydwa prawdziwe, albo obydwa fałszywe.

p	q	p q
1	1	1
1	0	0
0	1	0
0	0	1

Prawo zaprzeczenia implikacji:




---