Ćwiczenie 2.

Discrete Fourier Transform (DFT).

Dyskretna Transformata Fouriera. Metody obliczania i podstawowe właściwości.

ZADANIA

Zadanie 1

Oblicz DFT ciągu {x_n}=……………………………………………….

Stosując wzór definicyjny (napisz m-skrypt lub m-funkcję, pamiętaj o unikatowej nazwie, np. moja_dft1….)

Narysuj widmo amplitudowo-fazowe transformaty {X_n}.

Porównaj otrzymane wyniki z tymi uzyskanymi z pomocą wbudowanej funkcji fft.

Zadamie 2

Sformułuj i zweryfikuj numerycznie (zilustruj odpowiednimi m-procedurami) następujące właściwości transformaty DFT:

1. Okresowość

2. Liniowość

3. Symmetris

Uwaga: Symmetria: Jeżeli X_k jest transoramatą DFT ciągu x[n], wówczas

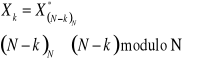
Pytanie dodatkowe : Jaka jest symetria
oraz
jeżeli N jest liczbą parzystą.?

Zadanie 3

Porównaj czas wykonywania procedury fft z napisaną własnoręcznie (Zadanie 1). Zastosuj parę komend ti, toc ( toc mierzy czas od momentu wykonania tic). Stwórz m-plik do pomiarów testowych, skomentuj otrzymane wyniki.

Uwagi:

1. porównaj DFT oraz FFT dla N=110 , N=2048, N=4096

utwórz wektor n=0:N-1; x=(-1)^n

2. przykładowy kod procedury testowej:

1. N=500;

2. n=0:N-1;

3. x=(-1).^n;

4. disp('my DFT');

5. tic

6. X=mydft(x);

7. toc

8. disp('FFT');

9. tic

10. X=fft(x);

11. toc

Zadanie 4

Zaimplementuj nowy test porównawczy dla procedury fft: porównaj szybkość fft dla: N=2^20, N=950000, N=750000, N=550000. Skomentuj wyniki!

UWAGA: zastosuj dyskretny wektor o wartościach x=(-1)^n.

Zadanie 5

Napisz m-skrypt (lub m-funkcję) obliczjącą odwrotną dyskretną transformatę Fouriera (ze wzoru definicyjnego! - porównaj jej działanie z wbudowaną funkcją ifft.

Zadanie 6

Oblicz dyskretny splot sygnałów okresowych (N=4):

x₁(n)=…………………………

x₂(n)=…………………………

Zastosuj:

1. Procedurę z poprzedniego ćwiczenia.

2. Procedurę wbudowaną conv

3. Twierdzenie o DFT splotu ciągów okresowych .

Zadanie 7

Powtórz poprzednie zadanie dla ciągów nieokresowych x₁(n) i x₂(n),

W jakich warunkach można i czy w ogóle stosować tu Twierdzenie o DFT splotu kołowego (sygnałów okresowych)?

Materiały pomocnicze:

1. Procedury służące do obliczania Dyskretnej Transformaty Fouriera i Odwrotnej Dyskretnej Transformaty Fouriera (Matlab 5.3):

Syntax (Składnia)

Y = fft(X)

Oblicza i umieszcza w wektorze Y Dyskretną Transformatę Fouriera obliczoną algorytmem FFT.

Y = fft(X,n)

Oblicza i umieszcza w wektorze Y n-punktową FFT (jeśli długość X jest mniejsza niż n, wektor X jest uzupełniany zerami, jeśli długość X jest większa to wektor jest skracany)

Y = fft(X,[],dim)

Y = fft(X,n,dim)

Wykonuje FFT „wzdłuż” wymiaru dim macierzy X.

.

.

Funkcje X = fft(x) oraz x = ifft(X)stanowią parę dysktretych transformat Fouriera (prosta i odwrotna) dla wektorów o długości N:

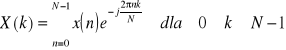
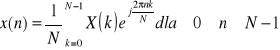
2. Procedury potrzebne do operacji na liczbach zespolonych:

1. complex c = complex(a,b) tworzy zespoloną liczbę (w zasadzie wektor) z dwóch liczb (wektorów) rzeczywistych i jest niezwykle użytecznym odpowiednikiem innego zapisu liczby zespolonej:

2. imag zwraca część urojoną liczby zespolonej

3. real zwraca część rzeczywistą liczby zespolonej

4. abs umożliwia wyznaczenie modułu liczby zespolonej

5. angle zwraca argument liczby zespolonej

6. conj wyznacza wartość sprzężoną liczby zespolonej.

3. Definicja splotu dyskretnego:

4. Definicja splotu funkcji dyskretnych okresowych (o okresie N):

W przypadku splotu funkcji okresowych można wykorzystać Twierdzenie o transformacie splotu dyskretnego: Jeżeli X₁(n) i X₂(n) są transformatami DFT okresowych ciągów x₁(n) oraz x₂(n), wówczas:

gdzie IDFT oznacza odwrotną transformatę dyskretną Fouriera.

1

---