1. Naszkicuj wykres funkcji

1. f(x) = -x

2. f(x) = -2x+2

3. f(x) = 2x+1 gdzie
   

4. 
   

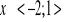
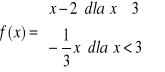
2. Znajdź wzór funkcji liniowej f wiedząc, że:

1. f(-1)=2 i f(3)=-2

2. jej wykres przecina oś OY w punkcie o rzędnej 4, a 2 jest miejscem zerowym funkcji f

3. jej wykres przechodzi przez punkty A=(1,2) i B=(5,6)

4. jej wykres przechodzi przez punkt C=(4,3) i jest równoległy do wykresu funkcji g(x)= 3x+7

5. f nie przyjmuje wartości dodatnich i f(22)=-3

3. Rozwiąż algebraicznie i graficznie układ równań:

1. 
   

2. 
   

3. 
   

4. 
   

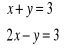
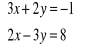
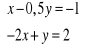
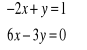
4. Funkcja określona jest wzorem
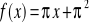
   .Prosta k jest wykresem funkcji f.

1. Wyznacz te argumenty, dla których funkcja f przyjmuje wartości nieujemne.

2. Oblicz współrzędne punktu przecięcia prostej k z wykresem funkcji g(x)=x+
   .

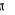
3. Znajdź równanie prostej przechodzącej przez punkt K=(-1;
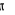
   ) i równoległej do prostej k.

5. Funkcja f określona jest wzorem f(x)=4x+1. O funkcji g wiemy, że:

1. współczynnik kierunkowy prostej, która jest wykresem funkcji g, jest liczbą przeciwną do współczynnika kierunkowego prostej będącej wykresem funkcji f.

2. miejsce zerowe funkcji g jest liczbą odwrotną do miejsca zerowego funkcji f.

Znajdź wzór funkcji g.

6. Znajdź wykres funkcji g(x) prostopadłej do wykresu funkcji f(x), jeżeli:

1. f(x)= 2x+1 i g(x) przechodzi przez punkt A=(4,1)

2. f(x)= 3x-2 i miejsce zerowe funkcji g(x)= 4

3. f(x)=
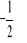
   x-3 i punkt przecięcia funkcji g(x) z osią OX wynosi 5.

4. f(x)=
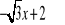
   i funkcja f(x) przecina się z funkcją g(x) w punkcie A=(0,2)

7. Funkcja f jest liniowa. Zbiorem rozwiązań nierówności f(x)>8 jest przedział (-
   ;-1), a zbiorem rozwiązań nierówności f(x)
   -2 jest przedział <-4;+
   ). Znajdź wzór funkcji f.

8. Dzięki jakim przekształceniom z wykresu funkcji f(x)=x powstał wykres funkcji g(x), jeżeli jest on określony wzorem:

1. g(x)= 2x+1

2. g(x)=-x+3

3. g(x)=x-4

4. g(x)=-4x-2

9. Jak należy przesunąć wykres funkcji y=x², aby otrzymać funkcję:

1. g(x)= (x+1)²+3

2. g(x)=-(x-1)²-2

3. g(x)=x²+4

4. g(x)=x²-2x+1

10. Funkcja f określona jest wzorem f(x)= 3x+b

1. wyznacz te wartości współczynnika b, dla których wartość funkcji f przyjmowana dla argumentu 5 jest mniejsza od 2.

2. wyznacz te wartości współczynnika b, dla których miejsce zerowe funkcji f jest większe od 3,5.

---