AISDE - Kolokwium 2 poprawkowe 23 czerwca 2008

Podpis

Zadanie 1 (4p)

Do słownika BST zawierającego klucze {1.0, 3.0, 6.0} wstawiamy klucz rzeczywisty x wy­lo­sowany z rozkładem równomiernym z prze­działu <0, 10>. Operacja wyszukania klucza 1.0 wymaga 1 porównania, klucza 3.0 - 2 po­równań. Obliczyć złożoność oczekiwaną A wyszukania klucza x. Porównanie to operacja comp(v,k) dająca wynik -1, 0, 1.

A = ................

Zadanie 2 (4p)

Słownik zaimplementowany w tablicy upo­rz­ą­d­kowanej zawiera klucze {1,2,...,10}. Nary­sować drzewo podziału binarnego. Jaka jest wysokość drzewa h? Ilu porównań comp(v,k) wymaga wyszukanie klucza 1? Dobrać war­to­wników tak, by wyszukiwanie algoryt­mem search_tu_int każdego istniejącego klucza wymagało 1 porównania.

Drzewo podziału binarnego h=............................................................... Wyszukanie klucza 1 wymaga ....... porównań Wartownicy to:........................................

Zadanie 3 (4p)

Wyszukanie algorytmem Rabina-Karpa przy q=6541 w tekście T o długości n=7 nad V= {0,1} wszystkich wystąpień wzorca P o dłu­gości 4 wymagało t(n)=16 porównań symboli. Określić T i P. Znaleźć wszystkie rozwiązania

Ile rozwiązań istnieje? .................................. T=................................................................... P=................................................................... T=................................................................... P=...................................................................

Zadanie 4 (6p)

Stworzyć automat wyszukujący dwa wzorce P1=[10] i P2=[01] nad alfabetem V={0,1,2}. Ile stanów akceptujących zawiera automat? Z ilu elementów składa się tablica przejść automatu? Ile operacji string_comp wymaga stworzenie tego automatu? Ile porównań symboli wymagałoby wyszu­ka­nie P1 i P2 algorytmem Naive w tekście T=[0101]?

Graf automatu Liczba stanów akceptujących=..................... Liczba elementów tablicy przejść = ............ Liczba operacji string_comp=...................... Liczba porównań w algorytmie Naive=.......

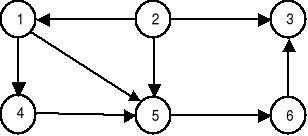
Zadanie 5 (4p)

Podany graf skierowany przeszukujemy algo­ryt­mem BFS z wierzchołka 1. Opisać atrybuty d wierzchołków. Pogrubić drzewo przeszu­ki­wania. Określić najkrótszą ścieżkę p(1,3), wyrazić jej długość za pomocą elementów tablicy d. Określić max(d).

p(1,3)=......................................................... |p(1,3)|=........................................................ max d = .......................................................

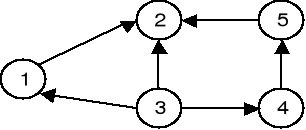
Zadanie 6 (4p)

Dla podanego grafu wykonujemy algorytm DFS z wierzchołka 1 i restartem z kolejnego wierzchołka według numeracji. Opisać graf atrybutami d/f. Pogrubić drzewo przeszuki­wania. Sklasy­fi­kować gałęzie. Czy graf jest cykliczny? Ile zawiera składowych silnie spójnych SCC? Posortować topologicznie wierz­chołki V. Jaka jest reguła sortowania topologicznego za pomocą DFS?

gałęzie drzewa:............................................... cięciwy powrotne:.......................................... cięciwy w przód:............................................ cięciwy zwykłe:............................................. Czy cykliczny? ............................................. Liczba SCC=................................................. Sortowanie topologiczne V:.......................... Reguła:.......................................................... ...................................................................... ......................................................................

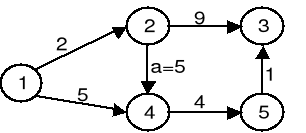
Zadanie 7 (5p)

Podany graf o wagach całkowitych dodatnich przeszukujemy algorytmem Dijkstry z wierz­chołka 1. Opisać graf atry­butami d. Pogrubić drzewo minimalnych ścieżek. Jaka jest złożo­ność algorytmu, jeżeli operacją dominu­jącą jest wywołanie funkcji realizującej relaksacje? Ile razy relaksacja do­­konała zmniejszenia wa­r­­tości d? O ile najmniej trzeba zmniejszyć wagę a, by algorytm poszedł do wierzchołka 3 po kra­wędzi (2,4)? Ile porównań wykona algorytm extractmin?

Złożoność=....................................................... Liczba zmniejszeń d=....................................... Trzeba zmniejszyć a o ..................................... Liczba porównań=............................................

---