Politechnika Rzeszowska

Stanisław Jędrzejewski

II MDM

Gr. Lab.83

Laboratorium z mechaniki płynów

PONIEDZIAŁEK

tydzień A

godz. 14

TEMAT ĆWICZENIA:

Wyznaczanie wykresu piezometrycznego.

CEL ĆWICZENIA:

Zapoznanie się z równaniem Bernoulliego dla przepływów rzeczywistych. Wyznaczanie strat za pomocą tego równania. Zapoznanie się z konstrukcją wykresu strat - wykresu piezometrycznego.

Data złożenia

07.05.2001r.

Data przyjęcia

Ocena

1. Opis ćwiczenia:

Do rurociągu zbudowanego z trzech rur, o narastających średnicach, podłączamy ciśnieniomierze rozmieszczone w znanych odległościach. Regulując prędkość przepływu cieczy przez rurociąg, odczytujemy ciśnienie.

2. Wstęp teoretyczny:

Dla zanalizowania pracy rurociągu, wskazania miejsc, gdzie może wystąpić kawitacja, określenia obciążeń warunkujących wytrzymałość konstrukcji, sporządza się wykres ciśnienia w zależności od współrzędnej liniowej mierzonej wzdłuż osi rurociągu. Na tym wykresie odkłada się zmiany ciśnienia wywołane zmianą osi rurociągu i zmianą średniej prędkości, spadki ciśnienia spowodowane wszelkimi stratami i przyrosty ciśnienia wywołane pracą pomp.

Wszelkie te wielkości łatwo jest obliczyć z równania Bernoulliego obejmującego straty i dostarczenie energii przez pompy.

Dla przepływów cieczy stosujemy często określenia ciśnienia w jednostkach wysokości słupa cieczy przepływającej rurociągiem, wtedy rzędne na wykresie mają wymiar liniowy. Rzędne te odpowiadają wysokościom słupów cieczy w otwartych rurkach pionowych, które możemy przyłączyć do przewodu we wszystkich interesujących punktach. Takie rurki do pomiaru ciśnienia (nadciśnienia) nazywa się piezometrami.

Stąd wykres ciśnień wyrażony w jednostkach wysokości słupa cieczy, której przepływ badamy, nazywamy wykresami piezometrycznymi, lub linią piezometryczną. Na wykresie tym mogą występować wzrosty ciśnienia wywołane powiększeniem przekroju lub obniżeniem osi przewodu.

3. Schemat stanowiska pomiarowego:

4. Tabela pomiarów:

Punkty	Ciśnienie	Długość	Średnica
pomiarowe	[mmH2O]	[mm]	[mm]
1	295	250	36
2	245	955
3	91	1515	60
4	90	2155
5	75	2880	76
6	73	3395

5. Tabela obliczeń:

Punkty	Ciśnienie	Z uwzględnieniem
Pomiarowe	[Pa]	Patm.
1	2893,95	490,50
2	2403,45	151,74
3	892,71	99,81
4	882,9	47,15
5	735,75	39,62
6	716,13	28,48

p_atm = 637,65 [Pa]

6. Dane do wykresu:

Długość	Straty dośw.
[m]	[Pa]
0	857,30
0,256	366,80
0,955	215,06
1,515	115025,00
2,155	68,10
2,88	28,48
3,395	0,00

7. Obliczanie strat:

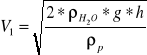
V₁ = 68,71 [m/s]

V₂ =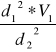

V₂ = 24,74 [m/s]

V₃ =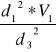

V₃ = 15,42 [m/s]

Obliczam λ

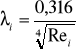
Obliczam Δp

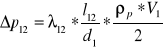
λ₁ = 0,016 Δp₁₂ = 888,71

λ₂ = 0,018 Δp₂₃ = 71,28

λ₃ = 0,019 Δp₃₄ = 18,66

8. Odczytuję ξ z tablic:

na wlocie ξ = 0,3

na pierwszym przewężeniu ξ = 0,21

na drugim przewężeniu ξ = 0,13

Obliczam straty ciśnienia na zmianach:

p_{st 1} = 868,19

p_{st 2} = 78,76

p_{st 3} = 18,94

Prędkości	Liczba	λ	Δp	ξ	pst
v [m/s]	Re		[Pa]		[Pa]
68,71	164902,23	0,016	88,71	0,3	868,19
24,74	98941,34	0,018	71,28	0,21	78,76
15,42	78111,58	0,019	18,66	0,13	18,94

9. Dane do wykresu: ciśnienie ze stratami.

Długość	Ciśnienie z strat.
[m]	[Pa]
0	Δp01 λ 0,88871
0,256	Δp12 ξ 0,86819
0,955	Δp23 λ 0,07876
1,515	Δp34 ξ 0,07128
2,155	Δp45 λ 0,01894
2,88	Δp56 ξ 0,01866

10. Wykres piezometryczny:

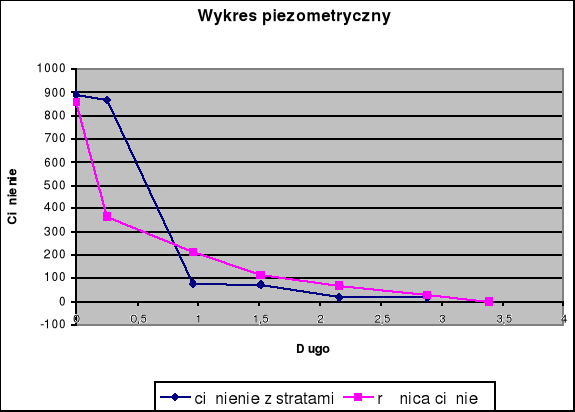
11. Wnioski:

Wykres piezometryczny, który wyszedł z obliczeń jest zgodny z literaturą. Wnioskować zatem możemy, że obliczone wartości są poprawne, a doświadczenie przeprowadzone było właściwie.

---