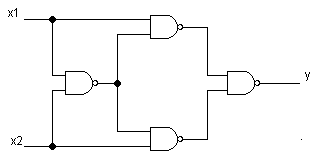
3. Poniższy układ realizuje funkcję boolowską y:
WYŻSZA SZKOŁA HANDLOWA W RADOMIU
WYDZIAŁ INFORMATYKI
STUDIA DZIENNE
SEM. 3
ZALICZENIE PRZEMIOTU:
„UKŁADY LOGICZNE”
Grupa A
Przeprowadzić konwersję kodów D/H (dziesiętny na heksadecymalny) i D/BCD (dziesiętny na BCD) liczby 415.
Który zapis przedstawia liczbę (44)10? Próby wykonaj na piśmie.
a) (2C)16
b) (00101100)2
c) (54)8
d) (1000100)BCD

3. Poniższy układ realizuje funkcję boolowską y:
a) x1x2
b) x1
2
c) x1x2+
1x2
d) x1
2+
1x2
Opisz sposób wyznaczania szukanej funkcji. Wstaw na schemacie wartości funkcji w różnych miejscach.
Korzystając z metody Karnaugha określić minimalną postać funkcji logicznej opisanej następującą tablicą:
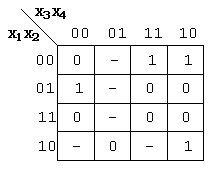
wyznacz postać koniunkcyjną funkcji (iloczynową)
wyznacz postać alternatywną funkcji (sumacyjną)
Przeprowadzić minimalizację funkcji y(x1x2x3x4)= Σ[0,1,2,3,8,9,10,11] metodą Quine'a McCluskey'a i sprawdzić, którą przyjmie postać:
a) y=x1
2+x4
b) y=x2+
1x4
c) y=x1+x2
d) y=
2
Korzystając z tablicy trójkątnej znaleźć pary zgodne (niesprzeczne) i zminimalizować automat sekwencyjny opisany następującą tablicą przejść/wyjść:
WYŻSZA SZKOŁA HANDLOWA W RADOMIU
WYDZIAŁ INFORMATYKI
STUDIA DZIENNE
SEM. 3
ZALICZENIE PRZEMIOTU:
„UKŁADY LOGICZNE”
Grupa B
Znaleźć liczbę dziesiętną odpowiadającą liczbie heksadecymalnej 4C2H, a następnie określić jej zapis w kodzie BCD (dwójkowo-dziesiętnym).
Liczba (111)10 to inaczej:
a) (157)8
b) (06F)16
c) (1101111)2
d) (1011101)2
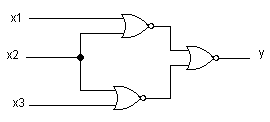
Poniższy układ realizuje funkcję boolowską y:
a) (x1+x2)(x2+x3)
b) x1+x2(x1+x3)
c) x1x2+x3x2
d) (x1+x2)x3
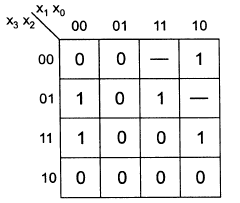
Korzystając z metody Karnaugha określić minimalną postać funkcji logicznej opisanej następującą tablicą:
wyznacz postać koniunkcyjną funkcji (iloczynową)
wyznacz postać alternatywną funkcji (sumacyjną)
Funkcja y=
[0,2,6,8,10,14]x1x2x3x4 po minimalizacji metodą Quine'a McCluskey'a przyjmie postać:
a) y=x3
4+x2
1
b) y=x3
4+
2
4
c) x1
4+x3
2
d)
3x4+x3
4
Korzystając z tablicy trójkątnej znaleźć pary zgodne (niesprzeczne) i zminimalizować automat sekwencyjny opisany następującą tablicą przejść/wyjść:
Ait\x
Ait+1
y
x
St+1