FIZYKA 1

MECHANIKA. Ruch prostoliniowy

Zasady ruchu

Ciało porusza się ruchem jednostajnym, jeśli nie działa na nie żadna siła lub działają siły równoważące się.

Ciało porusza się ruchem jednostajnie przyspieszonym, jeśli działa nań stała siła.

Przypomnienie podstawowych pojęć:

Siła F=ma, gdzie m- masa [kg]; a - przyspieszenie [m/s²].

Przyspieszenie - pochodna prędkości, a=dv/dt

Prędkość - pochodna drogi, v=dD/dt

Droga - odległość między dwoma punktami, zmienna niezależna.

Przykład

Siła spadającego ciała o masie 100 kg przy przyspieszeniu ziemskim a=g=9,81 m/s² wynosi F=981 N (Niewtonów). Ciało takie nabiera prędkości rosnącej z kwadratem czasu. Energia uderzenia o ziemię po czasie 1s wynosi:

E=mv²/2, v=∫adt=9,81 m/s, stąd E=50 [kg] x 9,81² [m/s]²≈5kJ [Jouli]. 1J=1Ws.

Jest to energia odpowiadająca w przybliżeniu działaniu grzejnika o mocy 1 kW przez 5 sekund. Energia uderzenia po 2 sekundach wzrasta czterokrotnie, do ~20 kJ itd.

Analiza ruchu samochodowego

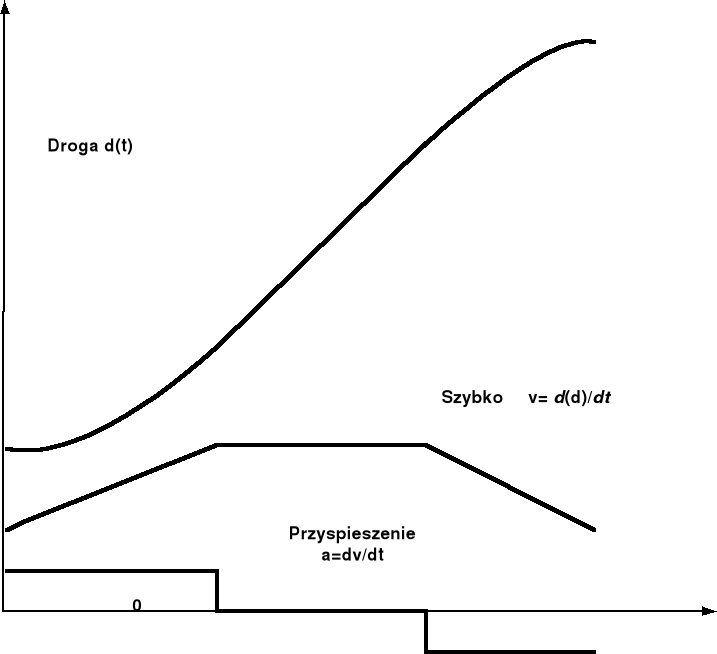
Rys.1. Typowy przebieg drogi, prędkości i przyspieszenia przy jeździe samochodem

Krzywe droga-czas nazywamy trajektoriami. Typowa trajektoria ruchu samochodu ma kształt S.

Na początku drogi samochód rozpędza się. Wobec stałej siły ciągu (stałe położenie pedału gazu) ruch jest jednostajnie przyspieszony, czyli prędkość wzrasta wg krzywej 2-go stopnia.

Po pewnym czasie następuje ruch jednostajny: droga wzrasta liniowo z czasem, prędkość jest stała, przyspieszenie a=0. Siły tarcia/oporów powietrza są równoważone niewielką siłą napędową

Na końcu drogi następuje zatrzymanie. Na samochód działa wówczas stała siła hamowania i droga zmniejsza się znów wg krzywej 2-go stopnia, prędkość maleje liniowo, a przyspieszenie (ujemne) jest stałe . Obrazuje to rys.1.

Ćwiczenie

Posługując się pojęciami, jak wyżej, wyznaczyć trajektorie ruchu 2 pojazdów o różnych opóźnieniach w procesie hamowania i określić energie kolizji w zależności od szybkości jazdy, odstępu między pojazdami, jakości układu hamulcowego oraz czasu jego reakcji na światła stopu

Przykładową ilustrację dano na rys.2 dla v=30m/s, O=30m, Δt=0 s, a₁=6 m/s², a₂=3 m/s² .

Jak wynika z szacunków graficznych kwadrat różnicy szybkości wynosi 100 j [m/s]².

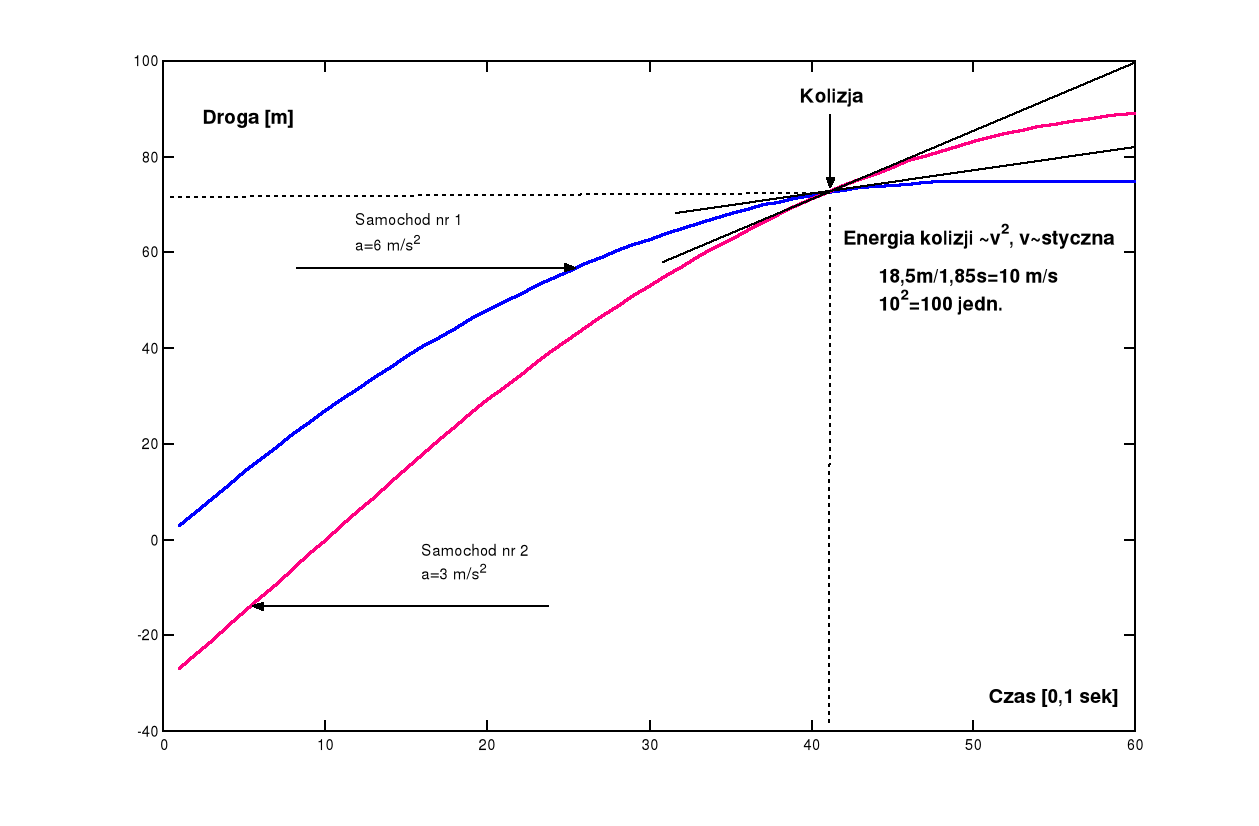
Rys.2. Trajektorie dwu hamujących samochodów o różnym przyspieszeniu ujemnym

PROGRAM

%Pojazd porusza się ruchem jednostajnie opóźnionym (a), jeśli działa nań stała siła

%Prędkość w takim ruchu maleje liniowo, bo dV/dt=a=const.

%Droga x zmniejsza się wg krzywej 2-go stopnia, bo dx/dt=V

%Równanie ruchu x(t) ma postać:x=V*t-a/2*t^2, gdzie a - opóźnienie, t^2 oznacza kwadrat

% Niech x=droga;t=czas;a=6 m/s^2

close all;clear all;

for t=1:6, x(t)=30*t-3*t^2;end;

figure;plot(x);

x2(1)=3-0.03;

for i=2:60, x2(i)=3*i-0.03*i^2; if x2(i)<x2(i-1) x2(i)=x2(i-1);end;end;

figure;plot(x2);

%Badanie wpływu prędkości i odstępu

v=3;d=30;x3(1,1)=v-0.01*v;

x3(1,2)=v-0.005*v-d;

for i=2:60,x3(i,1)=v*i-0.01*v*i^2; if x3(i,1)<x3(i-1,1) x3(i,1)=x3(i-1,1);end;

x3(i,2)=v*i-0.005*v*i^2-d;

end;

figure;plot(x3);

%Badanie wpływu reakcji kierowcy

v=3;d=30;c=15;x4(1,1)=v-0.01*v;x4(1,2)=v-0.01*v-d;

for i=2:60, x4(i,1)=v*i-0.01*v*i^2;if x4(i,1)<x4(i-1,1) x4(i,1)=x4(i-1,1);end;

if i<=c j=0;else j=i-c;end;

x4(i,2)=v*i-0.01*v*j^2-d;end;

figure;plot(x4);

%Zadanie:

%Wyznaczyć, drogą serii eksperymentów, zależność parametrów kolizji od V, odstępu d,

%opóźnienia a (jakości układu hamowania) oraz czasu reakcji kierowcy c.

%Wynikiem analizy jest kwadrat różnicy prędkości, proporcjonalny do energii zderzenia

%Dodatkowo można określać czas kolizji i długość drogi hamowania.

%Różnicę prędkości można szacować według kąta między iniami ruchu w punkcie kolizji. %Dopuszczalne jest ocena graficzna. Zmienne v,a,c d powinny się wahać plus-minus 50%

---