Wykład 1
Kinematyka punktu
1.1 Pojęcia podstawowe
MECHANIKA (OGÓLNA) - jest nauką badającą ogólne prawa ruchu obiektów materialnych (ciał) i ich wzajemne oddziaływania. Mechanikę ogólną dzielimy na: STATYKĘ, KINEMATYKĘ i DYNAMIKĘ
Obiekty materialne - wyidealizowane schematy ciał rzeczywistych. Wyróżniamy:
- punkt materialny ( w skrócie PM),
- układ punktów materialnych (UPM),
- ciało sztywne (CS).
Ruch - zjawisko zmiany położenia ciała względem innego ciała uznanego umownie za nieruchome. Nieruchome ciało nazywamy ciałem odniesienia. Wniosek: ruch jest względny tzn. zależy od wyboru ciała odniesienia.
Czas - jest w mechanice klasycznej (Newtona) pojęciem pierwotnym i absolutnym. Czas nie zależy od wyboru układu odniesienia i jest taki sam w każdym punkcie przestrzeni. Przyjmuje się, że czas jest stale nieujemny t ≥ 0 i występuje tylko wtedy gdy występuje ruch.
Układ odniesienia - jest to układ współrzędnych sztywno związany z ciałem odniesienia, który służy do opisu ruchu obiektu (-ów).
Oxyz - układ odniesienia, prostokątny prawoskrętny układ współrzędnych
1.2 Kinematyka punktu w układzie Oxyz
Kinematyka - jest to dział mechaniki, w którym bada się ruch obiektów bez wnikania w przyczyny wywołujące ten ruch. Można ją nazwać geometrią ruchu, bowiem do opisu tego ruchu stosujemy pojęcia przestrzeni i czasu.
Wielkości fizyczne w kinematyce:
1. Droga, przesunięcie, przemieszczenie - [translacja - m, obrót - rad ]
2. Prędkość - [m/s, rad/s]
3. Przyspieszenie - [m/s2, rad/s2]
4. Tor ruchu punktu - równanie krzywej, po której następuje ruch tego punktu, np.:
y = y(x) y = 3x2 - 6x + 5
Opis ruchu punktu:
Matematycznie ruch punktu opisujemy w postaci wektorowej lub skalarnej. Opisy te są równoważne.
Równanie wektorowe ruchu: ![]()
Równania skalarne w układzie Oxyz: x=x(t), y=y(t), z=z(t)
Prędkość punktu w Oxyz:
![]()
Moduł wektora prędkości jest wartością prędkości. NIE MYLIĆ pojęć wektora prędkości i jej wartości!
![]()
przy czym ![]()
Wartość prędkości (długość wektora):
![]()
Przyspieszenie punktu w Oxyz:
![]()
UWAGA: wektor przyspieszenia punktu ma na ogół inny kierunek niż wektor prędkości!
Wektor przyspieszenia i jego współrzędne:
![]()
![]()
, ![]()
, ![]()
Wartość przyspieszenia (długość wektora):
![]()
1.3 Kinematyka punktu w układzie naturalnym:
Założenia:
- Ruch punktu jest dany w postaci: ![]()
; gdzie s= s(t)
- Początek układu współrzędnych jest związany z ruchomym punktem A na torze.
Układ taki nazywamy naturalnym lub trójścianem Freneta.
Prędkość punktu w układzie naturalnym:
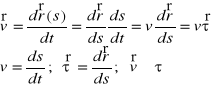
Przyspieszenie punktu w układzie naturalnym:
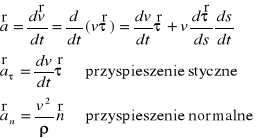
ρ - promień krzywizny toru w punkcie A.
Moduł i współrzędne wektora przyspieszenia w układzie naturalnym:
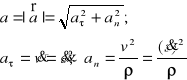
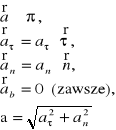
Wyszukiwarka
Podobne podstrony:
5439
5439
05 10id 5439 Nieznany (2)
5439
5439
5439
więcej podobnych podstron