PRZYKŁADY - OCENA PROJEKTÓW
Oblicz stopę zwrotu, jeśli PV wynosi 300, FV 800, a okres inwestycji to 5 lat.
![]()
Nakłady początkowe inwestycji wyniosły 2000 PLN. Na zakończenie kolejnych lat projekt przyniósł następujące przypływy: 500, 800, 200, 900. Jaka jest wartość bieżąca netto dla tej inwestycji, jeśli stopa procentowa wynosi 7% p.a.?
![]()
Nakłady początkowe inwestycji wyniosły 1000 PLN. Na zakończenie kolejnych lat projekt przyniósł następujące przypływy: 100, 800, 300. Jaka jest wartość bieżąca netto dla tej inwestycji, jeśli stopa procentowa w poszczególnych latach wynosiła 3%, 9%, 11%?
![]()
Przepływy pieniężne: 500, 1800, 500.
Nakład inwestycyjny: 2000.
Stopa dyskontowa: 7%.
Ile wynosi IRR dla tego projektu i czy jest on ekonomicznie uzasadniony?
![]()
IRR = 0.186303
inwestycja jest uzasadniona, gdyż IRR = 19% > r = 7%
NPV = 447,63
Mamy do wyboru 2 projekty, które można zrealizować w tym samym okresie:
A: przepływy: -80, 120, 300
B: przepływy: -400,750, 1300
Wymagana stopa zwrotu wynosi 13%.
Ocenić projekty z punktu widzenia PI.
Projekt A: 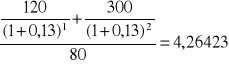
Projekt B: 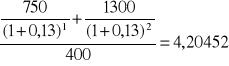
zgodnie ze wskaźnikiem rentowności do realizacji wybrany zostanie projekt A
Prosty okres zwrotu
Przepływy pieniężne: -1000, 700, 200, 300.
Skumulowana gotówka netto: -1000, -300, -100, 200.
Okres zwrotu jest więc dłuższy niż 2 lata i krótszy niż 3.
Wyznaczamy go w następujący sposób: PP = 2 + 100 / 300 = 2,33 roku
Po tym okresie zacznie być tworzona nadwyżka dla inwestora.
Zdyskontowany okres zwrotu
Dane jak powyżej.
Załóżmy, że stopa dyskontowa wynosi 10%.
Zdyskontowana gotówka netto: -1000, 636.36, 165.29, 225.39.
Zdyskontowana skumulowana gotówka netto: -1000, -363.64, -198.35, 27,04.
Okres zwrotu jest więc dłuższy niż 2 lata i krótszy niż 3.
Wyznaczamy go w następujący sposób: PP = 2 + 198.35 / 225.39 = 2,88 roku
Po tym okresie zacznie być tworzona nadwyżka dla inwestora.
Zdyskontowany okres zwrotu jest więc dłuższy od prostego okresu zwrotu.
1
2
Wyszukiwarka
Podobne podstrony:
Ocena projektów inwestycyjnych-wzory, STUDIA, UG I stopień, UG FiR (II rok), Semestr IV, Finanse prz
ocena projektow inwestycyjnych
ocena projektów inwestycyjnych(11 str), Ekonomia, ekonomia
ocena projektow inwestycyjnych - zadania
ocena projektów inwestycyjnych(11 str), Bankowość i Finanse
2 Ocena projektów inwestycyjnychwww
Ocena projektów inwestycyjnych (28 stron), I
ocena projektow inwestycyjnych
Ocena efektywności projektów inwestycyjnych 2014 01 12 zadania
INW CRIB, Ocena ekonomiczno-finansowa projektów inwestycyjnych
INW02 , Ocena ekonomiczno-finansowa projektów inwestycyjnych
Ocena efektywności projektów inwestycyjnych 2013 12 22 zadania
więcej podobnych podstron