Radosław Paliszkiewicz
Wydział: Informatyka i Zarządzanie
Kierunek: Informatyka
Rok II, semestr III
Data pomiarów: 8.10.1997
Sprawozdanie numer 1
Ćwiczenie 59: Badanie propagacji mikrofal.
1. Pomiar charakterystyki kierunkowej tuby nadawczej.
W ćwiczeniu tym badana była zależność mocy mikrofali emitowanej z tuby nadawczej od kąta ustawienia tuby odbiorczej. Moc ta odczytywana była pośrednio przez wskazania woltomierza. Czym wyższe były wskazania woltomierza - tym większa moc fali.
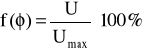
Wynik pomiaru przedstawiony zostanie graficznie w postaci wykresu funkcji we współrzędnych biegunowych
przy czym Umax przyjmiemy jako równe 1.
1.1. Schemat układu pomiarowego.
Do wejścia tuby nadawczej N podłączono klistron generujący mikrofale, do wyjścia tuby odbiorczej O - woltomierz cyfrowy V530. Pomiar polega na odczycie wskazań woltomierza w zależności od zmiany kąta podczas obrotu tuby odbiorczej, przy ustalonej odległości między tubami r.
1.2. Wyniki pomiarów.
Lp. |
|
U1 |
U1 |
δU1 |
U2 |
U1 |
δU2 |
UŚR |
|
[deg] |
[mV] |
[mV] |
[%] |
[mV] |
[mV] |
[%] |
[mV] |
1 |
0.00 |
19.20 |
0.02 |
0.11 |
19.20 |
0.02 |
0.11 |
19.20 |
2 |
2.50 |
20.10 |
0.03 |
0.15 |
19.40 |
0.02 |
0.11 |
19.75 |
3 |
5.00 |
21.80 |
0.03 |
0.14 |
18.50 |
0.02 |
0.11 |
20.15 |
4 |
7.50 |
25.50 |
0.03 |
0.12 |
18.50 |
0.02 |
0.11 |
22.00 |
5 |
10.00 |
26.60 |
0.03 |
0.12 |
18.20 |
0.02 |
0.11 |
22.40 |
6 |
12.50 |
22.80 |
0.03 |
0.14 |
17.00 |
0.02 |
0.12 |
19.90 |
7 |
15.00 |
19.90 |
0.02 |
0.11 |
14.70 |
0.02 |
0.14 |
17.30 |
8 |
17.50 |
14.80 |
0.02 |
0.14 |
12.80 |
0.02 |
0.16 |
13.80 |
9 |
20.00 |
10.40 |
0.02 |
0.20 |
10.50 |
0.02 |
0.20 |
10.45 |
10 |
22.50 |
8.50 |
0.02 |
0.24 |
8.00 |
0.02 |
0.25 |
8.25 |
11 |
25.00 |
6.50 |
0.02 |
0.31 |
6.00 |
0.02 |
0.34 |
6.25 |
12 |
27.50 |
4.80 |
0.02 |
0.42 |
4.40 |
0.02 |
0.46 |
4.60 |
13 |
30.00 |
4.50 |
0.02 |
0.45 |
3.50 |
0.02 |
0.58 |
4.00 |
14 |
32.50 |
2.80 |
0.02 |
0.72 |
2.60 |
0.02 |
0.80 |
2.70 |
15 |
35.00 |
1.90 |
0.02 |
1.10 |
2.10 |
0.02 |
1.00 |
2.00 |
16 |
37.50 |
1.00 |
0.02 |
2.00 |
1.50 |
0.02 |
1.40 |
1.25 |
17 |
40.00 |
0.70 |
0.02 |
3.00 |
1.00 |
0.02 |
2.00 |
0.85 |
18 |
42.50 |
0.60 |
0.02 |
3.40 |
0.60 |
0.02 |
3.40 |
0.60 |
19 |
45.00 |
0.30 |
0.02 |
7.00 |
0.30 |
0.02 |
7.00 |
0.30 |
1.3. Prezentacja graficzna kierunkowej charakterystyki tuby nadawczej.
2. Wyznaczania długości fali z rozkładu amplitudy fali stojącej.
W tym pomiarze zamiast z tuby odbiorczej wykorzystano detektor punktowy, również podłączony do woltomierza. Na pomiar składają się odczyt kolejnych maksimów wskazań woltomierza przy przesuwaniu głowicy detektora w kierunku tuby nadawczej wraz z odczytem odległości od tuby odczytywanej na ramieniu po którym porusza się detektor. Odległości między poszczególnymi maksimami są równe połowie długości mikrofali.
2.1. Układ pomiarowy.
Układ składa się z nieruchomej tuby nadawczej N i poruszającego się detektora punktowego D. Do tuby podłączono klistron generujący mikrofale, do detektora woltomierz cyfrowy V530. Za detektorem umieszczono płytę metalową spełniającą rolę zwierciadła
2.2. Wyniki pomiarów
Lp |
U |
l |
|
[mV] |
[cm] |
1 |
0.27 |
52 |
2 |
0.33 |
49 |
3 |
0.30 |
46 |
4 |
0.28 |
43 |
5 |
0.30 |
40 |
Zatem długość fali wynosi 6 cm - podwojona odległość między punktami maksymalnych wskazań.
3. Dyskusja błędów.
3.1. Błędy systematyczne.
W przypadku pomiaru pierwszego możemy obliczyć błąd systematyczny wynikający z klasy przyrządu, który był wykorzystywany w pomiarach. Dokładność podstawowa tego woltomierza wynosi 0.05% zmierzonej wartości, zaś błąd dyskretyzacji wynosi 0.01% podzakresu. Bezwzględny błąd dyskretyzacji jest stały dla wszystkich pomiarów(pomiary wykonywane były dla jednego podzakresu) i wynosi ±(100mV * 0.01%) = ± 0.01mV.
Wprowadźmy oznaczenia:
X - wynik pomiaru
Z = 100 mV- podzakres, na którym dokonywane były pomiary
k - całkowity błąd bezwzględny wynikający z klasy
δd = 0.01%*Z - względny błąd dyskretyzacji
δp = 0.05%*X - względny błąd podstawowy.
Dla przykładowych pomiarów /pomiar nr 13 i 2/ mamy:
X1=4.50 mV, X2=3.50 mV
Mamy więc:
Wyniki błędów należało zaokrąglić do góry do setnej części mV, gdyż taką dokładność odczytu daje nam woltomierz V530. Można teraz obliczyć dokładność tych dwóch pomiarów (cały czas mowa o dokładności i błędzie wynikającym z klasy, nie zaś o przypadkowym).
Jak widać większy pomiar miał większą dokładność, chociaż jego błąd bezwzględny był większy niż przy pomiarze mniejszym. Wyniki obliczeń wszystkich błędów względnych zawiera tabelka.
3.2. Błędy przypadkowe
Ilość wykonanych pomiarów uniemożliwia prawidłową ocenę zarówno popełnionych błędów przypadkowych, jak i prawidłowych wyników pomiarów. Dodatkowy problem stwarzają warunki wykonywania pomiarów - wadliwie zachowujący się miernik, którego włączanie i wyłączanie zabierało większą część czasu poświęconego pomiarom.
Możliwe jest jednak obliczenie średniej wartości pomiaru, niepewność oraz niepewność względną j-tego pomiaru, przyjmując, że seria składała się z dwóch pomiarów.
Wprowadźmy oznaczenia:
j = Xj - XŚR - niepewność j-tego pomiaru
δj = - niepewność względna j-tego pomiaru.
Możemy obliczyć te wartości np. dla 10-tego pomiaru:
X1 = 8.50 mV , X2=8.00 mV, XŚR=8.25 mV.
1 = 8.50 - 8.25 = 0.25 mV
2 = 8.00 - 8.25 = - 0.25 mV
δ1 = 0.25*100/8.25 = 3.1 %
δ2 = - 0.25*100/8.25 = - 3.1 %.
Ponieważ dla naszej serii dwóch pomiarów wartości poszczególnych pomiarów są równoodległe od wartości średniej nie ma sensu obliczać pozostałych błędów.
4. Wnioski
Wyniki badań są generalnie zgodne z modelem, za wyjątkiem odchyłu mocy fali emitowanej z tuby nadawczej przy kątach do 15º. Odchył ten spowodowany był prawdopodobnie nagromadzeniem w laboratorium metalowych sprzętów, zmieniających bieg mikrofal oraz wadliwym działaniem woltomierza. W przypadku drugiego pomiaru, podczas którego wybitnie dawał się we znaki woltomierz potwierdziły się oczekiwania co do długości fali. Niestety badanie przeprowadzone było tylko raz, w związku z czym nie można jednak mówić o jego wiarygodności. Była to raczej obserwacja, niż prawdziwy pomiar.
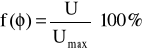
O
N
r
![]()

N
![]()
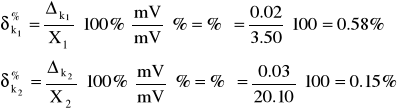
![]()
M
D
Wyszukiwarka
Podobne podstrony:
CWI59C(1), Politechnika Wrocławska - Materiały, fizyka 2, paczka 1, 59
CWI59F(1), Politechnika Wrocławska - Materiały, fizyka 2, paczka 1, 59
Spraw1(1), Politechnika Wrocławska - Materiały, fizyka 2, paczka 1, piknometr
sprawko8dobre(1), Politechnika Wrocławska - Materiały, fizyka 2, paczka 2, sprawko 8
Fizyka lab. cw77(1), Politechnika Wrocławska - Materiały, fizyka 2, paczka 1, fizyka-lab
Cw11, Politechnika Wrocławska - Materiały, fizyka 2, paczka 1, 11 modul younga predkosc dzwieku
Fizyka lab.cw24(1), Politechnika Wrocławska - Materiały, fizyka 2, paczka 1, fizyka-lab
Fizyka lab.cw8(1), Politechnika Wrocławska - Materiały, fizyka 2, paczka 1, fizyka-lab
więcej podobnych podstron