ALGEBRA LINIOWA

Ciało liczb zespolonych- są to wszystkie liczby zespolone wraz ze wszystkimi działaniami jakie można na nich wykonać(dodawanie, odejmowanie, mnożenie, dzielenie)

Zasadnicze twierdzenie algebry- każdy wielomian zespolony stopnia drugiego ma przynajmniej jeden pierwiastek zespolony

Moduł liczby zespolonej- odległość punktu od środka ukł współrzędnych

Argument liczby zespolonej- kąt zawarty pomiędzy dodatnią częścią osi x ukł współrzędnych a promieniem wodzącym

Liniowa niezależność- skończony układ wektorów w przestrzeni liniowej V nazwiemy ukł liniowo niezależnym gdy każda kombinacja liniowa wektorów daje wektor niezerowy.

Baza- maksymalny zbiór wektorów liniowo niezależnych w przestrzeni.

Rząd macierzy- jest równy ilości liniowo niezależnych wierszy lub kolumn w macierzy

Mnożenie macierzy (A*B)- możliwe jest wtedy i tylko wtedy gdy liczba wierszy macierzy A jest równa liczbie kolumn macierzy B.

Macierz A jest odwracalna, jeśli istnieje taka macierz B, dla której

AB = BA = I, gdzie I jest macierzą jednostkową.

Twierdzenie Kroneckera-Capellego

Niech n będzie liczbą niewiadomych ukł, r rzędem macierzy głównej, s rzędem macierzy rozszerzonej. O współczynnikach układu zakładamy że należą do nieskończonego ciała liczbowego.

Układ równań liniowych ma rozwiązanie wtedy i tylko wtedy gdy r=s. Jeżeli zachodzi dodatkowo r=s=n, to taki układ ma dokładnie jedno rozwiązanie. Jeśli zaś r=s<n to ukłąd ma nieskończenie wiele rozwiązań zależnych od n-r parametrów; zbiór tych rozwiązań tworzy n-r wymiarową podprzestrzeń przestrzeni n-wymiarowej jeśli układ jest jednorodny. Przypadek r>n jest niemożliwy

Układ Cramera- to układ kwadratowy spełniający warunek detA=/0. Jednorodny układ Cramera ma tylko rozwiązanie zerowe w postaci x1=x2....xn=0. Rozwiązanie to określone jest poprzez tzw wzory Cramera:

x1=detA1/detA …. xn=detAn/detA

ANALIZA MATEMATYCZNA

Twierdzenie o trzech ciągach mówi, że jeśli dane są trzy ciągi liczb rzeczywistych an, bn i cn takie, że dla prawie wszystkich n

oraz

wówczas

Pochodna- przyrost wartości funkcji do przyrostu argumentu.

Interpretacja geometryczna pochodnej- Pochodną funkcji na przedziale można uważać za liczbową charakterystykę szybkości wzrostu danej funkcji (duża pochodna - stromy wykres, niewielka pochodna - wykres łagodnie wznoszący się, ujemna pochodna - wykres opadający itp.).

Różniczka - ciągłe odwzorowanie liniowe przybliżające lokalnie wartości danej funkcji w otoczeniu ustalonego punktu.

Twierdzenie Lagrange'a-Jeśli dana funkcja

jest

ciągła w przedziale [a,b],

różniczkowalna w przedziale (a,b),

to istnieje taki punkt ,

że:

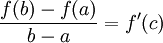
Twierdzenie nie zachodzi w przypadku wielowymiarowym.

Liczba Eulera(e)-

Wzór Taylora:

Niech Y będzie przestrzenią unormowaną. Załóżmy, że f: [a,b] ---> Y jest (n+1)-razy różniczkowalna na [a,b] w sposób ciągły. Wówczas dla każdego x należy (a,b)

gdzie Rn(x,a) spełnia warunek

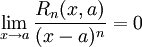
Regula l'Hospitala:

Bezpośrednio z definicji pochodnej funkcji można wykazać następujące twierdzenie:

Jeżeli funkcje f i g są określone w przedziale otwartym zawierającym punkt a oraz

1.

2.

3. istnieją (skończone) pochodne f'(a)i g'(a),przy czym g'(a) jest różne od 0.

Wówczas

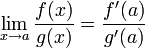
Ekstremum- najmniejsza lub największa wartość funkcji.

Warunek konieczny istnienia ekstremum lokalnego funkcji f w pewnym punkcie x0należącym do (a,b) to f'(x0)=0

Punkt przegięcia jest w analizie matematycznej punktem na wykresie funkcji, w którym zachodzi zmiana jej wypukłości, tj. funkcja wypukła na lewo od tego punktu staje się wklęsła na prawo od niego lub na odwrót. Pojęcie to może być też uogólnione na inne krzywe.

Warunkiem wystarczającym istnienia punktu przegięcia jest też istnienie drugiej pochodnej funkcji równej zeru w punkcie x0, oraz zmiana jej znaku w tym punkcie. Jeżeli funkcja ma zerową drugą pochodną w punkcie, ale jej znak nie zmienia się w tym punkcie, to funkcja ma w tym punkcie ekstremum lokalne.

Całkowanie przez części- metoda ta wynika ze wzoru na pochodną iloczynu:

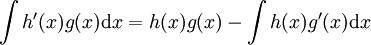
Całkowanie przez podstawianie-

Całka Riemanna- Całkę funkcji f można opisać jako liczbę otrzymaną w wyniku następującego procesu:

1. Bierzemy pod uwagę dowolny podział przedziału [a,b] punktami na przedziały [ti,ti + 1]; następnie w każdym z takich przedziałów obieramy dowolnie punkt ξi.

2. Obliczamy wszystkie iloczyny f(ξi)(ti + 1 − ti)

3. Sumujemy tak obliczone wielkości

4. Przechodzimy do granicy ze względu na N dążące do nieskończoności oraz ze względu na maksymalną długość przedziału [ti,ti + 1] dążącą do zera; jeśli granica ta istnieje, to ona właśnie jest szukaną całką funkcji f w sensie Riemanna.

Łatwo zauważyć, że w przypadku funkcji o wartościach dodatnich, geometrycznie powyższa procedura oznacza przybliżanie pola powierzchni pod krzywą sumą pól pewnych prostokątów; jeśli przybliżenia te są zbieżne, to właśnie granicę owej sumy nazywamy całką Riemanna. Przedstawiony tu opis, a ściślej mówiąc przejście graniczne opisane w punkcie czwartym, wymaga pewnej formalizacji.

Całka Newtona-Leibniza- funkcji f na przedziale domkniętym [a;b] jest określona jako F(b) - F(a), gdzie F jest dowolną funkcją pierwotną funkcji f określoną na tym przedziale.

Istnienie całki Newtona-Leibniza danej funkcji f jest więc równoznaczne z istnieniem funkcji pierwotnej. Ponieważ każde dwie funkcje pierwotne różnią się o stałą, więc różnica F(b) - F(a) nie zależy od wyboru konkretnej funkcji pierwotnej F.

Funkcję f nazywamy całkowalną w sensie Newtona-Leibniza, jeśli ma całkę Newtona-Leibniza (czyli jeśli ma funkcję pierwotną).

Dla zastosowań ważny jest fakt, że każda funkcja ciągła na przedziale domkniętym jest całkowalna w sensie Newtona-Leibniza.

Całka niewłaściwa- ALE JA ZNAM WZÓR!!!!

Pochodne cząstkowe- Pochodna cząstkowa funkcji wielu zmiennych względem wybranej zmiennej, to "zwykła" pochodna tej funkcji obliczona przy założeniu, że pozostałe zmienne mają ustalone wartości.

Całka podwójna- całka po dwóch zmiennych z funkcji dwóch zmiennych z = f(x,y):

Całka ta ma interpretację objętości zawartej między płaszczyzną z=0 a powierzchnią z = f(x,y). Jest szczególnym przypadkiem całki wielokrotnej.

STATYSTYKA

Wartość oczekiwana (przeciętna, średnia), nadzieja matematyczna - w rachunku prawdopodobieństwa wartość opisująca spodziewany (średnio) wynik doświadczenia losowego. Wartość oczekiwana to inaczej pierwszy moment zwykły. Estymatorem wartości oczekiwanej rozkładu cechy w populacji jest średnia arytmetyczna.

Wariancja to w statystyce klasyczna miara zmienności. Intuicyjnie utożsamiana ze zróżnicowaniem zbiorowości; jest średnią arytmetyczną kwadratów odchyleń (różnic) poszczególnych wartości cechy od wartości oczekiwanej.

Wariancja zmiennej losowej X zdefiniowana jest wzorem:

,

gdzie jest wartością oczekiwaną zmiennej losowej. Innym, często prostszym sposobem wyznaczania wariancji jest wzór: D2(X) = E(X2) − [E(X)]2.

Jakie warunki musi spełniać funkcja gęstości zmiennej typu ciągłego?

Funkcja f(x) spełnia następujące warunki:

•f(x)>=0 dla każdego x∈R;

• -∞∫∞ f(x)dx=1.

Jezeli pewna funkcja f(x) spełnia te warunki, to dla pewnej ciagłej zmiennej losowej X

funkcja f(x) jest gestoscia jej rozkładu. Funkcja f ma wtedy probabilistyczna interpretacje, reprezentacje, moze byc uzywana w modelach w roli gestosci rozkładu ciagłego.

Dystrybuanta - w rachunku prawdopodobieństwa, statystyce i dziedzinach pokrewnych, funkcja rzeczywista jednoznacznie wyznaczająca rozkład prawdopodobieństwa (tj. miarę probabilistyczną określoną na σ-ciele borelowskich podzbiorów prostej[1]), a więc zawierająca o nim wszystkie informacje. Dystrybuanty są efektywnym narzędziem badania prawdopodobieństwa ponieważ, z matematycznego punktu widzenia, są obiektem prostszym niż rozkłady prawdopodobieństwa. Dystrybuanta rozkładu próby zwana jest dystrybuantą empiryczną. Jest ona blisko związana z pojęciem rangi.

Współczynnik korelacji - liczba określająca w jakim stopniu zmienne są współzależne. Jest miarą korelacji dwu (lub więcej) zmiennych. Zwykle może przybierać wartości od -1 (zupełna korelacja ujemna), przez 0 (brak korelacji) do +1 (zupełna korelacja dodatnia).

Kwantyl - Kwantylem rzędu p, gdzie 0 ≤ p ≤ 1, w rozkładzie empirycznym PX zmiennej losowej X nazywamy każdą liczbę xp, dla której spełnione są nierówności

oraz

W szczególności, kwantylem rzędu p jest taka wartość xp zmiennej losowej, że wartości mniejsze lub równe od xp są przyjmowane z prawdopodobieństwem co najmniej p, zaś wartości większe lub równe od xp są przyjmowane z prawdopodobieństwem co najmniej 1-p.

Estymatorem wartości oczekiwanej rozkładu cechy w populacji jest średnia arytmetyczna.

---